大峪河径流特性初步分析

吴丽娜,黄领梅,沈 冰

(西安理工大学 西北水资源与环境生态教育部重点实验室,西安 710048)

0 引 言

大峪河是潏河的一级支流,沣河的二级支流,渭河的三级支流,属黄河流域。大峪河发源于秦岭北麓,主河道长18.5 km,由南向北流动,主河道平均比降 33.1‰,多年平均径流量约为2 981.17×104m3,常年流量0.3 m3/s,枯水期流量0.2 m3/s。大峪河重要控制站——大峪水文站,位于E109°07′,N34°00′,距离河口14 km,集水面积53.9 km2,该站自1952年设站观测以来,至今已累积了50 a左右的观测资料。2009年2月,西安市政府决定启动大峪引水工程来解决了兴庆湖和护城河的水质问题,同时也可以解决曲江池、芙蓉湖和拟建的航天产业基地人工湖生态景观用水问题。该工程的水源位于长安区境内的大峪、东沟和许家沟3座水库,引水来自大峪河和库峪河径流。因此,大峪河作为工程水源之一,对其径流序列进行初步分析,揭示其径流变化特性及规律,将对各部门合理治理水污染、解决西安市生态景观用水具有重要的理论意义和借鉴价值。

1 径流变化趋势性分析

径流作为水文时间序列,其年际变化一般呈锯齿状高频振荡,这样就很难区分某一自然过程是处于自然波动还是确实存在特定的变化趋势[1]。水文时间序列中的趋势成分是指该序列统计参数随时间的增长而增加或减少的现象[2]。常用的趋势性统计检验法包括Kendall秩次相关检验、Spearman秩次相关检验以及线性趋势回归检验等。本文采用Kendall秩次相关检验法来检验序列是否有显著趋势。

Mann-Kendall检验法:即非参数秩次相关统计检验,它以适用范围广、人为性少、定量化程度高而著称,在水文领域中,已被应用于气候、水质、降雨量、径流量等时间序列的趋势成分研究;另外与参数统计检验法相比较,非参数检验法更适用于非正态分布,而时间序列的分布一般属于非正态分布[3]。

取显著水平α=0.05,查标准正态分布表可得到临界值Zα/2=1.96。若|Z|＞Zα/2,即在显著水平α下序列存在向下或向上的趋势,否则序列上升或下降趋势不显著;统计变量Z＞0时,表示序列存在上升趋势,Z＜0时,表示序列存在下降趋势。

大峪河1955～2006年的年径流量过程见图1。整个时间段内的平均径流量为2 981.17×104m3。径流量的最大值出现在 1983年,径流量为6 694.49×104m3;最小值出现在 2006年,径流量为1 083.15×104m3。总之,以1983年为分界线,其前后时段内径流量基本保持水平,变化不大。

图1 大峪站年径流序列过程图Fig.1 Process of annual runoff at Dayu Station

本文将1955～2006年52 a的径流量作为一个样本序列,构造统计量S后,计算统计变量-1.96＜Z=-0.915＜0,结果表明,大峪站的年径流序列存在下降趋势,但不显著。因此可以对原序列直接进行周期性分析。

2 径流周期性分析

2.1 差积曲线法

差积曲线反映了年径流量的丰、枯变化,差积曲线的形状不同表明年径流的周期不同。由大峪站年径流量差积曲线(图2)得出,年径流量在1985年出现最高点,1979年出现最低点。1955～2006年的年径流量过程大致可以分为以下几个阶段: 1955～1968年为上升段,1969～1979年为下降段, 1980～1985年为上升段,1986～2002年为下降段。

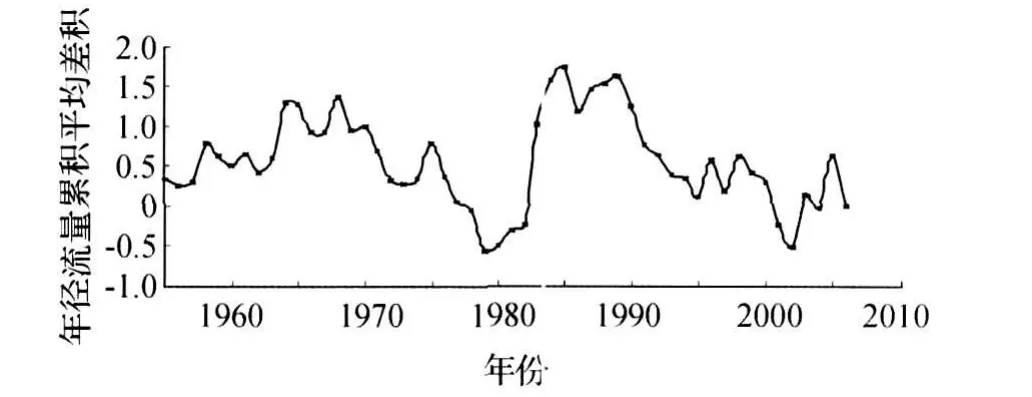
图2 年径流量模比系数差积曲线Fig.2 Annual runoff residual mass diagram of frequency factor

2.2 滑动平均法

采用滑动平均法,可以分析径流量的周期性,因为n年滑动平均值可以把＜n年的波动消除,把＞n年的周期性表示出来[4]。滑动平均值的计算公式为:

式中y′t为t点的滑动平均值;当n=1、2、3时,分别对应3点滑动平均、5点滑动平均、7点滑动平均,然后求其平均值,作为第t年的线性趋势序列。

大峪站年径流量5 a滑动平均值过程线(图3)表明,1955～2006年径流量有 2段丰水期即1955～1967,1979～1984,2段平水期即 1969～1979,1995～2006,1段枯水期即1985～1994,短周期4～8 a,长周期12～25 a;

图3 大峪站年径流与5 a滑动平均过程线Fig.3 Curve of annual runoff and 5-year moving average annual runoff at Dayu Station

3 混沌特性分析

3.1 月径流序列的相空间重构

相空间的建立不仅是混沌分析研究的前提而且是混沌时间序列预测的重要基础。对于单变量时间序列,Packard[5]等人提出了一种重构相空间的方法,将混沌理论引入到非线性时间序列分析中[6]。其主要思想在于选取恰当的延迟时间τ和嵌入维数m,把一维变量的时间序列转变成多维变量的相空间,重构原动力系统。设给定的时间序列为 x (t),t=1,2,…,N,重构相空间:

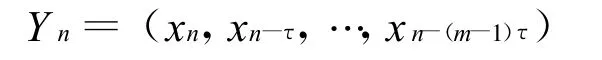
本文选择传统的自相关函数法选取延迟时间τ,它主要是通过提取时间序列间的线性相关性来求得自相关系数,一般情况下,当自相关函数随滞时衰减明显时,嵌入滞时τ可取为自相关函数第一次过零点时所对应的滞时[7]。即:

接近0时对应的k即是所求的延时τ,图4所示为大峪水文站月径流序列自相关函数图,为了保证各嵌入坐标间的相关性最小,选取月径流序列自相关函数第一次过零点时所对应的时间为重构相空间的最佳延迟时间。当k依次取1,2,…,150时,自相关函数r随k值变化,其中:r(2)=0.148 3, r(3)=-0.025 87,故选择最佳嵌入时间τ=3。

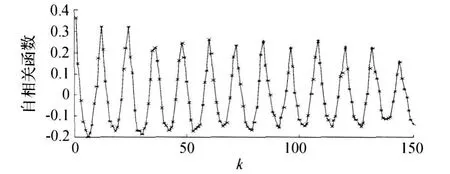
图4 自相关函数图Fig.4 Self-correlation function diagram

3.2 吸引子分维数d的计算

混沌现象识别的方法是刻画相空间中奇怪吸引子的特征,混沌特性的定量指标包括:关联维数、Lyapunov指数以及Kolomogrov熵等。本文采用关联维数法(G-P)估算吸引子分维数。

假定一个较小嵌入维m0重构相空间,取适当的距离r(r为两相点之间的距离,其取值不宜过大也不宜过小,但没有严格的选取规则,文中采用试算法确定),然后计算关联积分函数(r),对于r的某个适当范围,吸引子的维数d与累积分布函数Cm(r)应满足对数线性关系,即d(m)= ln(r)/lnr,从而由拟合求出对应于的关联维数估计值d(),增加嵌入维数直到相应的维数值d(m)不再随m值的增长而在一定的误差范围内不变为止,与之对应的m值即为最佳嵌入维数[2]。本文在确定滞时τ=3时,取m= 1,2,…,11,依次计算关联积分函数 Cm(r),作出ln(r)～lnr的关系曲线,见图5。在不同嵌入维m下,ln(r)～lnr关系图中存在直线相关的部分(即存在无标度区间),因此说明大峪站月径流序列具有明显分形特征,每一条曲线的直线段部分的斜率即为各自嵌入维数(i=1,2,…,11)所对应的关联维数d(),由此得到m～d关系图。

如图6所示,当m≥12时,曲线趋于平行 X轴,此时关联维数达到饱和,即饱和关联维数 d (12)=4.889。在降水时间序列=3,m=12的情况下,根据Wolf法计算出最大 Lyapunov指数λ1=0.177 0＞0,表明轨道按指数分离,该时间序列具有一定的混沌特性。

3.3 最大Lyapunov指数

Lyapunov指数作为混沌的一个最为重要的特征值,从整体上反映了动力系统的混沌量水平,并且混沌系统的Lyapunov指数至少有一个＞0。因此,只要计算出最大Lyapunov指数＞0即可判别其为混沌序列。文中采用Wolf方法,其主要思想是在重构相空间后,直接基于相轨线、相平面、相体积等演化来估计Lyapunov指数[5]。经计算,大峪站月径流的最大Lyapunov指数λ1=0.177 0＞0,因此,进一步说明该月径流序列具有混沌特性。

4 结 论

通过对大峪水文站径流时间序列的演变趋势分析、周期性分析以及混沌特性分析和计算,得出以下结论:

1)首先由Mann-Kendall检验法检验出大峪水文站1955～2006年的年径流序列存在下降趋势,但不显著;其次采用差积曲线法和滑动平均法对大峪站的年径流作周期性分析,结果表明,大峪站径流量年际变化不大,短周期4～8 a,长周期12～25 a;最后对大峪站月径流时间序列进行相空间重构,由于序列存在非整数饱和关联维数,并且最大Lyapunov指数＞0,因此说明大峪站月径流序列具有一定的混沌特性。

2)本文对大峪河径流序列作初步分析时存在以下问题及建议:①对于大峪河径流的减少趋势,相关部门要予以极大的关注,并制定相应的流域水资源管理对策,保证水资源量最大限度的减少给引水工程带来的不利;②对于周期性分析,本文应用的方法属于最基础的方法,所得的周期值比较组略,为了进一步了解大峪河径流序列的周期特性还应采用更加有效的方法。

[1]王现领,冯 平.滦河流域年径流量趋势分析 [J].海河水利,2010,1(2):5-6.

[2]丁 晶,邓育仁.随机水文学[M].成都:成都科技大学出版社,1988:64-110.

[3]秦年秀,姜 彤,许崇育.长江流域径流趋势变化及突变分析[J].长江流域资源与环境,2005,14(5): 590-593.

[4]段莉珠.大盈江干流径流特性浅析[J].水资源研究, 2010,31(1):10-12.

[5]吕金虎,陆君安,陈安华.混沌时间序列分析及其应用[M].武汉:武汉大学出版社,2002:46-63.

[6]黄国如,苪孝芳.流域降雨径流时间序列的混沌特性识别及其预测研究新进展 [J].水科学进展,2004,15 (2):255-259.

[7]李眉眉.电力负荷混沌特性分析及其预测研究 [D].成都:四川大学,2004:30-40.