西安市降水变化趋势及R/S分析
2011-03-19黄领梅
文 聘,沈 冰,黄领梅
(西安理工大学 西北水资源与环境生态教育部重点实验室,西安710048)
降水是水文循环的重要环节,降水的变化对一个地区水资源的影响很大,严重时会出现不同程度的自然灾害。因此,对西安市降水趋势的分析与预测,对了解西安市水资源的发展趋势进而合理利用水资源有着重要的意义。本文分别选择滑动平均法、Mann-Kendall秩次相关检验法、小波分析法3种方法对西安市降水趋势进行了分析,滑动平均法是最为简单的方法,但是缺乏显著性检验;Mann-Kendall秩次相关检验法是传统的分析方法,是相对成熟应用最为广泛的方法之一;小波分析方法是比较热门相对较新的方法,直观性更强。通过3种方法的对比分析,了解西安市降水的趋势。在趋势分析的基础上利用R/S分析方法进一步估算趋势的持续性,即降水的未来变化趋势。
1 资料与方法
1.1 资 料
采用中国气象科学数据共享服务网提供的西安市1960~2009年50a长系列逐年、逐月实测降水资料进行分析。
1.2 方 法
1.2.1 滑动平均法
滑动平均法[1]是一种在水文气象领域得到广泛应用的方法。其原理是:序列x1,x2,x3,…,xn的几个前期值和后期值取平均,求出新序列yt,使原序列光滑化,这就是滑动平均法。数学表达式为:

当k=1时为3点滑动平均,k=2时为5点滑动平均,k=3时为7点滑动平均。若xn具有趋势成分,选用适合的k,yt就能把趋势清晰的显示出来。
1.2.2 Mann-Kendall秩次相关检验
在众多趋势性分析的方法中,Mann-Kendall(MK)非参数统计法[2]是世界气象组织推荐并广泛使用的一种方法,该方法更适合于水文气象等非正态分布数据。
首先确定序列中对偶观测值 (i<j,Xi<Xj,i,j为序列的时序)出现的个数s,用下式计算其检验统计量:

式中n为系列长度,取α=5%的显著水平,如果时间序列有明显的趋势,则|M|>Mα/2=1.96,若M值为正,表明具有上升或增加趋势,M值为负,则意味着下降或者减少趋势。
1.2.3 小波分析
小波分析[3](Wavelet Analysis)是应用极为广泛的一种数学方法,是在Fourier分析基础上发展起来的时频局部化分析方法。因为小波分析具有强大的多尺度分辨功能,因此能识别出水文序列各种高低不同的频率成分。不同尺度下的低频成分表示水文序列在该尺度下的变化趋势,随着尺度的增加,时间分辨率降低,含有的高频成分信息会随之减少,序列的发展趋势就会表现得更明显。趋势可以看作是周期长度比实测序列长得多的周期成分,通过小波变化获得水文序列的低频系数,再由低频系数的变化过程识别出该尺度下的趋势变化。对于降水序列,只要进行有限尺度的多分辨分析,剩余低频系数可以比较明显地反映降水序列的趋势又不失代表性。本文选用Db3[4]小波函数,利用Mallat算法对降水序列进行分解重构[5],得到不同尺度下的低频序列,进而进行分析,判断序列趋势。
1.2.4 R/S分析
R/S分析方法[1、6],是应用Hurst指数H来判断趋势性成分的强度,反映序列的持续性的一种方法。降水序列的持续性反映降水时间序列前后数据之间的相互关联程度。目前,R/S分析法已被大量应用于水文研究中。
R/S分析方法的基本原理:对于一个时间序列 {ξ(t)}(t=1,2,…),对于任意正整数τ≥1,定义均值序列:

累积离差:

极差:

标准差:

对于比值R(τ)/S(τ)≡R/S,如果存在如下关系:

则说明时间序列 {ξ(t)}(t=1,2,…)存在Hurst现象,H称为Hurst指数,H值可根据计算出的 (τ,R/S)的值,在双对数坐标系 (ln(τ),ln(R/S))中用最小二乘法拟合,H对应于拟合直线的斜率。
根据H的大小可以判断时间序列趋势成分是表现为持续性,还是反持续性。Hurst等人证明,如果 {ξ(t)}是相互独立、方差有限的随机序列,则有H=0.5,将来的发展趋势与现有趋势没有关系;若0<H<0.5时,表明时间序列具有反持续性,将来的总体趋势与现有趋势相反,H 值越接近于0,反持续性越强;而0.5<H<1时,表明时间序列具有持续性,将来的总体趋势与现有趋势保持一致,H越接近1,持续性越强。
2 结果与分析
2.1 滑动平均法
本文采用5点滑动平均,对西安市的年降水及四季降水进行了分析。
图1为年平均降水与5a滑动平均曲线图。由图1可见,西安市的年平均降水在1962~1978年呈略微下降趋势;1979~1982年呈上升趋势;1983~1995年有减少趋势;随后又有略微的上升趋势。

图1 年降水与5a滑动平均曲线Fig.1 Curve of annual and 5a running mean precipitation
图2为春季降水与5a滑动平均曲线图。由图2可见,春季降水1962~1984年变化趋势相对稳定,有略微的下降趋势,1985~1989年有上升趋势,随后又有下降趋势。
图3为夏季降水与5a滑动平均曲线图。由图3可见,夏季降水变化相对稳定并没有明显的趋势,总体呈现略微的上升趋势。
图4为秋季降水与5a滑动平均曲线。由图4可见,1962~1978年秋季降水变化相对稳定,有不明显的下降趋势;1979~1983年呈上升趋势;1984~1989年有下降趋势;随后变化不稳定,呈现上升趋势。
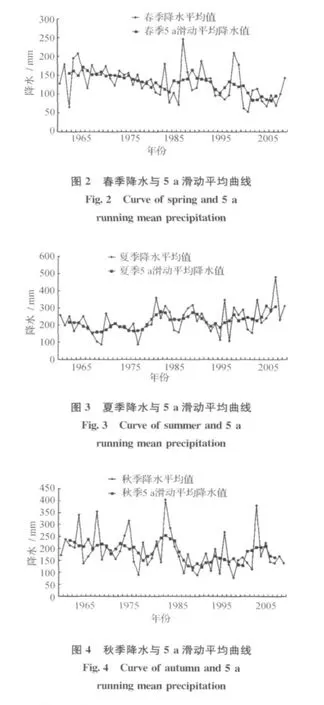
图5为冬季降水与5a滑动平均曲线。由图5可见,1962~1985年冬季降水相对稳定,1962~1974年呈略微上升趋势,1975~1985年有略微下降趋势;随后有明显的上升、下降交替出现的趋势。

图5 冬季降水与5a滑动平均曲线Fig.5 Curve of winter and 5a running mean precipitation
2.2 Mann-Kendall秩次相关检验
根据公式进行计算,结果见表1,取显著水平α=5%,Mα/2=1.96,进行判断。可见,西安市的年降水和冬季降水变化趋势不明显;春季、夏季和秋季降水呈明显的变化趋势,春季和秋季降水呈下降趋势,夏季降水有明显的上升趋势。降水趋势检验结果见表1。
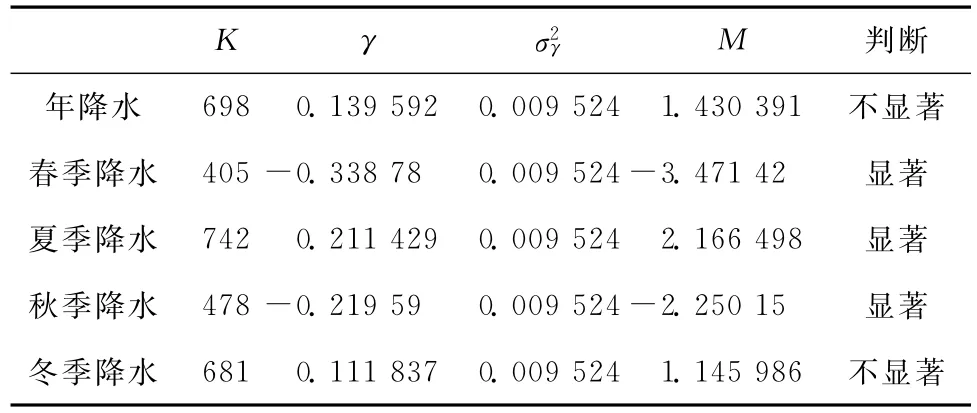
表1 降水趋势检验结果表Table 1 Results of trend test on precipitation
2.3 小波分析
选用Db3小波函数,对西安市50a(1960~2009年)及四季降水进行7层分解并重构,获得不同尺度下的低频序列,进而进行趋势分析。
图6为年平均降水小波分解各层信号图,由图6可见,分解到第5层后,降水呈现上升、下降、上升3个阶段,与滑动平均结果较为相似;到第6层后降水呈现下降、上升两个阶段,变化趋势并不明显;到第7层时,降水总体呈现略微的上升趋势。
图7为春季降水小波分析。分解到第6层后,降水呈现下降、上升两个变化阶段,分解到第7层后,整个时段呈明显的下降趋势,这与Mann-Kendall秩次相关检验的结果相一致。
图8为夏季降水小波分析。由第7层重构小波看出,夏季降水呈上升趋势,该结果与前两种方法分析结果相一致。
图9为秋季降水小波分析。由第7层重构小波可以看出,秋季降水整个时段呈下降趋势,与Mann-Kendall秩次相关检验的结果相一致。
图10为冬季降水小波分析,由第6层看出降水变化相对稳定,由第7层看出冬季降水整体有上升趋势。

2.4 R/S分析
图11~图15是西安市年及四季降水序列的R/S分析,由图11和图15可见,年降水序列及冬季降水序列H值分别为0.541 7和0.495 1,H值接近于0.5,说明西安市50a以来年及冬季降水量变化趋势并不明显,目前的趋势在未来可能发生改变或者趋向于稳定。由图12~图14可见,春、夏、秋季降水序列H值分别为0.711 8、0.777 7和0.751 6,有明显的Hurst现象,H值均>0.5,说明春、夏、秋季降水未来的变化趋势与现有趋势相一致,上升的依然上升,下降的依然下降。



3 结 语
本文利用滑动平均法、Mann-Kendall秩次相关检验法及小波分析的方法对比分析西安市降水趋势,3种方法结果基本一致。滑动平均法最为简便,图中可以直观看出序列变化趋势,但很难反映整体趋势;Mann-Kendall法能定性给出降水变化趋势,并对结果进行显著性检验,是目前利用最为广泛的趋势性分析方法;而小波分析则可以作局部分析,可逐步反映出序列的变化趋势,在趋势不显著时依然可通过逐步分解,获得序列趋势。而R/S分析方法则是对降水未来趋势的预测。
由分析可知,西安市年及冬季降水变化趋势并不明显,有略微的上升趋势;春、秋季降水有明显的下降趋势,并且这种趋势将会持续;夏季降水有明显的上升趋势,同样在未来依然会保留这种趋势。
[1]徐建华.现代地理学中的数学方法:第二版 [M].北京:高等教育出版社,2006:60-61,414-417.
[2]王文圣,丁 晶,金菊良.随机水文学:第二版[M].北京:中国水利水电出版社,2008:34-35.
[3]王文圣,丁 晶,李跃清.水文小波分析 [M].北京:化学工业出版社,2005.
[4]飞思科技产品研发中心.MATLAB 6.5辅助小波分析与应用[M].北京:电子工业出版社,2003.
[5]薛小杰,蒋晓辉,黄 强,等.小波分析在水文序列趋势分析中的应用[J].应用科学学报,2002,20(4):426-428.
[6]张晓伟,沈 冰,孟彩侠.和田绿洲水文气象要素分析特征与R/S分析[J].中国农业气象,2008,29(1):12-15.
