基于核光谱角余弦的高光谱图像FLS-SVM分类算法
2011-03-19赵春晖赵艮平
赵春晖,赵艮平
(哈尔滨工程大学 信息与通信工程学院,哈尔滨150001)
0 引 言
随着光学遥感技术的发展,高光谱遥感无论在军用或民用的各个领域中都发挥着越来越重要的作用。高光谱图像分类是遥感图像处理定量化和智能化发展的主要方面,目前比较成熟的分类方法是基于光谱统计分析的方法,包括监督分类和非监督分类。近几年出现了一些遥感图像分类的新方法,如基于神经网络的分类、基于小波分析的分类、基于分形技术的分类、模糊聚类、树分类器等,但是分类过程仍然存在着如过学习、有限样本、维数灾难等问题。在统计学习理论上发展而来的支持向量机(SVM)[1]是一种能有效解决非线性、过学习、局部极值、维数灾难等一系列难题的监督分类算法,因而在高光谱图像分类中被广泛研究与应用。LSSVM算法提出了用等式约束求解线性方程组,有效地改善了标准支持向量机中不等式约束下求解二次规划的复杂计算过程,同样也能取得良好的分类效果。但无论是标准SVM还是LS-SVM都不可避免地受到噪声或是孤立点样本对分类性能的影响。
引入模糊理论能够有效改善这一缺点,应运而生的模糊支持向量机最关键的问题是模糊隶属度函数的确定[2]。本文引进核光谱角余弦作为一种高光谱图像地物的相似性测度,以一种简单的方式利用这一测度实现对模糊隶属度函数的构造,继而在LS-SVM基础上实现了FLS-SVM算法。实验仿真结果表明FLS-SVM可有效改善LS-SVM的分类性能。
1 模糊最小二乘支持向量机算法
1.1 LS-SVM模型
设给定的训练样本集S= {(x1,y1),…,(xl,yl)}∈Rn,i=1,2,…,l,yi∈[-1,1]。在非线性情况下通过引入变换φ,将样本从输入空间映射到一个高维特征空间。标准SVM二分类问题最终可归结为求解下面的二次规划:

其中ξi为松弛变量;C为惩罚因子。
将标准SVM中二次规划约束条件变为等式,且损失函数变为二次函数,即为最小二乘支持向量机的数学描述形式。引入Lagrange算子αi,得到如下方程:

根据Mercer条件,存在映射φ和核函数K(·,·),使得K (xi,xj)=φ(xi)φ(xj)。令L对变量w,b,ξi,αi的偏导数等于零,并将得到的等式代入式 (2),可得下列矩阵方程:
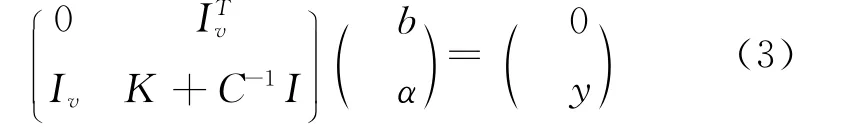
其中y=[y1,…,yl],Iv=[1,…,1];α=[αi,…,αl];K的中元素为Kij=K (xi,xj).i,j=1,2,…,l。
求解矩阵方程(3),最后得到最小二乘支持向量机的函数估计为:
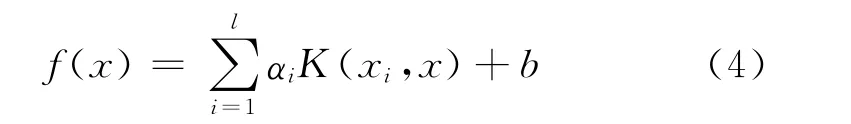
以上便是LS-SVM的数学求解描述模型。
1.2 FLS-SVM模型
为了解决SVM(包括LS-SVM)对噪声及孤立点样本同等对待而使分类性能降低的问题,Lin等将模糊隶属度的概念引入SVM,模糊化输入样本集,提出了模糊支持向量机 (FSVM)的概念[3]。同样把这种模糊理念运用到LS-SVM中,为每一个输入样本赋予一个模糊隶属度,则模糊化训练样本集为S={(x1,y1,u1),…,(xl,yl,ul)},那么模糊化后的LS-SVM求解变换方程由式(3)变为:

式(5)即为FLS-SVM的求解模型,也就是本文采用的算法形式。
2 模糊隶属度函数
对于FSVM,或者是FLS-SVM,关键部分是模糊隶属度函数的构造。不同的隶属度函数会对算法的处理结果以及算法实现的难易程度产生不同的影响。模糊隶属度函数要求能够寻找到一种可以客观、准确地表征系统中样本存在的不确定性测度,而此前提是必须找到一种有效衡量相似性测度的物理量。以往的方法中常常利用距离这种相似性测度来对样本与样本或是样本与类中心的差异性度量,从而设计不同的处理过程从不同角度构造实现这种模糊性反映的函数式,即构造出模糊隶属度矩阵。由于高光谱数据多谱段的特性,即地物光谱信息用光谱向量来表示,如果总光照增加或减少这个向量的长度会随之相应变化但是角度方向保持不变[4]。在多维光谱空间里,不同地物的光谱角度是不同的,那么角度会是一种很好的衡量光谱向量相似性或者说差异性的测度。光谱角度间的差异大小可以理解为其互相归属程度的大小,也是一种不确定性的表述。本文引入核光谱角余弦从向量方向的角度来表征样本间相似性大小的不确定性,并以这一物理量来实现隶属度函数的构造。
1)从数学的角度考虑有其客观性,因为光谱角余弦的范围是0~1,这符合隶属度的数值范围要求。
2)上面分析的引入原因,也说明对光谱向量而言,光谱角余弦是一种相对于欧氏距离表征的亮度差异更为准确的差异性测度。以上两点也是对上文中提到的引入模糊技术改善分类性能的前提要求,做出的一个很好解释。
3)本文提出的新的隶属度函数构造过程极其简单明了,它是相对于其他文献中的方法在效率上更为可选的一种做法,而且也改善了分类效果。
2.1 核光谱角余弦表示
在支持向量机理论应用中,如前文所述我们把原始输入空间通过一种非线性映射φ,将x映射到特征空间里的φ (x),所有的分类过程在特征空间实现。而且因为核函数的特点,可以不必弄清这种非线性映射的具体形式,我们可以利用:

只要知道K (·,·)的具体表达式就能回避φ(x)的求解,实际上只需简单进行输入空间里样本点积运算。在特征空间里基于核的光谱向量角余弦表达式为:
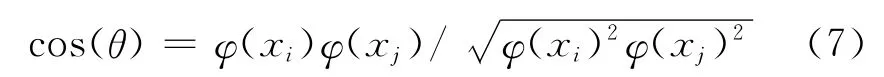
将式 (6)带入式 (7)则得到基于核的光谱角余弦表达式为:
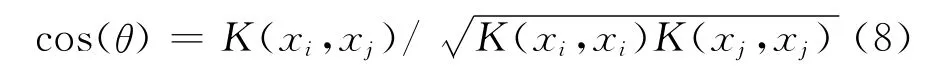
本文选用经典的、常用的高斯径向基核函数:

不光考虑到其良好的非线性映射性能,而且因为因子 (xi-xj)的存在形式,该核函数也是欧式距离的一种表示,体现了样本在特征空间里光谱亮度差异,其次再与角余弦所实现的光谱向量方向表示相结合,很好地融合这两方面的优点来提高分类精度。将式 (9)带入式 (8)得到高斯核下化简后的光谱角余弦:

2.2 光谱余弦值构造隶属度函数的过程
根据余弦角在主值区间上的单调递减特性,余弦值越小 (大)夹角越大 (小),对于光谱向量间则说明二者越不相似 (越相似)。在现有的光谱向量之中,如果能找到最小和最大的光谱向量余弦值,当新的光谱向量输入时只要求其与已知类别的光谱向量角余弦,当其超过最小、最大两范围界限时,可以明确赋予其0表示不属于、1表示属于,而位于之间的数值就是一种模糊不确定性的隶属度值。
基于以上分析,首先计算各样本间的光谱角余弦值,实际上计算K (xi,xj)即可。然后需要找出每一类地物中各训练样本间最大和最小的余弦值,二分类中则找出4个值,2个大值max1,max2,2个小值min1,min2。在2个大值里找出较小的设为zmax,在2个小值里找出较大的设为zmin,这样做是为了放宽对相似性的要求。若是余弦值>zmax则认为两光谱向量方向差异很小判别为一类,隶属度为1;若反之,余弦值<zmin,则认为两光谱向量方向差异很大判别为不同类,隶属度为0;除此之外,余弦值介于zmin和zmax之间的则隶属度为与该余弦值相关的一个数值表示。鉴于以上的分析,要寻找一个函数表达式u=f(cosθ)能让隶属度与角余弦一一对应,这样的函数表达式理论上应该满足以下条件:①定义域为(0~1)时,值域对应为 (0~1);②在上述定义域区间单调递增。
严格来说最好满足f(0)=0,f(1)=1,但是由于这个函数是分段的隶属度函数的一部分,所以对于定义域里的0、1两点一般不会出现在这一部分,因此这个条件可不严格满足。
根据以上限制条件可以找出很多符合的函数表达式,其中比较常用的有指数函数、对数函数和一些三角函数等。而且可以在这些函数形式上加以改动,例如,可以引入可调参数来灵活改变函数的非线性性能从而调控分类性能。无论是哪种形式对分类结果都有一定的改善作用,只不过改善程度大小以及灵活性是不同的。综上,可以选用模糊隶属度矩阵为以下3种形式:
隶属度函数Ⅰ:

其中可调参数满足0≤d≤1;
隶属度函数Ⅲ:)

3 实验结果及其分析
3.1 实验图像
本文采用的是AVIRIS高光谱遥感图像。该图像取自1992年6月拍摄的美国印第安纳州西北部印第安遥感试验区的一部分,它包含了农作物和森林植被的混合区,图像数据特点见表1。原始AVIRIS的220波段图像第50、27、17波段作为RGB通道的假彩色图像见图1。实验采用LS-SVM和FLS-SVM算法对该高光谱遥感图像进行分类比较实验。实验中支持向量机均采用高斯型径向基核函数K(xi,xj)=exp(-(xi-xj)2/σ2)。
3.2 LS-SVM与FLS-SVM分类比较
为了验证本文提出的FLS-SVM分类算法的有效性,用LS-SVM和FLS-SVM分类算法对高光谱图像上相同的3类地物 (监督图像里的2,3,10 3类地物)进行分类。

表1 实验图像数据特点Table 1 Characteristic of experimental image

图1 实验图像的假彩色图像Fig.1 Pseudo-color image of experimental image
3.2.1 LS-SVM分类
在最优参数对为(c,σ)=(1 000,0.02)下,分类结果见表2,图2为LS-SVM分类仿真结果,总体精度用正确分类百分比pcc和Kappa系数给出。
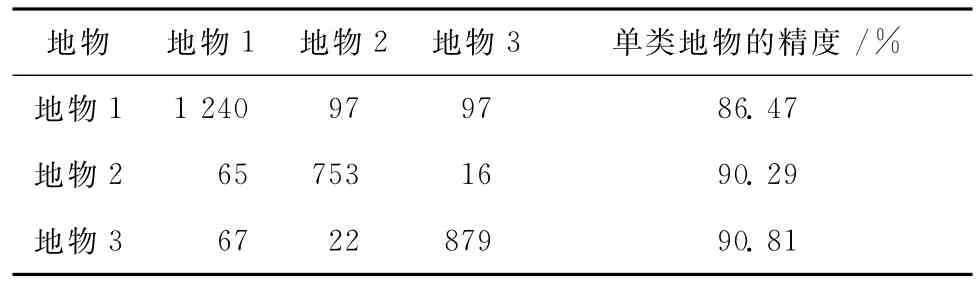
表2 3类地物的分类精度Table 2 Classification accuracy of three objects
总体分类精度:pcc=88.75%,Kappa=82.72%。
3.2.2 FLS-SVM分类
在上述优化参数固定的情形下,利用前文提出的模糊隶属度构造法,下面给出3种不同形式隶属度函数选择下,基于核光谱余弦角的FLS-SVM分类结果的pcc和Kappa值比较,见表3。

由表3可见,采用式Ⅲ作为隶属度函数灵活性更高,此时的混淆矩阵见表4,图3为FLS-SVM分类仿真结果,其中图3(a)、图3(b)分别为真实地物分布和仿真分类图像。

表3 基于核的光谱余弦角的FLS-SVM分类结果Table 3 Classification results of FLS-SVM based on kernel spectral angel cosine /%

表4 FLS-SVM的分类结果Table 4 Classification results of FLS-SVM

表3所示的是利用文中提出的隶属度构造方法实现FLS-SVM算法的结果,最好的效果(表4给出的)与LS-SVM分类结果相比较,分类总体精度有所提高,但程度不是特别大。原因是原始图像的精度不高,AVIRIS图像是从高空拍摄,其分辨率仅为20m×20m,像元混合的概率很大。另外还有一些其它如时令、天气等客观存在的原因,使得分类仍存在一定误差。
4 结 语
对于传统支持向量机分类结果受噪声及孤立点样本影响,而且存在不可分区域的状况,模糊技术逐渐引起人们的重视继而被广泛应用到SVM产生FSVM。而对于模糊理论,最核心的问题是解决模糊隶属度函数的构造。本文主要对隶属度函数做了深入研究,在LS-SVM基础之上,通过引入核光谱角余弦构造隶属度函数实现高光谱图像FLS-SVM分类算法。经实验仿真结果验证,该方法融合了高光谱数据在特征空间光谱亮度和光谱方向角度两方面的信息为一体,提高了LS-SVM的抗噪声能力,改善了分类性能,虽然改善程度不是很高,但是在处理同样的实际问题中,FLS-SVM相对于LS-SVM更适合于未能完全揭示输入样本特性的情况。
[1]Vapnik V.Statistical learning theory[M].New York:Wiley Springer,1998:146-175.
[2]张 英,苏宏业,褚 健.基于模糊最小二乘支持向量机的软测量建模[J].控制与决策,2005,20(6):620-624.
[3]Lin C F,Wang S D.Fuzzy support vector machines[J].IEEE Trans on Neural Networks,2002,13(3):466-471.
[4]赵春晖,乔 蕾.基于改进的最小二乘支持向量机的高光谱遥感图像分类[J].应用科技,2008,35(1):44-47.
[5]张秋余,竭 阳,李 凯.模糊支持向量机中隶属度确定的新方法 [J].兰州理工大学学报,2009,35(4):89-93.
[6]Lei Chen,Geng yang,Ying zhou Zhang,et al.Web services clustering using SOM based on kernel Cosine similarity measure[C]//2ndInternational Conference and Engineering,2010.
[7]Shiqing Zhang.Speech emotion recognition based on fuzzy least squares support vector machines[C]//Proceedings of the 7th World Congress on Intelligent Control and Automation,2008,1 299-1 302.
[8]Xiaowei Yang,Guang quan Zhang,Jie Lu,et al.A kernel fuzzy c-means clustering-based fuzzy support vector machine algorithm for classification problems with outliers or noises[J].IEE Transacations on Fuzzy Ssystems,2011,19(1):105-115.
[9]Liang Xu,Xiao Bo Zhang.Incorporating prior knowledge in a fuzzy least squares support vector machines model[C]//Sixth International Conference on Natural Computation,2010,344-348.
