黑河日径流量混沌变化特性的研究—Ⅲ最大李雅普诺夫(Lyapunov)指数的确定

2011-03-19陈引锋马长铃

地下水 2011年3期

陈引锋,马长铃

(陕西能源职业技术学院,陕西咸阳 712000)

要将混沌分析法应用于水文系统中,首先需要研究水文序列是否为混沌时间序列,即判别水文系统的运动形式是否为混沌运动,进行混沌性识别或序列性质鉴别。水文系统是一个远离平衡态的复杂的开放系统,又是一个动态的非线性系统[1]。一方面,它是由许多因素相互作用相互影响而演化形成的一个整体,另一方面,它又受到外界自然力的作用及不同程度的人类活动的影响,从而形成了水文系统复杂的演化规律。因而水文系统中表现出混沌特征是可能的,且有关文献研究已经予以证明[2][3]。

1 水文系统混沌特性的识别

在实际的水文数据序列中,噪声与混沌往往并存,既有确定性成分,也有随机性成分。对于观测资料有噪声且长度有限的水文资料序列,进行混沌性的识别,基于目前的混沌理论水平,大都是从某一个方面判别水文序列是否满足混沌序列的某些必要条件[4],只能得出可能具有混沌特征的结论,而不能给出水文序列具有混沌特征的肯定答复,因此需要采用尽可能多的方法来鉴别水文序列,水文时间序列的鉴别,可以从定性、定量以及将两者结合起来的途径进行,方法众中,具体包括有李雅普诺夫(Lyapunov)指数、测度熵、分维数、自相关函数、标度指数、功率谱指数及关联维数法等[5][6]。

利用这些方法进行时间序列混沌性质的判别,实际上需要利用时间序列,重构相空间,计算混沌量水平,也就是吸引子的不变量。混沌理论认为,决定系统长期演化的任一变量的时间演化,均包含了系统所有变量长期演化的信息。因此,通过决定系统长期演化的任一单量构成的时间序列可以研究系统的混沌行为。大多数水文问题都是由许多变量组成的动力系统,选用系统的单个或多个重要变量构成单维或者多维时间序列,进行水文系统的重构,在相空间中刻划 N维水文系统的混沌吸引子,从而揭示出传统坐标系无法揭示的水文现象演化规律。吸引子的不变量(吸引子分维数、Lyapunov指数、测度熵等)表征了系统的混沌性质,是混沌系统的重要特征量[7]。

在《黑河日流量混沌特性的研究—Ⅰ》中[8],通过观察自相关函数的图像发现,自相关函数随嵌入滞时迅速衰减,且带有一个指数尾巴,表明该系统是混沌运动。在《黑河日流量混沌特性的研究—Ⅱ》中指出[9],吸引子分维数为 2.1,可以认为,该动力系统具有混沌特征,本论文就是在此基础上,通过确定最大李雅普诺夫(Lyapunov)指数的值,进一步论证黑河日流量时间序列的混沌特性。

2 最大李雅谱诺夫(Lyapunov)指数

Lyapunov指数用于量化初始相近的轨道的指数发散和估计系统的混沌量,从整体上反映了动力系统的混沌量水平,表征了系统的混沌性质。混沌运动的基本特点是运动对于初始条件极为敏感。两个靠的很近的轨道线,随时间的推移按指数方式分离。Lyapunov指数就是从整体上定量描述轨道的平均分离或者收缩的快慢。n维的动力系统具有 n个Lyapunov指数,代表了 n个方向系统的轨道之间的分离程度。在 Lyapunov指数小于零的方向,轨道收缩,运动稳定,对初始条件不敏感;在Lyapunov指数大于零的方向,轨道分离,对初始条件敏感。所有 Lyapunov指数的和大体上表征了轨道总的平均发散快慢,而最大的 Lyapunov指数决定了轨道发散,覆盖到整个吸引子的快慢。因此最大 Lyapunov指数为正,常常被作为判断混沌性质的重要条件,而最大 Lyapunov指数的倒数可以作为最大可预测长度的估计值[10]。

目前,计算 Lyapunov指数的方法很多,包括定义法、Wolf法、Jacobian法、P-范数法、Rosentstein小数据量法等等。其中 Wolf法对于噪声和数据量要求较高,适用于无噪声序列,切空间中小变量的演变高度非线性,只能较可靠地估计最大Lyapunov指数[11];Jacobian法可用于有噪声的序列,切空间中小变量的演变接近线性。两者对轨道分布不均匀的情况计算效果较差。而范数法避免了两者的共同弱点[10],但是计算量大,Rosentstein小数据量法,具有计算量小,对小数据序列可靠,可用于有噪声的情况等优点。因此,本文选用Rosenstein小数据量法计算最大 Lyapunov指数。

2.1 计算原理与方法

我们认为选择让相空间重构的紧邻的两个点跨越整个轨道周期是合理的且是非常必要的,我们姑且称这两个点为“紧邻点对”。最大 Lyapunov指数是大量紧邻点对在轨道方向上指数发散率的平均[12]。

在大多数实际的耗散系统中,状态变量不能趋于无穷,对非线性系统在给定状态附近线性化,在局部得到类似最简单的线性常微分方程

它的解可以写为

如果 a＞0,则在初始时刻相邻的两条轨道,在下一时刻要按指数速率分离开。a＜0时,它们之间的距离按指数消失。a=0时,不同初值给出不同的平行线,它们之间的距离永不改变。一般说来,x是矢量,而 a是依赖于给定的线性化点的矩阵。这个矩阵的特征值决定相邻两点间的拉伸、压缩或转动,其速率可能在相空间中各点不同。对运动轨道各点的拉伸或压缩速率进行长时间平均,就是刻划这种整体效果的 Lyapunov指数。

定义[12]:对于一维动力系统,xn+1=F(xn),初始两点迭代后的分离与靠拢情况取决于导数︱dF/dx︳的值。若︱dF/dx︳＞1,则迭代使两个初始点分离;若︱dF/dx︳＜1,则迭代使两个初始点靠拢。在不断迭代过程中,︱dF/dx︳的值也不断改变。此改变量对迭代次数(即时间)取平均,从整体上看两相邻状态的分离情况。每次迭代后所引起的指数分离中的指数为 ,则原来相距为的两点经过n次迭代后相距为:

取极限得:

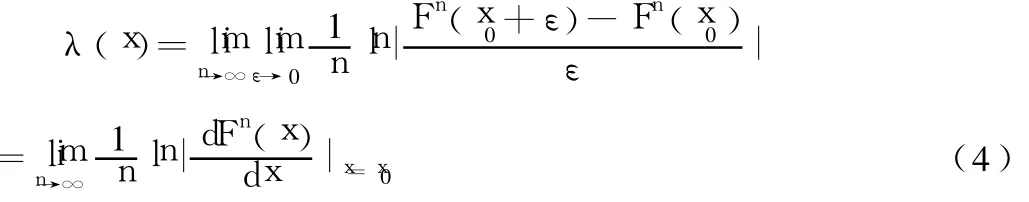
通过变形简化为:

λ称为原动力系统的Lyapunov指数。

对于一般的 n维动力系统,定义Lyapunov指数如下:设F是 Rn→Rn上的n维映射,决定一个维离散动力系统 Xn+1=F(Xn)。设系统的初始条件用一个无穷小的 n维的球表示,随着时间的演变过程变为椭球。将 n维椭球的 n个主轴按其长度顺序排列,λ1≥λ2≥λ3≥…≥λn,那么第 i个 Lyapunov指数根据第 i个主轴的长度 Pi(n)的增加速率定义为

n个Lyapunov指数表示了系统在相空间的n维方向的收缩或者扩张的性质。椭球的主轴长度按 ei增加,前 i个Lyapunov指数的和表示了前 i个主轴定义的 i维立体体积按指数增加的长期平均速率。最大的 Lyapunov指数决定了轨道发散覆盖整个吸引子的快慢,最小的 Lyapunov指数决定了轨道收缩的快慢,而所有 Lyapunov指数大体上表征了轨道总的平均发散快慢[12][13]。

2.2 计算过程

Lyapunov指数的计算需要基于相空间重构[12][13]。对于数据长度为 n的单变量时间序列 x1,x2,…,xn,在嵌入维数为 m,时间延迟为 τ的重构相空间内,相点 yi=(xi,xi-τ,xi-2τ,…,xi-(m-1)),选取所有的 N=n-(m-1)τ个相点为参考点,以参考相点 yi及其在相空间内的最邻近相点 yir,作为相邻轨道的起始点,来考察相邻轨道的指数分离情况。在时间下标为 i的时刻,轨道的距离为初始距离(采用欧几里德距离)。

由于混沌系统的轨道分离具有指数分离特点,则

最大 Lyapunov指数可表示为

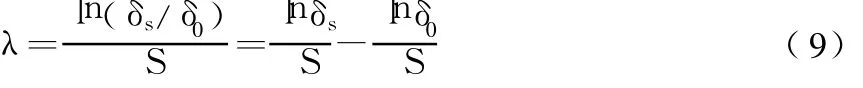
如果对 N个相点及其邻近点经过 s步演化后的分离距离取整体平均值

然后取其自然对数,绘出的曲线图,选取曲线图中的线性部分进行直线拟合,所得的斜率是全局最大 Lyapunov指数。

2.3 结果与分析

根据式(8)和式(10),采用 Matlab软件计算最大 Lyapunov指数。

由《黑河日流量混沌变化特性的研究—Ⅰ》与《黑河日流量混沌特性的研究—Ⅱ》一文可知,时间延迟 τ=10,嵌入相空间维数m=9。为了考察计算方法对于嵌入维数和时间延迟的依赖性[14],分别对 τ=10,m=8,9,…,13和 m=9,τ=7,8,…,15的情况进行计算,计算结果 lnδS～S曲线见图 1和图 2所示。

图1 R法计算最大 Lyapunov指数(τ=10)

由图 1可以看出,当 m逐渐增大时,每个 m值的曲线上都出现了多个波峰跳跃,但是其跳跃阶段的顶点明显位于同一直线上,具有线性规律。对于 m=10,11,12,13时曲线的波峰包络线,作直线拟和,斜率明显是大于零的,并随着 m的增大,斜率在减少。根据前述计算结果,取 m=9,τ=10,对应图中第三条曲线,为了进一步计算方便期间,将图 2的局部部分进行放大如图 3所示。