交互式偏好满意优化在渔船技术经济论证中的应用

陶冶,吕显强,杨文莲,贾复

(大连海洋大学信息工程学院,辽宁大连116023)

交互式偏好满意优化在渔船技术经济论证中的应用

陶冶,吕显强,杨文莲,贾复

(大连海洋大学信息工程学院,辽宁大连116023)

针对在玻璃钢渔船技术经济论证中多目标优化的权重设计问题,提出一种交互式偏好权重的遗传算法,使决策者能够在多衡准满意优化中的当前群体中,将对于个体的偏好转换为对于权重数值的偏好关系,利用它们重新构造适应度函数,并作为在Pareto遗传算法的偏好优化方向。通过多次的进化后,决策者能够获取最满意的优化解。该方法避免了传统多目标船型论证中需要事先确定优化目标的权重且才能进行综合评判的缺陷,经玻璃钢渔船经济技术论证的计算实例论证,该方法是可行且有效的。

Lp范数;遗传算法;权重优化;交互式

船型论证的目的就是优化船型方案。在众多的船型方案中,要把最优的船型方案找出来需涉及两个问题:一是评价指标,即船型要素优化的标准;二是寻优方法。所谓渔船的技术经济评价指标,就是代表渔船船型要素优化的目标函数或综合评判的评价标准集,可以是单目标或是多目标评价指标体系;而寻优方法也是多种多样的。根据中国目前的实际情况,渔船技术经济评价指标的选择或确定如下:1)净现值(NPV),这是目前国际通用的经济性评价指标,以高为好;2)油耗吨鱼,选择该指标是因为柴油在国内是一项重要资材,其成本占渔船总成本的1/4～1/3,以低为好;3)年产量,考虑最大限度满足市场的需求,以大为好。

对船型论证的过程实际上是在渔船、渔场、渔港和渔业市场所组成的系统中寻优。衡量一个方案优劣的评价标准通常不止一个,往往会涉及到多个目标函数的优化。通常这些目标函数是不可比较的,甚至是互相冲突的,很难获得使每个目标都能够达到最优的优化解。采用满意度方法的优点在于可以将目标函数转化为决策者的满意程度。

在船型多指标决策问题中,首先必须确定各指标的权重。指标权重的确定有主观法和客观法两大类。权重系数代表对目标满意度的偏好程度,然而选择准确并且合适的权重系数通常是很困难的,主要依赖于决策者所具备的经验和知识水平。常用的基于权重的主要优化方法有:1)定权重法。该方法在综合评判中采用固定权重数值,其主要缺点是决策者必须预先设定合适的权重系数值[1]。2)随机权重法。该方法由Murata等[2]提出并应用到遗传算法中。在该方法中,由于使用随机分配权重系数,使每个个体具有相等的选中机会进化到Pareto边界。此外,Zheng等[3]提出了另外一种随机权重方法,桑松等[4]提出了熵权系数法。上述几种方法在遗传算法应用中很难反映决策者对每一进化代中权重的偏好信息。在许多情况下,决策者在优化开始之前很难决定最合适的权重系数,可能需要比较和分析一代或者若干进化代后的群体特点,交互式地修改目标权重系数,以确保遗传算法能够沿着决策者最满意的方向进化。

本研究中作者提出了一种交互式的满意遗传算法,在遗传算法中采用多点进化分类模型,完善并构造了样品点完整的二元关系[5],并利用它构建了非线性优化的可行域,通过优化最满意点和最不满意样品点Lp的范数,以获取优化目标的偏好权重和交互式重新构造遗传算法的适应度函数,使决策者能够利用该权重来引导遗传算法进化到决策者偏好的方向,以获取最满意的优化解。

1 满意优化

1.1 满意度原理

“令人满意准则”是由诺贝尔奖获得者Simon提出的。他认为在某些情况下,应当用“令人满意解”来代替传统意义的最优解[6]。“令人满意准则”为人们解决实际问题开辟了一条新途径。目前,对满意度原理的研究可分为两大类:一是以Takatsu[7]为代表,主要研究满意度的数学基础和数学特征;二是以Goodrich等[8]为代表,主要研究满意度理论的应用。满意度原理在满意控制、满意决策及分配、满意解的神经计算等方面都有广泛的应用。

1.2 多衡准满意优化[9]

已知决策向量定义如下:

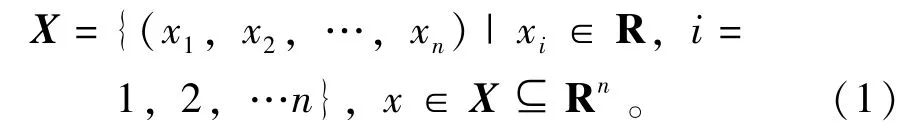
而质量集合Q表示为

其中qk=fk(x),k=1,2,…,m。给定满意映射函数hk:R→[0,1],sk=hk(qk),k=1,2,…,m,满意度函数向量可以表示如下:

在设计实践中,综合满意度函数fop:[0,1]m→[0,1]根据问题的特性可以定义为不同的表达形式。采用线形权重和综合满意度函数的表示如下:

因此,多衡准的满意优化问题可以转化为如下不等式约束的优化模型:

本研究中以式(5)作为满意遗传算法的综合满意度函数及权重来进行优化设计。

2 基于权重优化的交互式偏好满意遗传算法

2.1 个体的二元关系

在遗传算法的群体中,由于决策者对于每个个体具有不同的重视程度,导致两个个体具有不同的偏好关系。为了评价个体之间的关系,本研究中使用表1中所列符号来表示任意两个样品个体之间的二元关系。

表1 二元关系及符号表示Tab.1 Binary relations and symbols

在表1中,d表示两个样品个体综合满意度的差异。假设选定样品点集为xk,xk-1,xk,xk-1∈X,则dk可表示为下式:

其中:dk表示两个样品个体偏好程度的差异,如果dk为正数,表示xk要优于xk-1;如果dk为负数,表示xk劣于xk-1;如果dk近似为零,表示xk与xk-1为等价关系。考虑到问题的对称关系,本研究中重点考虑dk＞0的情况。

在表1中第3列给出了5种二元关系相关的域值条件,该条件可以作为两个样品个体偏好程度的规则。表中ε为一个非常小的正数(可取为10-5),可以作为二元相等符号关系≈的边界值;此外,α,β(0＜ε＜α＜β＜1)也分别代表符号关系偏好≻、非常偏好≻≻的上限值。它们可以看作不同样品个体偏好程度的度量。

2.2 偏好可行域下的权重Lp范数优化

根据前述权重优化原理,遗传算法需要获得合适的权重数值来引导群体朝着决策者偏好方向进化。因此,有必要将一些样品个体的偏好关系转化为综合满意度函数的权重偏好信息。为了能实现该要求,本研究中采用如下优化方法:

定义L为决策者选择样品的个体集合,l为该集合的长度,如下式所示:

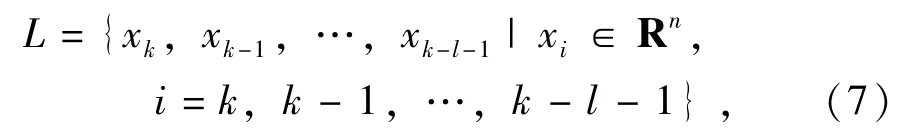
其中,假设样品集L中各个个体的偏好关系如下:

如果以式(8)构造偏好可行域,使用xk,xk-l-1满意度的权重Lp范数作为目标,非线形偏好可行域下的权重优化模型表示如下:

式(9)的实际含义为:在满足决策者对于样品集中所有个体偏好程度的约束前提下,寻求能够使最不满意个体与最满意个体的Lp范数达到最小的权重。该式的应用主要达到两个目的:一是可以保证优化后的权重能够体现决策者的实际偏好,二是由于权重优化后样本个体的满意度差异趋于最小,在一定程度上能够提高遗传算法的收敛速度。

3 遗传算法搜索

为了能够使用遗传算法搜索到Pareto最优的解,对于多满意衡准的满意优化问题,有必要首先找到完整的Pareto解集并把它们尽可能分布到Pareto边界上,以便决策者能够在该边界上进行权衡。Goldberg[10]提出了Pareto遗传算法,该方法采用了基于Pareto解的分级方法和适应度分配方法,可以有效地保证在群体中获取相应的非支配个体。本研究中提出的方法综合了Pareto遗传算法和偏好权重(方向)法,对于决策者更具有吸引力。首先,通过Pareto遗传算法,Pareto优化解集可以很容易的获得;其次,使用权重优化的个体趋向于朝向偏好的进化方向移动(图1)。当优化过程结束后,决策者可以获取满意的Pareto偏好解。

图1 决策者偏好的移动方向Fig.1 The direction of movement determined by DM

4 应用实例

为了研究交互式偏好满意优化在渔船技术经济论证中的效果,本研究中采用近海小型玻璃钢拖网渔船船型的满意优化为算例,其优化的数学模型如下:

系统设计变量取X=[x1,x2,x3,x4,x5,x6]T= [Lbp,B,D,T,BHP,d],主要船体性能约束条件如下:25 m≤Lbp≤35 m,5 m≤B≤7 m,2.6 m≤D≤3.2 m,2.0 m≤T≤2.5 m,150 kW≤BHP≤325 kW, 10 d≤d≤20 d,9.5 kn≤vs≤11.5 kn,D-T≥Fmin, GM≥GM0。

此外,考虑到模糊因素的影响,受模糊影响的部分约束条件如下:

(2.9-B/T)/0.2≥λ, (0.50-CB)/0.01≥λ,

(VF-100)/50≥λ, (d-10)/2≥λ,

((D-T)-0.6)/0.3≥λ。

上述约束中左边分母值为约束容差,λ为模糊截集水平,可以通过模糊综合评判来确定。

为了简便和说明问题的需要,本算例中的渔船技术经济评价指标采用双目标,分别为净现值NPV、吨鱼油耗,如下式所示:

两个目标函数涉及的相关经济性计算公式如下:

式中:qi(i=1,2)为单船平均网次产量;ki(i=1,2)为连青石渔场(大沙渔场)资源情况系数; VFi(i=1,2)为两个渔场的渔舱容积(i=1为连青石渔场,i=2为大沙渔场);VF为渔舱容积;ni(i=1,2)为作业天的投网次数;di(i=1,2)为作业天数;Sf为渔获物的积载因数;LBD为立方数;DW为排水量;CL为空船质量系数;pp为工况系数,出港时pp=1.0,满载离开渔场时pp= 0.3;O为燃油及润滑油质量;W为淡水质量;F为食品质量;M为全体船员及行李质量;Wn为网具总质量;Wb为备品质量;WC为煤质量;Wi为冰质量;GM为单个船员及行李质量;Ms为船员人数;Lbp为玻璃钢拖网渔船垂线间长;vs为服务航速;BHP为主机功率;dSi(i=1,2)为渔港至渔场航行天数;Si(i=1,2)为渔港至渔场距离;k3为安全系数;k4为主机每千瓦小时的耗油量;Mi(i=1,2)为全年往返渔场次数;QO1为主机耗油量;QO2为辅机耗油量;QO为总耗油量;g1为润滑油每千瓦小时的耗油量,取0.00294 kg;ABHP为辅机功率;QH为总润滑油耗油量;Qf为年渔获量;P为年利润;Fp为鱼价;Ca为渔捞年费用; Op为油价;OHP为润滑油价;Sa为船员工资;RC为年维修费,玻璃钢渔船维修费按钢质渔船的15%计算;Me为年管理费用;OLd为年折旧费,按钢质渔船的80%计算;IC为保鲜冰费;Ne为网具费用;n为渔船寿命;Iv为初始投资,即拖网渔船造价与网具成本;SI为玻璃钢拖网渔船造价;Hn为网具的成本。

在遗传算法设计中,群体规模为80,交叉概率为0.8,变异概率为0.001,个体的选择采用Kiyota等[11]提出的选择和共享法,其中个体的选择方法采用锦标赛选择法。

假设在最满意船型论证中存在两种类型的偏好方向,决策者选择3个样品个体来计算优化权重数值ω1和ω2,每隔10代重新构造适应度函数sw。经过50代进化后,每个个体的满意度s1和s2在群体中的分布特性如图2所示。

图2 5次偏好优化后群体中满意解的分布情况Fig.2 Distribution of satisfactory solutions after five interactive preferred directions

图2 -a1、b1表示遗传算法初始阶段在群体中个体的分布;图2-a2、b2为经过3次偏好优化后的群体分布图;图2-a3、b3为经过5次偏好优化后的群体分布图。从图2可见,在两种偏好情况下群体均能进化到Pareto边界;此外,从图2-a3和图2-b3中也可以看出,经过5次偏好优化后,能够保证最终群体中个体的移动方向与决策者偏好的方向相一致。当遗传算法进化结束后,决策者能够更加方便和有效地进行权衡决策。

与传统的船型技术经济论证方法不同[1,4],本研究中提出的方法没有采用先进行寻优,然后在最优点附近选择若干可行的方案,并利用模糊综合评判或线性加权评判等定权重的方法进行方案排序和优选,而是充分利用遗传算法的种群优化特性,即在每次优化过程中能提供多个侯选解,决策者可以预先选择一些样品个体以构成样品个体集合,并利用任意两个个体之间的二元关系,构造偏好可行域。通过遗传算法的搜索,决策者可以选择在若干代进化结束后,比较群体中指定样品个体,交互式地修改权重系数和适应度函数的数值,直到获得最满意的优化解,将寻优和方案的选择同步完成,图2两种偏好方向获得的满意船型如表2所示。

表2 两种偏好方向优化结果对应得到的船型参数Tab.2 The optimum result of two preferred directions

从表2的计算结果可见,当偏好方向变化时,可以获得不同的满意优化船型。图2-a反映了决策者偏好吨鱼油耗的情况,因此获得船型的主机功率和航速偏低;而图2-b反映了决策者对于NPV的偏好情况,考虑了鱼价和渔场距离等要素,获得的鱼舱容积和航速较大。由此可见,使用本研究中提出的交互式满意遗传算法能够确保群体进化方向始终与决策者偏好的方向相一致,当遗传算法优化结束后,决策者能够获得满意的船型。

[1] 陈龙.远洋渔船及渔船队的技术经济分析[D].上海:上海交通大学,1996.

[2] Murata T,Ishibuchi H,Tanaka H.Multi-objective genetic algorithm and its application to flow shop scheduling[J].Computers and Industrial Engineering,1996,30(1):957-968.

[3] Zheng D,Gen M,Cheng R.Multiobjective optimization using genetic algorithms[J].Engineering Valuation and Cost Analysis, 1999,2(1):303-310.

[4] 桑松,林焰,纪卓尚.基于交互式多目标决策的船型技术经济评价决策系统[J].中国造船,2002,43(3):1-6.

[5] 王小平,曹立明.遗传算法——理论应用与软件实现[M].西安:西安交通大学出版社,2002.

[6] Simon H A.管理决策新科学[M].北京:中国社会科学出版社, 1998.

[7] Takatsu S.Latent satisfactory decision criterion[J].Information Science,1981,25(3):145-152.

[8] Goodrich M A,Stirling W C,Frost R L.A Satisficing Approach to Intelligent Control of Nonlinear Systems[C]//Proceedings of the IEEE international Symposium on intelligent Control.Dearborn,M I,USA:IEEE,1996,2:15-18.

[9] 陈春俊,罗刚,胡永忠.控制系统设计中的满意优化原理[J].电子科技大学学报,2000,29(2):186-189.

[10] Goldberg D E.Genetic Algorithms in Search:Optimization and Machine Learning[M]//Ma,USA:Addison-Wesley Publishing Co.Inc,1999.

[11] Kiyota T,Tsuji Y,Kondo E.An Interactive Fuzzy Satisfactory Approach Using Genetic Algorithm for Multi-objective Problems [C]//Joint 9th IFSA World Congress and 20th NAFIPS International Conference.Vancouver,BC,Canada:IEEE,2001,2:757-762.

Evaluation of optimum fishing FRP ship types by an interactive preferred satisfactory optimization

TAO Ye,LÜ Xian-qiang,YANG Wen-lian,JIA Fu
(School of Information Engineering,Dalian Ocean University,Dalian 116023,China)

In view of the weight coefficients problem in multiobjective evaluation of optimum FRP fishing ship type, an interactive satisfactory method was proposed for Genetic Algorithm(GA),which can make DM turn the preference for individual into for weight value,and used to reformulate evaluation function as the preferred optimization direction for Pareto GA,and finally DM can acquire the corresponding optimal satisfactory solution.The method avoids presetting the weight in traditional multiobjective ship type evaluation,and an economic and technological evaluation of FRP ship type is used to demonstrate that the proposed method is of availability and efficiency.

Lp-norm;genetic algorithm;weight optimization;interactive

U662.2

A

2095-1388(2011)04-0371-05

2010-04-26

辽宁省教育厅高等学校科研计划项目(2008146);辽宁省优秀青年骨干教师资助计划项目(2006)

陶冶(1974-),男,副教授。E-mail:taoye@dlou.edu.cn