基于双层规划模型的交通信号区域协调控制*

徐建闽 首艳芳 卢凯

(华南理工大学土木与交通学院，广东广州510640)

随着城市化进程的加快，道路交通供需矛盾日趋扩大，所引发的交通堵塞、交通事故和交通环境恶化等现象日益严重.增加基础设施投入、扩建和新建道路等传统手段仍然无法解决问题，单独从道路或车辆方面考虑都难以提高城市路网的通行能力.现代交通研究从信号控制入手，其中如何实现多个交叉口相互协调使整体区域达到最佳通行状态越来越受到研究人员的重视，特别是近年来在协调控制模型建立与协调控制策略选取方面的研究已取得较大进展［1-4］.

目前已有的相关文献中，对交通信号区域协调控制的研究还处于理论阶段.文献［5］中对交通均衡分配模型为基础的双层数学规划模型进行改进，构造了城市交通网络的区域协调控制模型，但未证实模型的有效性;文献［6］中提出基于多智能体的分布式区域协调控制方法，但优化目标函数模糊，不一定能达到最优化;文献［7］中提出一种基于D-S证据理论的实时协调控制方法，存在搜索速度慢和精确度不高等问题;文献［8］中构建了一种分布式Q学习多智能体的交通信号区域协调控制策略，但无法保证学习算法的收敛性;文献［9］中采用两层递阶分布式结构提出一种基于改进免疫遗传算法的城市交通自适应区域协调控制方法，但目标函数比较简单;文献［10］中提出一种基于遗传算法的过饱和交通状态下的区域协调控制模型，然而模型只适用于车辆单向放行的情况.实践证明，TRANSYT (Traffic Network Study Tool)、SCOOT(Split Cycle and Offset Optimization Technique)和SCATS(Sydney Coordinated Adaptive Traffic System)三大典型区域协调控制系统只适用于非拥挤交通状况，在一定程度上限制了区域协调控制系统的实际运行效果.

在交通信号区域协调控制系统中，各交叉口既有自己的效益目标(即确保本交叉口交通畅通)，又必须服从所属子区甚至整个区域的整体效益目标(即提高区域交通的通行能力)，因此区域整体效益与各交叉口之间存在一定的层次关系，采用双层规划模型来描述这种关系是适宜的.尽管有关双层规划理论的应用已经不少［11-12］，但真正应用于交通信号控制的研究成果却寥寥无几.文中针对近饱和或过饱和状态下的交通信号区域协调控制问题，基于遗传－模拟退火算法提出交通信号区域协调控制的双层规划模型及其求解方法，为实现城市交通自适应区域协调控制提供一条新方法.

1 双层规划问题

双层决策是一类具有主从递阶结构的系统优化问题，其上层优化问题的约束域由另一个优化问题(下层问题)决定［13］.该问题的数学模型为

式中:x∈Ra，y∈Rb，W，w:Ra×Rb→R，G:Ra×Rb→Rp，g:Ra×Rb→Rl，a、b、l、p取整数，x为上层决策者的决策变量，y为下层决策变量，W(x，y)、w(x，y)分别为上、下层决策者的目标函数.模型的决策机制是上层决策者首先宣布决策x，这一决策将影响下层决策问题的约束集和目标函数，下层决策者在这一前提下选择使自己的目标函数达到最优的决策y，上层决策者再根据下层决策者的反应做出符合全局利益的决策，直到目标函数达到最优为止.

2 区域协调控制双层规划模型

2.1 模型构建

常态协调控制策略以绿波带宽最大化和延误最小化作为控制效果评价指标，但仅适用于没有形成车辆排队或者车辆排队较短、不会对上游交叉口造成任何影响的情况.当交通量接近或超过道路的设计通行能力时，交叉口形成较长的排队车辆不可避免，此时对于区域协调控制而言，如何将各交叉口的排队车流控制在一定的范围之内以避免交通堵塞、保持系统通行能力最大则更为重要.

定义一个协调控制子区的交叉口数为N，n为任一交叉口，Sn为交叉口集合，n∈Sn;Pf为交叉口相位的集合，f∈Pf;F为最大相位数，F=2，3，4，…; I为交叉口n进口道i的总数;Lout为区域边界输出路段的集合;tfn(k)为第k个信号周期交叉口n第f个相位的有效绿灯时间;qi(k)为第k个信号周期进口道i的车辆平均到达率;ufi(k)为第k个信号周期第f个相位进口道i的滞留车辆数;si为进口道i的饱和流量率;T为交叉口周期时长;Q为交叉口通行能力.

各进口道在信号周期绿灯结束时的滞留车辆数不仅与本信号周期的信号控制参数和车辆到达情况有关，而且受前一个信号周期结束时的滞留车辆数的影响，同时约束下一个信号周期的延误.考虑了车辆到达率的随机波动如图1所示，图中tR为红灯时间，tG为绿灯时间，Ai(k)为车辆到达累积线，Di(k)为车辆驶离累积线，两条线之间的距离就是滞留排队车辆数.在第一个信号周期内，进口道的到达车辆数(qiT)明显小于最大可放行车辆数(QT)，绿灯结束时进口道排队车辆数为0;在第二个信号周期内，到达车辆超过其可通行车辆数，绿灯结束时进口道存在滞留排队车辆，在计算各相位滞留排队车辆数时需要动态考虑各参数的变化.

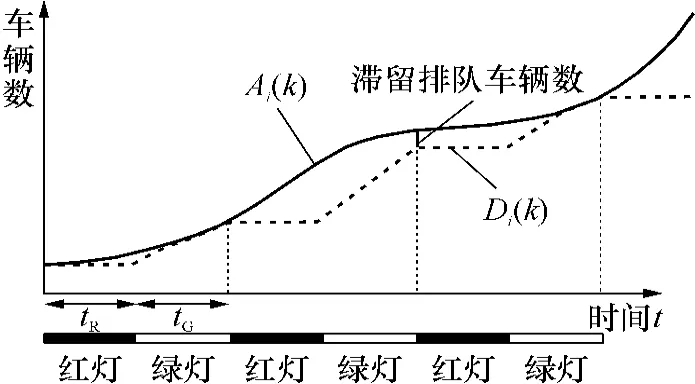
图1 车辆到达率的随机性分析Fig.1 Randomness analysis of vehicle arrival rate

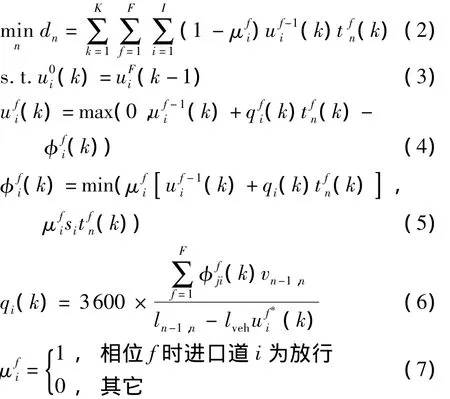
式中:dn为控制时间KT内交叉口n各进口道的延误时间之和，K=1，2，3，…定义相位f时进口道i是否为绿灯状态)为第k个信号周期从进口道i驶出的车辆数;(k)为第k个信号周期从上游进口道j驶出到下游进口道i的车辆数;vn－1，n为车辆从交叉口n－1行驶到交叉口n的平均速度; ln－1，n为交叉口n－1与交叉口n之间的距离;lveh为排队车辆的平均长度;式(3)表示第k个信号周期开始时进口道i的排队车辆数等于第k－1个信号周期最后一个相位结束时的车辆数;式(4)表示第f个相位内，如果从进口道i到交叉口n上的延误排队车辆数(k)与当前相位内实际到达的车辆数之和大于当前相位交叉口能放行的车辆数，则为二者之差，否则为0.式(5)表示第f相位内，如果排队车辆数加上相位内到达的车辆数小于最大可放行车辆数，则，否则为).

2.2 约束条件分析

交通区域协调控制的上层目标是使控制周期内通过区域的总车流量最大，即驶离区域边界输出路段的车辆数最大.定义¯Q为控制时间KT内驶出区域的总车辆数，根据交通流理论建立上层规划模型为

影响区域协调控制效果的主要因素有相邻交叉口间距、路段交通量以及交叉口信号配时参数等.相邻交叉口间距过大，上游交叉口驶出车队会随行驶距离的增长逐渐离散开来，驶近下游交叉口时将呈现随机达到状态，协调控制作用明显减弱;路段交通量过小，交叉口之间剩余较大的存车能力，车流行驶离散性强，控制协调效果不明显;交叉口信号配时参数有效调节路段交通量和决定协调控制实时效果，是决定协调控制策略优劣的另一类主要因素.

2.2.1 相邻相位差

相邻交叉口之间的相位差将直接决定行驶车队头车到达下游交叉口进口道的时刻，对行驶车队的性能产生相应的影响.低饱和交通状态下，相位差为车队在路段上的平均行驶时间，不随信号周期的变化而变化.当处于近饱和或过饱和时，下游交叉口进口道上可能形成排队车辆，车队在路段上的行驶时间不仅取决于路段长度，还与下游交叉口排队长度有关.因此相邻交叉口合理的相位差)应保证上游交叉口n－1第1个相位绿灯开启后，放行车队头车到达下游交叉口车队尾部的时刻正好等于下游车队的消散波到达该车队尾车的时刻.设置交叉口的直行放行为协调方向，确定相位差时所考虑的排队车辆为协调相位f*开始时下游进口道上的滞留车辆数.根据相邻交叉口时距分析(见图2)为第k个信号周期交叉口n协调相位f*的有效绿灯时间为第k个信号周期第f个相位滞留车辆数传播到上游所需要的时间.要满足上述条件则有以下关系式成立:

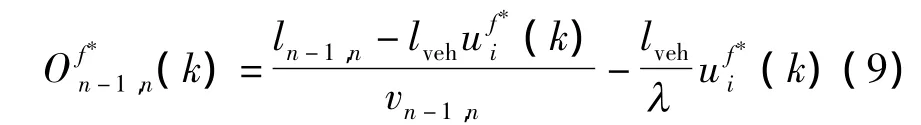
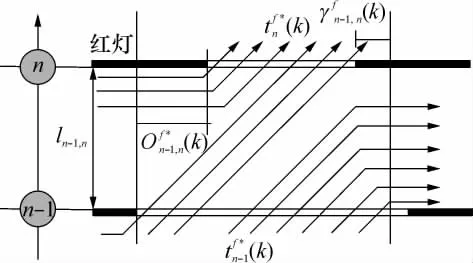
图2 相邻交叉口时距分析Fig.2 Time-space diagram of adjacent intersection

需要注意，式(9)保证了直行方向取得最优的协调控制效果，但对应的左转非协调相位可能并不理想，甚至产生最差协调控制效果.因此，需要综合考虑所有下游交叉口进口道的停车延误情况，对相邻交叉口之间的相对相位差进行全局优化设计.

2.2.2 闭合相位差

在交通区域协调控制中，相邻交叉口n－1与n之间的相位差满足相位差闭合条件:

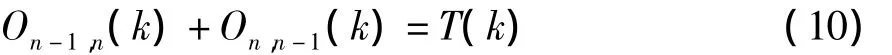
对于构成环路的一组信号控制交叉口，环路各交叉口的相位差之和等于公共信号周期的整数倍:

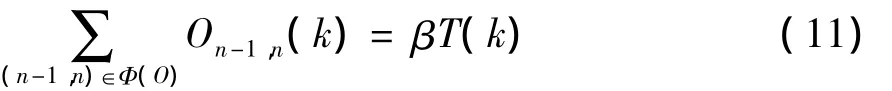
式中:β为整数;Φ(O)为构成环路的相位差的集合.

2.2.3 有效绿灯时间

上游交叉口驶出车流的有效绿灯时间与对应下游交叉口进口道的有效绿灯时间之差，将决定一段时间内路段交通量的积累与消散.下游交叉口排队车辆(k)“溢流”容易造成上游交叉口堵塞，出现“无效绿”现象，因此下游交叉口驶出的车队消散波到达上游交叉口时，上游交叉口放行的直行车辆数必须小于路段的剩余存车能力，相关约束式为

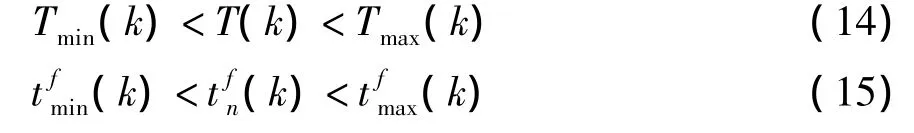
由此建立交通区域协调控制的双层规划模型，其中式(8)为上层规划模型的目标函数，式(2)为下层规划模型的目标函数，其他各式构成约束条件.选取(k)为上层决策变量，(k)为下层决策变量，确定每个周期的绿信比和公共信号周期表示相序选择与优化，适应新的路网交通状况达到区域协调最优化.

2.3 模型求解

上述双层规划问题是一个具有多个下层决策者的NP难解问题.文献［13］中证实，不管模型的目标函数是否为凸规划，BP模型都存在Pareto最优解，且智能算法是解决此类决策问题的最佳策略.遗传算法(GA)是一类基于自然选择机制和遗传变异机制的自适应全局优化概率搜索方法，但局部寻优能力不强，易早熟，不收敛;模拟退火算法(SA)求得全局最小点的概率接近1，能跳出全局最小点，但是寻优过程往往较长.文献［14］中将遗传算法和模拟算法相结合，设计一种遗传模拟退火混合优化策略，取长补短，增强搜索快速收敛于全局最优点的可能.

GA利用SA得到的解作为初始种群，通过复制、交叉、变异等遗传操作使种群得以进化;SA对GA得到的进化种群进一步优化，温度较高时表现出较强的概率突变性，体现为对种群的“粗搜索”，温度较低时演化为局部搜索，体现为对种群的“细搜索”.具体求解模型的算法步骤如下:

步骤1 初始化

(1)确定遗传算法的交叉概率pc、变异概率pm、每一代种群的个体总数H及最大进化代数M.每个个体由e段基因串表示一组信号配时方案.

(2)确定模拟退火算法的内循环次数Z、温度的初始值θ0，令θ=θ0.

步骤2 对每一个个体进行解码，得到对应的相位差初始值，代入求解下层规划获得每一个配时方案对应各交叉口的有效绿灯时间(k)，进而求解上层目标函数值¯Q，计算各个体(k)的适应度.如果gen=M，则适应度最大的染色体即为模型的最优解，算法结束;否则转步骤3.

步骤3 根据适应度分布复制种群U(gen).

步骤4 根据pc和pm分别进行交叉和变异，令gen=gen+1，得到新种群U(gen)，并计算U(gen)中个体的适应度.

步骤5 令τ=1，对种群U(gen)进行模拟退火操作.

(1)若τ=H，转步骤6;否则令循环轮次计数φ=1;

(2)利用状态产生函数产生个体U(gen)的新状态，对新个体进行解码后代入下层规划问题进行计算，从而得到上层规划的目标函数值，并计算其适应度;

(3)以Metropolis概率接受公式接受新个体;

(4)若φ=Z，则令τ=τ+1，转步骤5(1);否则令φ=φ+1，转步骤5(2).

步骤6 退温，令θ=0.5θ，转步骤2.

3 算例分析

文中选择信号配时优化变换方案间隔为30min，方案调整的幅度小，交通流状态短时间内就不会发生巨大变化，可避免交通流的干扰.需要解决的问题是，在一定的约束条件下，如何在保证每个交叉口交通畅通的前提下提高交叉口之间协调控制效果以增加整个路网的通行能力.

为验证文中提出的模型和算法的有效性，用国际上通用的标准测试网络——Sioux Falls网络进行优化计算，利用Matlab遗传算法工具箱编制整个控制算法程序，并与美国广泛应用的Transyt进行仿真比较.假设经过协调控制子区划分的区域网络如图3中虚线框所示，①－[14]代表交叉口，A－J代表区域输入流量的各个边界节点，线段1－40代表内部线段，线段41－70代表边界线段，十字交叉口采用标准的四相位控制，丁字交叉口采用三相位控制，初始相序如图4所示.交叉口各进口道饱和流量s= 1800辆/h，行驶速度为40 km/h，近饱和与过饱和两种状态下的交通需求量如表1所示，设置左转、直行和右转的交通流量分别为25%、60%和15%.周期时长最大值Tmax=150s、最小值Tmin=30s，最小绿灯时间=10s，最大绿灯时间=80s，种群大小为100，终止进化代数为200，交叉概率pc=0.8，变异概率pm=0.1.决策变量为168个为6× 4+8×3=48个，采用实数编码的染色体为100× 216矩阵.

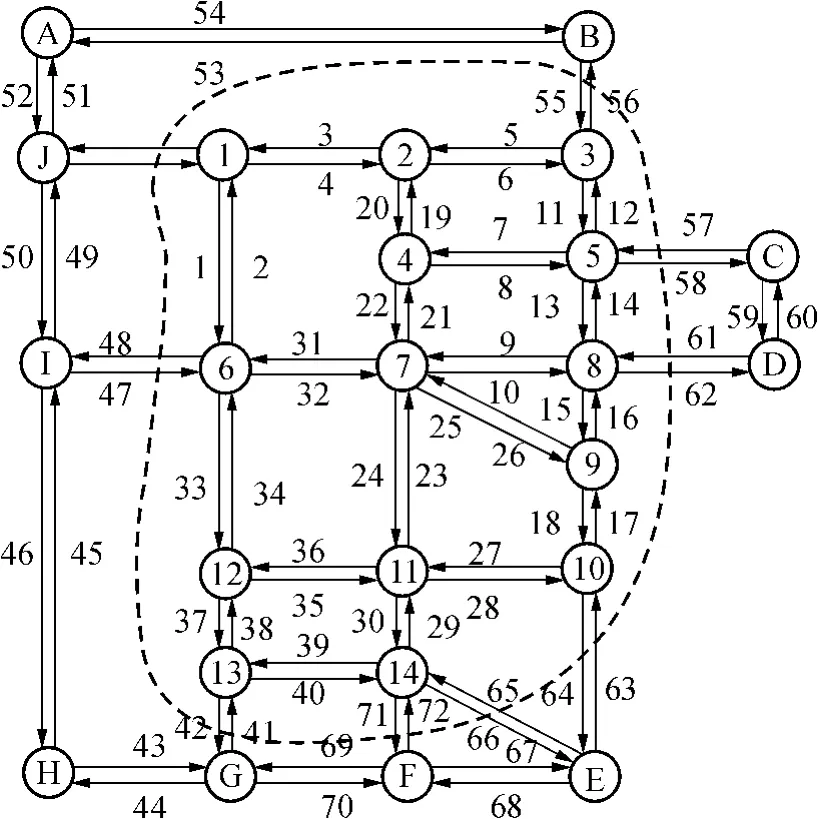
图3 基于Sioux Falls网络的协调控制子区Fig.3 Subarea division of coordinated control based on Sioux Falls network

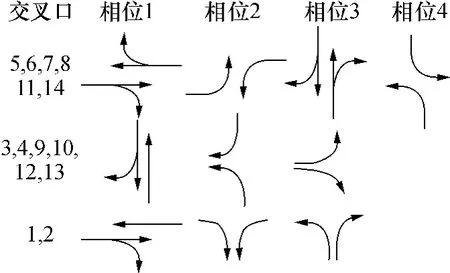
图4 交叉口初始相序设置Fig.4 Initial phase sequences of intersections

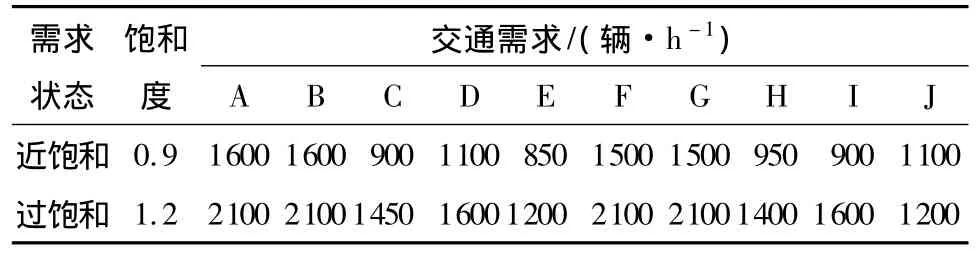
表1 不同交通状态下的区域交通需求Table 1 Area traffic demand in different scenarios

为验证交通信号区域协调控制双层规划模型的合理性，利用德国PTV公司开发的微观交通仿真软件VISSIM5.0，针对BP模型和TRANSYT模型的最佳信号配时方案分别进行仿真分析与对比评价，仿真结果如表2所示.在近饱和交通状态下，BP模型的公共信号周期比TRANSYTF小，总延误时间和总输出交通量相近，性能没有大幅度提高，总延误时间仅提高2%，总输出车辆仅提高0.7%.但在过饱和交通状态下，BP模型的总延误时间缩短15.2%，总输出交通流量增加8.7%.相对于近饱和交通状态下，性能大大提高.TRANSYT模型为提高通行能力选择相对较大的公共信号周期，反而因为高到达率使交叉口发生交通堵塞的可能性提高，这与TRANSYT只适用于低饱和交通状态的信号配时相吻合.表2同时反映了交通拥堵对交叉口总延误时间的影响，在不发生拥堵时交叉口总延误时间为7253.2s，而在高峰拥挤时段用户的出行时间将增加到原来的3倍左右.

表2 VISSIM仿真结果比较Table 2 Comparison of VISSIM simulation results

相位差的选取对交叉口性能有重要影响，过饱和条件下交叉口7的延误时间和输出流量随相位差的变化趋势如图5所示.当相位差为30s时，最小延误时间为2400 s，输出交通量只有1200辆，并非全局最优值;保持相位差不变增大输出交通量时，交叉口延误时间迅速增加到最高点3800 s.权衡上下层目标函数，最优相位差选择在70s处，此时虽然延误时间并非最小值，但输出流量比较多.对交叉口的延误时间进行深入分析发现，BP模型与TRANSYT模型在各交叉口的延误时间曲线大致相同，如图6所示，协调控制子区中心交叉口7的延误时间最大，其次为交叉口14和8，这说明各交通信号控制策略选取的关键交叉口是一致的.

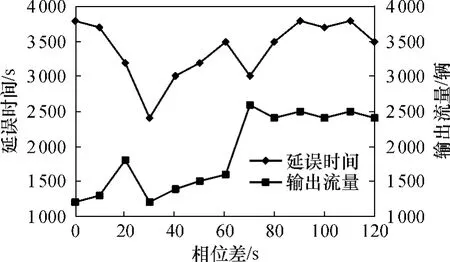
图5 交叉口7性能指标随相位差的变化Fig.5 Variations of performance index with phase difference at intersection 7

图6 各交叉口延误时间比较Fig.6 Comparison of delay time among all intersections

4 结语

如何在交通出行特征的基础上实施有效的交通信号控制配时策略是交通管理部门亟需解决的问题.文中在协调控制子区划分的基础上，提出以区域整体输出总流量最大为上层目标的双层规划模型，并进一步考虑了排队长度、路段交通量、相邻交叉口相位差闭合等约束对区域协调效果的影响.结合BP模型的非凸性特点，提出基于遗传－模拟退火算法的GASA混合优化策略.仿真结果表明，过饱和状态下，BP模型在车辆延误、系统总输出交通量等性能指标方面均显著优于TRANSYT模型，为解决交通拥堵问题提供了新方向.

［1］ 卢凯，徐建闽，郑淑鉴.相邻交叉口关联度分析及其应用［J］.华南理工大学学报:自然科学版，2009，37 (11):37-42.Lu Kai，Xu Jian-min，Zheng Shu-jian.Correlation degree analysis of neighboring intersections and its application［J］.Journal of South China University of Technology: Natural Science Edition，2009，37(11):37-42.

［2］ 卢凯，徐建闽.干道协调控制相位差模型及其优化方法［J］.中国公路学报，2008，21(1):83-88.Lu Kai，Xu Jian-min.Offset model for arterial road coordinate control and its optimization method［J］.China Journal of Highway and Transport，2008，21(1):83-88.

［3］ 万绪军，陆化普.线控系统中相位差优化模型的研究［J］.中国公路学报，2001，14(2):99-102.Wan Xu-jun，Lu Hua-pu.An optimal offset model for artery traffic signal control system［J］.China Journal of Highway and Transport，2001，14(2):99-102.

［4］ Chang Tang-Hsien，Sun Guey-Yin.Modeling and optimization of an oversaturated signalized network［J］.Transportation Research Part B:Methodological，2004，38:687-707.

［5］ 刘灿齐.城市道路网络交通信号协调控制的优化［J］.同济大学学报:自然科学版，2004，32(8):1000-1004.Liu Can-qi.Integral optimizing method of traffic signal on network of urban road［J］.Journal of Tongji University: Natural Science，2004，32(8):1000-1004.

［6］ 承向军，杜鹏，杨肇夏.基于多智能体的分布式交通信号协调控制方法［J］.系统工程理论与实践，2005，25 (8):130-135.Cheng Xiang-jun，Du Peng，Yang Zhao-xia.A distributed and coordinated traffic signal control approach based on multi-agent system［J］.Systems Engineering Theory＆Practice，2005，25(8):130-135.

［7］ 李水友，刘智勇.基于D-S证据理论的区域交通自适应协调控制［J］.控制理论与应用，2005，22(1):157-160.Li Shui-you，Liu Zhi-yong.D-S evidence theory based adaptive control method for urban traffic network signal［J］.Control Theory＆Applications，2005，22(1):157-160.

［8］ 张辉，杨玉珍，李振龙.基于分布式Q学习的区域交通协调控制的研究［J］.武汉理工大学学报，2007，31 (6):1121-1124.Zhang Hui，Yang Yu-zhen，Li Zhen-long.Urban traffic coordination control based on distributed Q-learning［J］.Journal of Wuhan University of Technology，2007，31(6): 1121-1124.

［9］ 刘智勇，李水友.基于免疫遗传算法的区域交通自适应协调控制［J］.控制理论与应用，2006，23(1):119-125.Liu Zhi-yong，Li Shui-you.Immunity genetic algorithms based adaptive control method for urban traffic network signal［J］.Control Theory＆Applications，2006，23(1): 119-125.

［10］ Girianna Montty，Benekohal Rahim F.Using genetic algorithms to design signal coordination for oversaturated networks［J］.Intelligent Transportation System，2004，8 (2):117-129.

［11］ Lu Jie，Shi Cheng-gen，Zhang Guang-quan.On bilevel multi-follower decision making:general framework and solutions［J］.Information Sciences，2006，176:1607-1627.

［12］ Dempe S.Annotated bibliography on bi-level programming and mathematical programs with equilibrium constraints［J］.Optimization，2003，52(3):333-359.

［13］ 腾春贤，李智慧.二层规划的理论与应用［M］.北京:科学出版社，2002:86-100.

［14］ 刘伟铭，姜山.基于GASA混合优化策略的双层规划模型求解算法研究［J］.土木工程学报，2003，36 (7):27-32.Liu Wei-ming，Jiang Shan.GASA hybrid optimization strategy for bi-level programming models［J］.China Civil Engineering Journal，2003，36(7):27-32.