基于直接功率控制的双PWM变频调速系统*

汪万伟 尹华杰 管霖

(华南理工大学电力学院，广东广州510640)

目前，变频器已广泛应用于工农业生产的各个领域，用于驱动电机或作为变频电源.通用变频器大多采用二极管整流的电压型AC-DC-AC拓扑结构，不能直接用于需要快速起、制动和频繁正、反转的调速场合，因为二极管整流电路的能量传输是不可逆的［1］.

由脉宽调制(PWM)整流器和PWM逆变器构成的双PWM可逆整流控制系统(如图1所示)无需增加任何附加电路，只需通过对变换器的开关器件按照一定的控制规律进行通断控制，即可消除网侧谐波污染，实现高功率因子及能量双向流动，方便电机四象限运行［2-3］，并且电机动态响应时间短，是高质量能量回馈技术的最新技术之一.

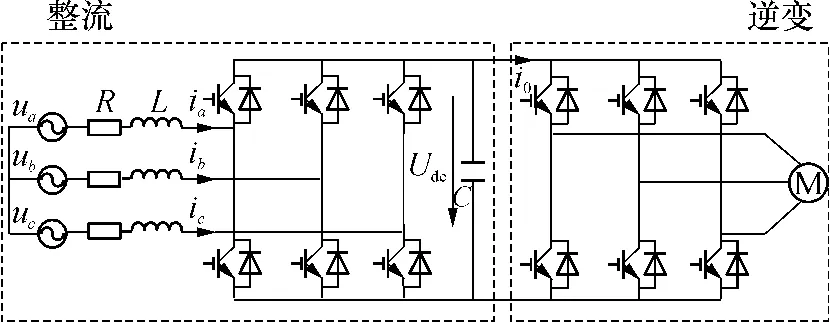
图1 主电路拓扑图Fig.1 Main circuit topology

现行的电压型PWM整流器控制策略主要分为3类，即间接电流控制［4-5］、直接电流控制［6］和直接功率控制［7-8］.其中，间接电流控制的动态特性较差，而直接电流控制的控制结构则较复杂，参数整定困难.不仅如此，在由电流控制策略构建的双PWM控制方案中，为了在不加大电容的情况下避免大的直流电压波动，都需要对整流器和逆变器进行协调控制［9-10］，这更增加了系统的复杂程度.

为了克服上述缺点，文中提出了基于直接功率控制的双PWM变频调速方案，网侧整流器采用基于瞬时功率理论的直接功率控制(DPC)策略.并基于Matlab/Simulink对该控制方案进行了仿真，验证了其可行性.

1 双PWM变频调速系统网侧整流器的直接功率控制模型

1.1 网侧整流器的功率控制模型

三相电压型PWM整流器的主电路拓扑结构如图1左侧虚线框所示，网侧电路采用三相对称的无中线连接方式，功率开关管桥路采用三相桥式全控整流电路、IGBT(Insulated Gate Bipolar Transistor)和续流二极管并联作为桥臂开关器件.

对于图1中网侧的三相桥式PWM变流器，定义三相桥臂开关函数Sa、Sb、Sc为:

可根据图1得到三相PWM整流器在三相静止坐标系下的方程:

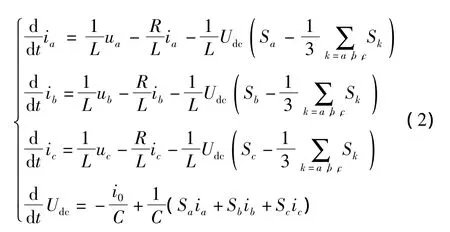
式中:ux为各相网压;ix为各相电流;i0为负载电流，并以整流方向为正;x=a，b，c;L、R为交流侧的滤波电感和阻抗;Udc为直流输出电压.将三相静止坐标系下的变量变化到两相旋转d-q坐标系下，其数学模型为

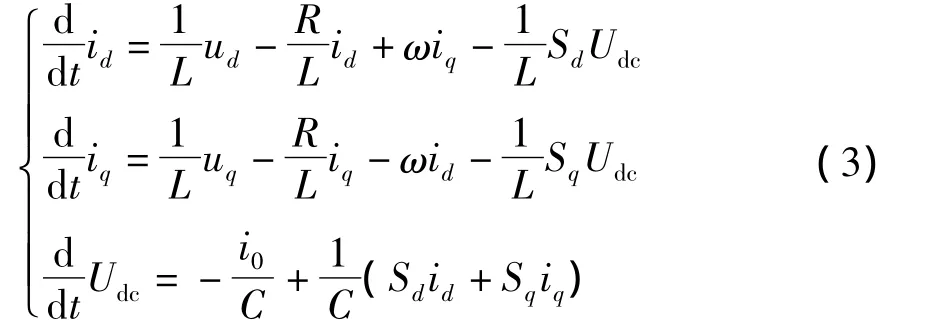
式中:Sd、Sq分别为整流桥的d-q坐标系下的开关函数;ud、uq和id、iq分别为网侧电动势和电流的d、q分量;ω为角频率.

可以用有功功率平衡方程来描述直流侧的电压动态过程.交流侧输入有功功率用Pac表示，直流侧吸收的有功功率用Pdc表示，则有

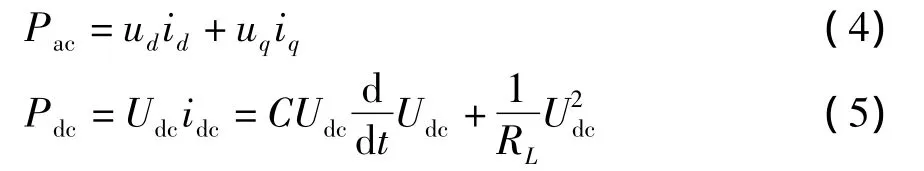
式中:RL为负载等效电阻;CUdcdUdc/dt为直流侧支撑电容瞬时吸收或释放的能量，U2dc/RL为负载瞬时吸收或释放的能量.

根据功率平衡原理，整流器的输入功率等于其瞬时输出功率，Pac和Pdc的关系为

式中:Ploss为整流器输入电感的等效电阻及开关管的损耗.如果不计损耗，可得

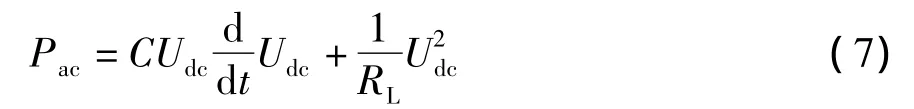
交流侧的无功qac=uqid－udiq，由于uq=0，即

联立式(3)、(4)和式(8)，可得到以Pac和qac为变量的功率控制模型:

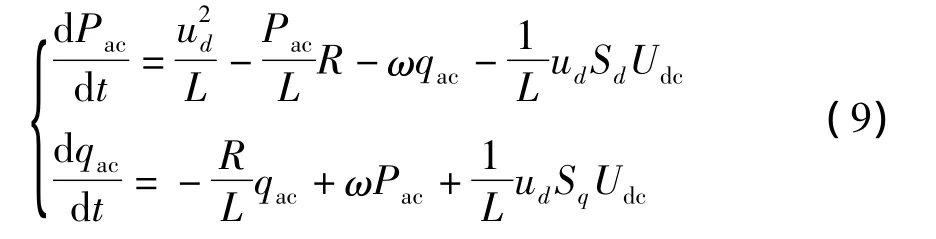
控制系统的控制目标是使Pac收敛于Pdc(即，qac收敛于=0.由式(5)及(9)，采用电压定向直接功率控制(VO-DPC)策略的控制系统框图如图2所示.

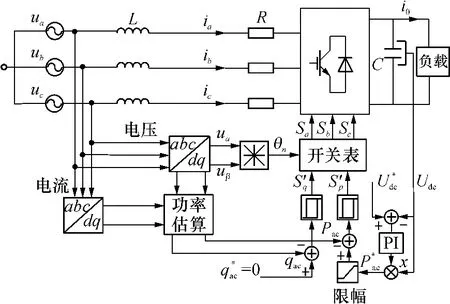
图2 PWM整流器直接功率控制系统框图Fig.2 Block diagram of direct power control system for PWM rectifier

该控制系统具有一个直流电压外环和一个功率内环.电压外环采用PI控制器产生有功给定，功率内环则采用滞环比较器，以迫使实际有功跟上该给定.

1.2 开关表的确定

开关表是关于电压向量V0－V7的选择表.由两相静止坐标系下的电网电压uα、uβ计算出u的幅角，开关表就是通过θ所在θ－θn112的区间来确定的［11］，如图3所示.当uα为正值时，θn可直接由，通过判断θ的值来确定其

n在象限中的位置;当uα为负值时，通过判断θn=π+的值来判断u的位置.

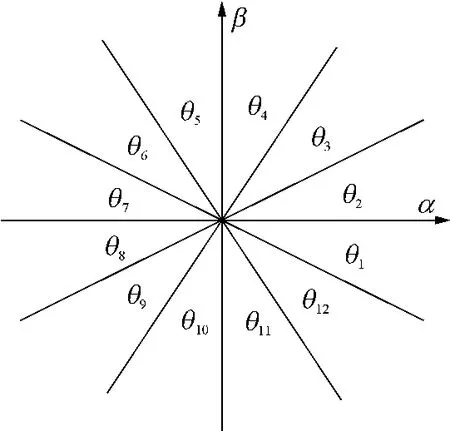
图3 α－β坐标系下的电压空间划分Fig.3 Space vector of voltage in α－β coordinate system

当估算的有功功率Pac与有功功率的参考值之差超过滞环宽度Hp时，关闭有功功率开关，即有功功率开关函数S'p=0;反过来，当有功功率的参考值与有功功率的预估值Pac之差超过滞环宽度Hp时，打开有功功率开关，即有功功率开关函数S'p=1.同理，得出如下瞬时有功功率和无功功率的开关函数:

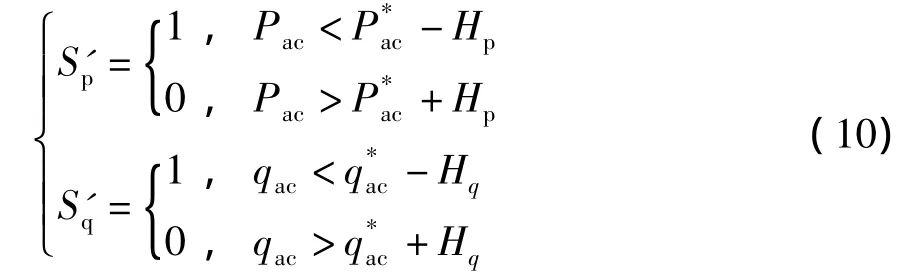
开关表由式(10)及θn确定:Sa、Sb、Sc的值取决于所需的ur，ur为离散值U0，U1，…，U7，其值由Sa、Sb、Sc和Udc决定，即SaSbSc=000－111对应于U0－U7，即U0(000)、U1(100)、U2(110)、U3(010)、U4(011)、U5(001)、U6(101)、U7(111)，分布如图4所示.例如，当u在θ1区域时，Ir为与相对应的电流向量，当 i=I时，I滞后并小于 Ir，由 Pac= iαuα+iβuβ，qac=iβuα－iαuβ可知，P，即S'p=1，S'q=0，则选择ur使i趋近于Ir，即Pac趋近于、qac趋近于.忽略网侧电阻R的影响，由式(2)得

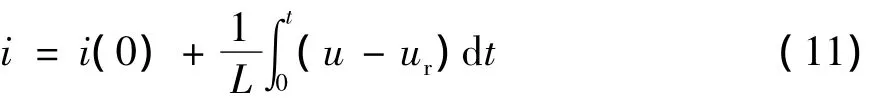
式中:i(0)=I，ur选择U6(101)，由图4，i将沿着u－ur方向趋近于Ir，则确定SaSbSc=101.同样，i在其它位置可用同样方式进行分析.另外，适当引入零空间向量可以增加功率传输能力.以此确定的开关表如表1所示［12］.

图4 α－β坐标系下电压向量的选取Fig.4 Selection of voltage vector in α－β coordinate system

表1 PWM整流器直接功率控制系统开关表Table 1 Switching table for direct power control of coordinate PWM rectifier

2 双PWM变频调速系统异步电机侧的向量控制系统

向量控制的基本思路是以产生相同的旋转磁动势为准则，将异步电动机在静止三相坐标系上的定子交流电流通过坐标变换等效成同步旋转坐标系上的直流电流分别加以控制，以达到直流电机的控制效果［13-15］.异步电动机在两相同步旋转坐标系上的电压方程为

式中:usd、usq、urd、urq分别为定子和转子电压的d、q分量;isd、isq、ird、irq分别为定子和转子电流的d、q分量;ψsd、ψsq、ψrd、ψrq、ψr分别为定子和转子磁链的d、q分量及转子磁链;Ls、Lr、Lm分别为定子和转子的自感及互感;Rs、Rr分别为定子和转子绕组电阻; ωe、ωr、ωs为同步角速度、转子角速度、转差角速度，ωs=ωe－ωr;p为微分操作数.

磁链方程为

转矩方程为

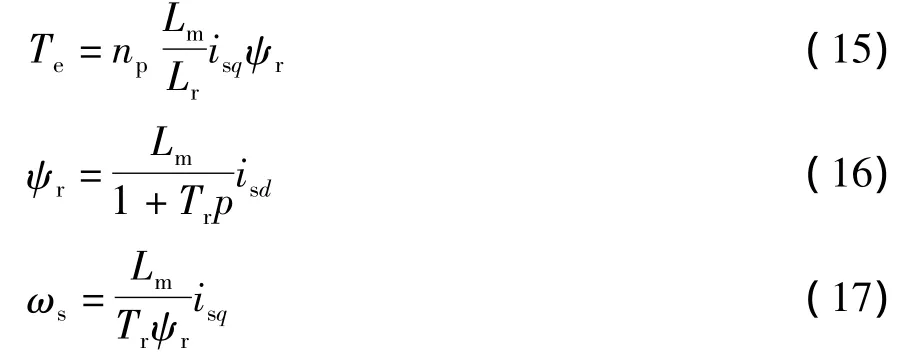
式中:Tr为转子时间常数;Te为电磁转矩;np为极对数.

为了减小电机的转矩脉动，改善电机的运行性能，文中采用SVPWM调制方案，以使异步电机的磁链空间向量逼近圆形.图5所示为向量控制系统的结构框图.图中，带*的量为给定量.isa、isb、isc为三相定子电流;isα、isβ为定子电流的α、β分量;θ为转子磁链的位置角;为定子电压转矩分量和励磁分量的给定;为定子电压α、β分量的给定.

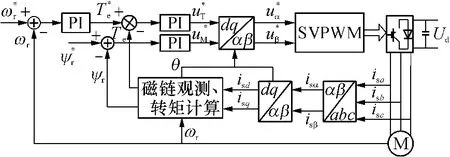
图5 异步电机向量控制框图Fig.5 Vector control system of induction motor

3 双PWM变频调速系统仿真及分析

根据图2和图3所示的控制框图，在Matlab/ Simulink环境中建立了仿真模型.仿真所用的参数为:网侧相电压有效值220 V，频率50 Hz，网侧电阻0.1Ω、电感4mH，直流电压设定600 V，直流侧电容2000μF;三相异步电动机为2对极，额定电压380V，频率50Hz，额定功率15kW，转子电阻0.3017Ω，定子电阻0.525 7 Ω，转子漏感0.004 9 H，定子漏感0.0049H，互感0.1166 H，转动惯量0.102 kg·m2，转子磁链给定为1Wb，SVPWM的开关频率为10kHz.

仿真波形如图6所示，其中图6(c)和6(d)中的虚线对应于转速给定和负载转矩给定(实际大小是该虚线的2倍，以便识别)，图6(b)中的放大图，为网侧电流电压波形图.图中，在0.8～1.3 s和2.8～3.3s范围内，电机稳定运行于第一、三象限，在1.8～2.3s和3.8～4.2s，电机稳定运行于二、四象限.

从图6(a)可以看出，直接功率控制的整流器具有良好的动态性能力和抗干扰能力，负载扰动对其直流电压的影响很小，且迅速回到稳定状态.

由图6(b)可知，当电机运行于一、三象限时，能量由电网向电机传送，网侧电压、电流同相位;当电机运行于二、四象限时，能量馈送电网，网侧电压、电流反相位.从局部放大图可见，双PWM系统不仅实现了单位功率因子能量双向流动，而且使网侧电流谐波含量较小，大大降低了对电网的污染.

图6(c)－6(e)反映了电机侧的波形状况，表明电机的转速、转矩具有良好的跟随性，稳定迅速，纹波非常小.定子电流的正弦度非常优异.

图6(f)－6(h)表明，交流侧提供(吸收)的有功功率全为直流侧所利用(提供)，且无功分量相对于有功分量基本为0，实现了单位功率因子能量双向传输，从而大大减小了网侧的谐波污染.

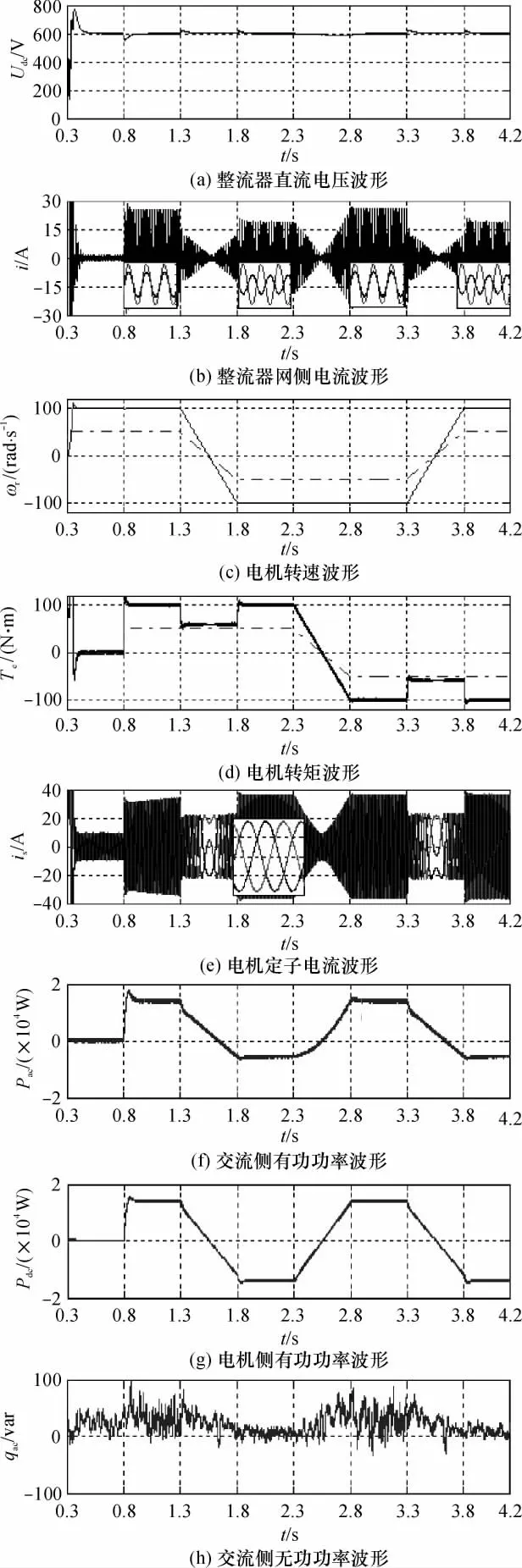
图6 双PWM仿真波形图Fig.6 Simulation waveforms of dual-PWM control system

为了验证直接功率控制策略具有良好的动态性能和抗扰动能力，文中还进行了无协调控制环节的直接电流控制的双PWM变频调速的仿真，其整流侧直流电压波形如图7所示，从图7中可以看出，此控制策略的直流电压波形对负载的扰动较为敏感，动态响应能力要次于上述的直接功率控制策略.

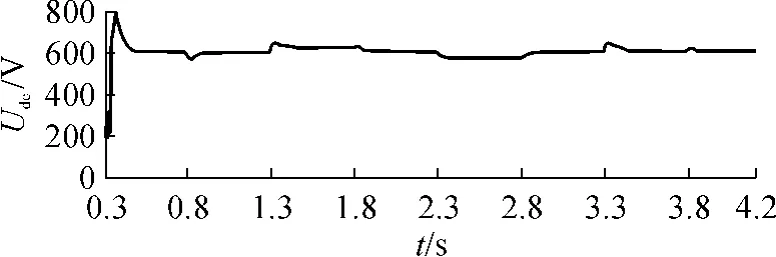
图7 直接电流控制的直流电压波形Fig.7 DC-bus waveform of direct current control system

4 结语

文中在详细分析双PWM变频调速系统数学模型的基础上，研究了双PWM的直接功率控制方案，此方案不需要附加双PWM的协调控制环节，从而使控制更加简便.仿真结果表明，在运行过程中，交流侧提供的有功始终接近于电机所需的有功，而交流侧的无功则接近0，从而实现了单位功率因数的能量传递，提高了电能的利用效率，也大大减少了谐波对电网的污染.

［1］ 张崇巍，张兴.PWM整流器及其控制［M］.北京:机械工业出版社，2003.

［2］ Lee Ke-Yen，Wu Yue-Lin，Lai Yen-Shin.Novel bidirectional three-phase rectifier without using DC-link current sensor［C］∥Proceedings of the 37th IEEE Power Electronics Specialists Conference.Korea:IEEE，2006:3302-3306.

［3］ Jung Jinhwan，Lim Sunkyoung，Nam Kwanghee.A feedback linearizing control scheme for a PWM converter-inverter having a very small DC-link capacitor［J］.IEEE Transactions on Industry Applications，1999，35(5): 1124-1131.

［4］ Kim Hyosung，Yu Taesik，Choi Sewan.Indirect current control algorithm for utility interactive inverters in distributed generation systems［J］.IEEE Transactions on Power Electronics，2008，23(3):1342-1347.

［5］ 李玉玲，鲍建宇，张仲超.间接电流控制可调功率因子电流型PWM变流器［J］.中国电机工程学报，2007，27 (1):49-53.Li Yu-ling，Bao Jian-yu，Zhang Zhong-chao.Indirect current control adjustable power factor current source PWM converter［J］.Proceedings of the CSEE，2007，27(1): 49-53.

［6］ Cichowlas M，Kamierkowski M P.Comparison of current control techniques for PWM rectifiers［C］∥Proceedings of the 2002 IEEE International symposium on Industrial Electronics.L'Aquila:IEEE，2002:1259-1263.

［7］ 王久和，李华德，王立明.电压型PWM整流器直接功率控制系统［J］.中国电机工程学报，2006，26(18): 54-60.Wang Jiu-he，Li Hua-de，Wang Li-ming.Direct power control system of three phase boost type PWM rectifiers［J］.Proceedings of the CSEE，2006，26(18):54-60.

［8］ Baktash A，Vahedi A，Masoum M A S.Improved switching table for direct power control of three-phase PWM rectifier［C］∥Proceedings of Power Engineering Conference CAUPE(2007).Australasia:IEEE，2007:1-5.

［9］ Tallam R M，Naik R，Gasperi M L.Practical issues in the design of active rectifiers for AC drives with reduced DC-link capacitance［C］∥Conference Record of the 2003 IEEE Industry Applications Conference，38th IAS Annual Meeting.Salt Lake City:IEEE，2003:1538-1545.

［10］ Hur Namho，Jung Jinhwan，Nam Kwanghee.A fast dynamic DC-link power-balancing scheme for a PWM converter-inverter system［J］.IEEE Transactions on Industrial Electronics，2001，48(4):794-803.

［11］ Noguchi Toshihiko，Nakatomi Somei，Takeuchi Daisuke.Direct power control based matrix converter and its operation characteristics［C］∥Proceedings of the 32nd Annual Conference on IEEE Industrial Electronics.Paris:IEEE，2006:1872-1877.

［12］ Vazquez S，Sanchez J A，Carrasco J M.A model-based direct power control for three-phase power converters［J］.IEEE Transactions on Industrial Electronics，2008，55(4):1647-1657.

［13］ 贺晓蓉，刘述喜，陈新岗.基于SVPWM的异步电机矢量控制系统的仿真［J］.计算机仿真，2007，24(4): 322-325.He Xiao-rong，Liu Shu-xi，Chen Xin-gang.Simulation of vector control system of induction machine base on SVPWM［J］.Computer Simulation，2007，24(4):322-325.

［14］ 朝泽云，康勇，钟和清，等.异步电机矢量控制系统的建模与仿真［J］.电机与控制应用，2007，34(3): 11-14.Chao Ze-yun，Kang Yong，Zhong He-qing，et al.Modeling and simulation of asynchronousmotor vector control system［J］.Electric Machines＆Control Application，2007，34(3):11-14.

［15］ 叶斌.电力电子运用技术［M］.北京:清华大学出版社，2006.