基于能量反应谱的结构能量反应竖向分布研究

常 磊， 叶献国， 潘文军

(合肥工业大学土木与水利工程学院，安徽合肥 230009)

输入到结构的地震能量与结构特性有关，弹性及弹塑性下的能量反应不尽相同。弹性下其总输入能可根据结构自振周期和振型质量方便地计算，而弹塑性下的能量输入却因结构进入塑性状态的深浅以及结构滞回特性而异，且可能与弹性下的总输入能有较大的差距[1，2]，因此弹塑性下结构的总能量反应仍然难以估计。

能量在结构竖向的分布受结构竖向特性影响，如结构竖向刚度及其分布等相关参数。弹塑性状态下，为简化研究，学者们曾假定滞回耗能在楼层间呈倒三角形或梯形分布[3，4]。但在罕遇地震下，对具有复杂滞回模型的结构模型，其滞回耗能分布并不具有简单的线性特征:对框架结构，滞回耗能在层间呈近梯形分布;而对框剪结构，滞回耗能呈严重的非线性分布[5]。因此，从数值模拟上来分析耗能分布以期获得普适性的规律显得较为困难。为研究地震能量在结构中的竖向分布特征，从结构弹性能量反应着手显得比较方便，可避开弹塑性下诸多参数的复杂影响。此外，由于结构及构件的损伤破坏与其耗能密切相关，研究能量在结构内部的分布规律非常有意义。研究表明，可建立基于结构构件层次的能量不平衡方程，方程的不平衡性是地震能量在结构内部得以传递和耗散的保证[6]。基于构件层次定义的各能量项具有明显的物理意义，且对弹性状态下的结构，可用一种模态非耦合的形式去计算楼层能量，计算方便且精度高[7]，但此方法的适用性研究报道很少。

本文对楼层能量反应的模态非耦合计算方法进行了参数及适用性研究，推导了应用能量反应谱法后结构弹性能量反应沿竖向分布的表达式，并阐述了结构振型及结构刚度振型在楼层能量竖向分布中的意义。

1 楼层能量模态非耦合计算的适用性

文献[7]给出了弹性楼层能量反应的模态非耦合简化计算式(变形能、动能、阻尼耗能及总输入能分别见(1)～(4)式)，但未对其适用性进行研究。

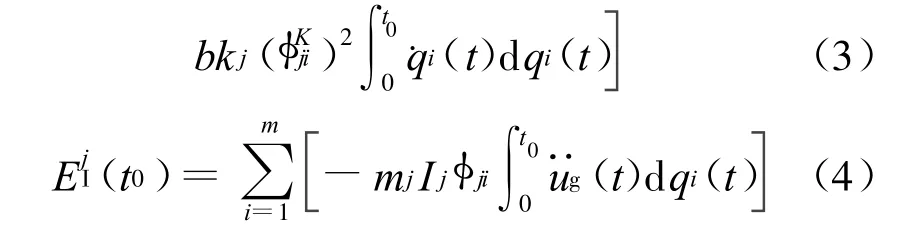
其中，(3)式及本文所有算例均选用Ray leigh阻尼形式[8];a、b为对应的质量和刚度矩阵系数(算例中1、2阶阻尼比均为0.02);kj、mj、¨ug(t)分别为结构第j楼层的刚度、质量及t时地震输入;qi、φji及φK

ji分别为结构第i振型坐标和振型以及第i刚度振型在j楼层的分量;列向量元素Ij为0或1。按文献[7]，楼层动能和变形能按简化式计算时有一定误差，因此针对动能和变形能，本文考虑了2种不同的方法以验证此简化式。

(1)方法1。选用文献[7]中算例，取1940年美国Imperial Valley Earthquake记录之一的南北分量作为地震输入(峰值加速度341.7 cm/s2，总持时53.74 s)。按照傅里叶变换理论，修改原记录的时间间隔d t，得到具有不同卓越周期(Predominant Period，简称PP)的地震记录10条，且使各PP接近结构自振周期T或介于其中两者之间，见表1所列。

随机选择的5条天然地震动记录特性见表2所列。

按(1)式、(2)式计算能量，并与准确值(一般的数值积分法计算结果)对比计算相对误差，结果如图1所示，动能和变形能计算相对误差分别在10-13和10-7量级，可见误差很小。

表1 修改所得10条地震动记录特性s

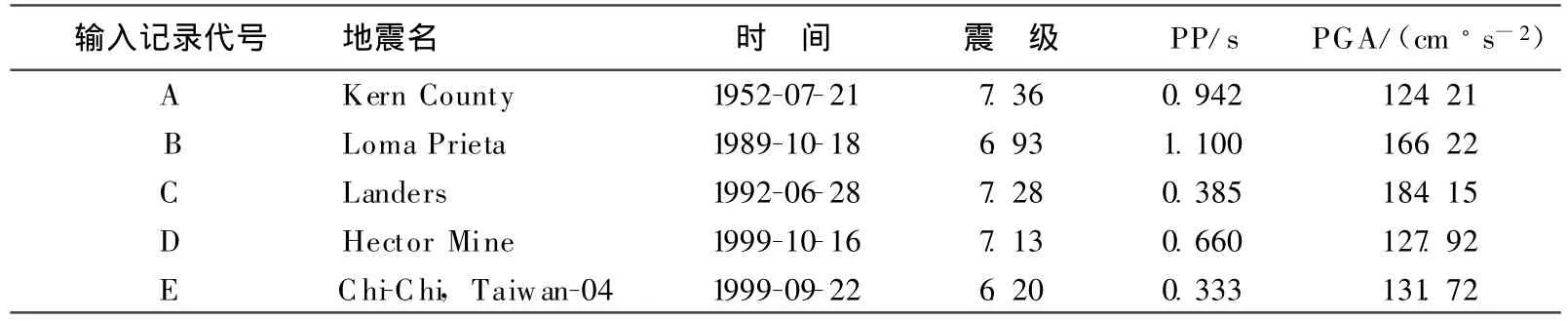
表2 随机选择的5条天然地震动记录特性

(2)方法2。记文献[7]的算例为结构Ⅰ，假定各层质量和刚度分别为10.2×104kg和3.5× 108N/m，得结构Ⅱ(其各阶频率分布较Ⅰ密集)。从太平洋地震研究中心(The Pacific Earthquake Engineering Research Center，简称PEER)随机选择5次不同地震中记录的水平分量之一作为地震输入，仿方法1计算能量相对误差。2种结构动能及变形能相对误差时程图，如图2所示。研究发现，动能和变形能的相对误差仍然很小，分别在10-12和10-7量级。考虑选择地震动的随机性，可以用简化计算公式(1)～(4)式计算糖葫芦串型建筑结构 的弹性楼层能量的准确性。

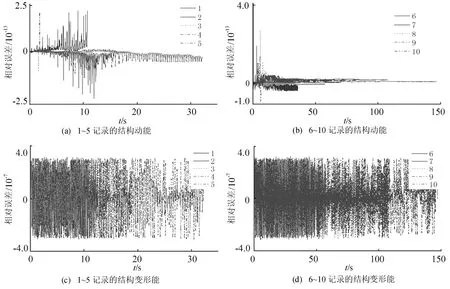
图1 各记录下结构动能及变形能相对误差时程图

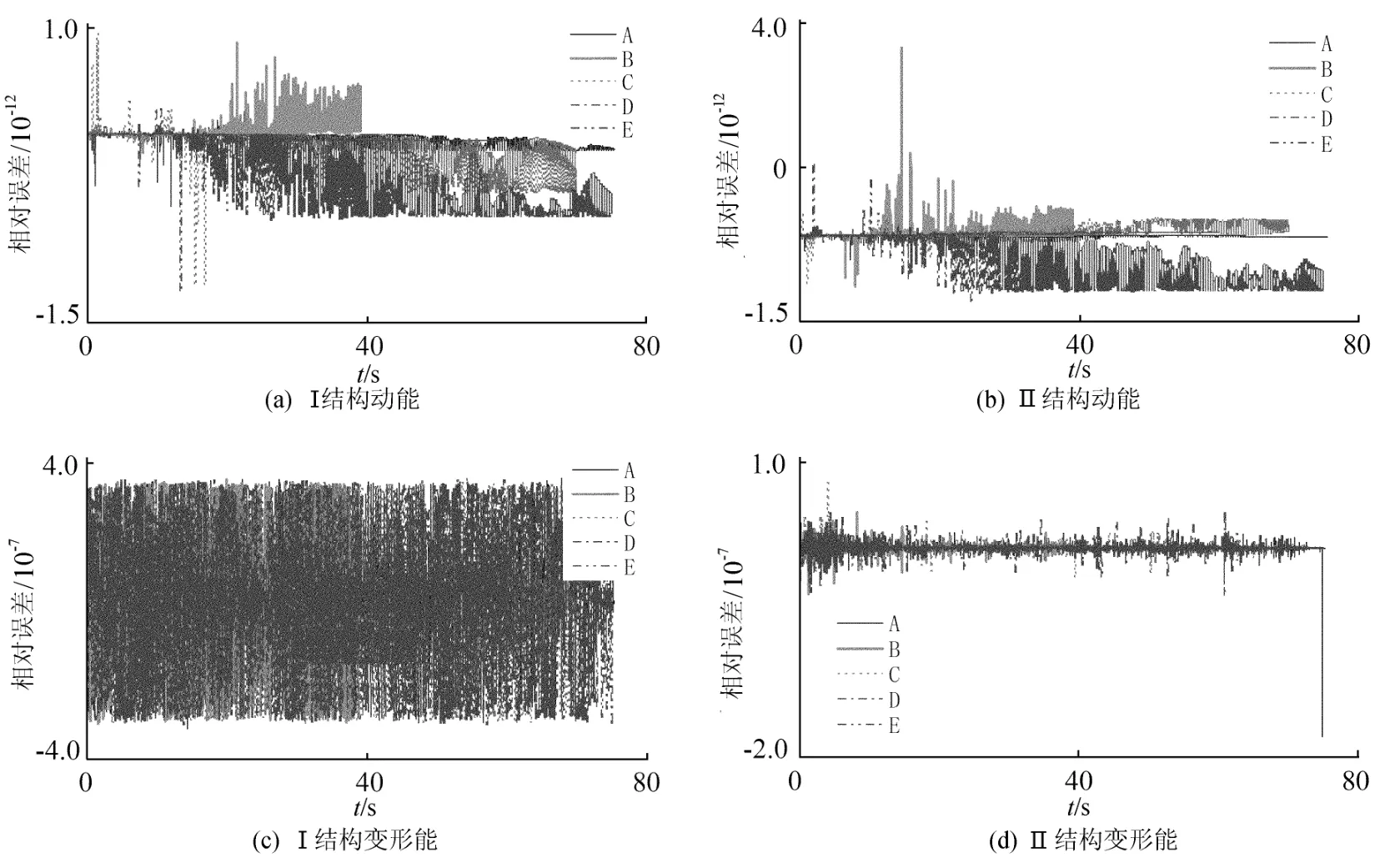
图2 2种结构动能及变形能相对误差时程图

2 在楼层能量反应中应用能量反应谱

弹性下，考虑设计需求，可建立能量反应谱[9]，并已成功应用于结构总能量反应计算中[2]。考虑在结构能量分布研究中，学术界侧重于研究输入能及变形能的分布规律，本文针对(1)式和(4)式分别推导出基于能量反应谱的楼层变形能和输入能的表达式。按(5)式计算SDOF各能量的最大反应，可得在阻尼比ζi、频率 ωi(ωi= 2π/Ti)下动能、阻尼耗能、变形能及总输入能反应谱值分别为eKi(ζi，ωi)、eDi(ζi，ωi)、eEi(ζi，ωi)和e I i(ζi，ωi)。经推导可得第j楼层的楼层输入能和变形能最大值的表达式为:

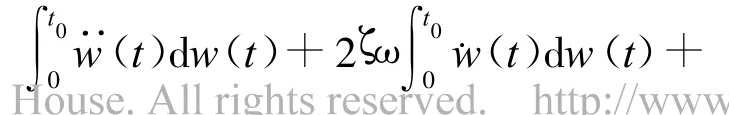
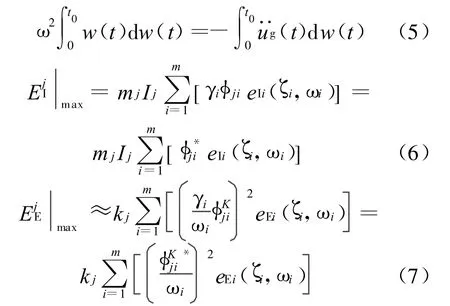
其中，γi为第i振型参与系数，若调整各振型使其为1，则(6)、(7)式有更简化的表达式(第2等号)，记此时的振型为一致振型φ*ji和一致刚度振型φK*ji。

3 算例分析

选取文献[2]中A记录，对结构Ⅰ(其一致振型及一致刚度振型的平方如图3所示)进行弹性能量反应分析，计算得各楼层输入能及变形能最大值(Ei-FOR和Ee-FOR)。将此结果与采用楼层能量反应谱法((6)式、(7)式)计算的结果(Ei-RSP和Ee-RSP)绘于图4，并进行对比研究。

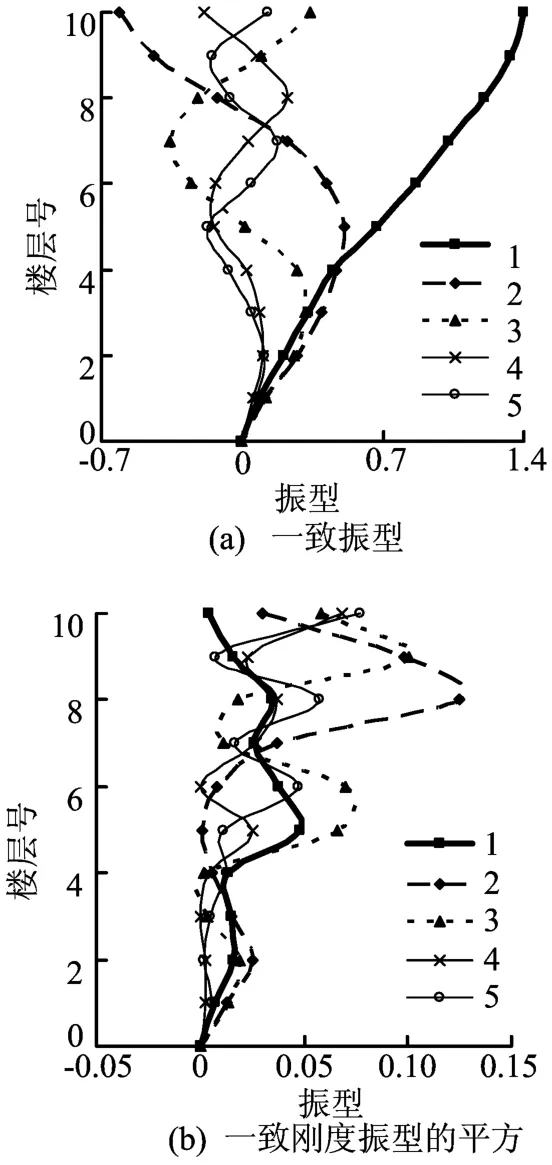
图3 前5阶一致振型和一致刚度振型的平方

首先，由图4a按楼层能量反应谱法计算的楼层能量结果与准确值非常吻合;其次，由于在结构前3阶周期上随着阶数增大A记录的反应谱值(输入能及变形能)以0.1倍的速度递减，使得第1振型为结构能量反应的控制振型，且楼层变形能估计式((7)式)中高阶振型贡献量又被ω2除，使其贡献更小，使得按第1阶振型估计时，变形能要比输入能更准确，如图4b所示。因此，(6)式、(7)式可以很好地估计楼层能量反应最大值。

图4 楼层能量反应谱法与准确结果对比

避开算例，分析(6)式、(7)式的组成:若结构第1阶振型为控制振型而忽略高阶振型，且结构楼层刚度和质量分布均匀(即一般建筑结构)，则楼层输入能和变形能反应将与结构第1阶振型和第1阶刚度振型平方成比例。因此，从能量角度，对比图3中第1阶各振型和图4，可得结构一致振型和一致刚度振型的平方分别反映了楼层输入能和楼层变形能沿层分布特征。

4 结束语

本文针对糖葫芦串模型，首先通过大量算例探讨了楼层弹性能量反应的振型非耦合简化计算方法的适用性;然后基于能量反应谱的概念，推导出楼层能量反应最大值的表达式，实现了能量反应谱法在楼层能量反应中的应用。

分析表明，不同层模型结构在不同地震记录作用下，简化的楼层能量反应计算误差非常小，可以忽略，用能量反应谱可以很好地估计各层的楼层能量反应最大值。针对输入能和楼层变形能，本文给出了算例分析和深入探讨，结合提出的结构一致振型矩阵及一致刚度振型矩阵概念，楼层能量反应谱法的表达式较简单，且此2种振型可分别反映楼层输入能和楼层变形能的竖向分布规律。

对可简化为层模型的普通建筑结构(即质量和刚度沿楼层分布均匀)，当第1振型为控制振型时，弹性楼层输入能和弹性楼层变形能分别按结构第1阶(一致)振型及第1阶(一致)刚度振型的平方沿层分布。而对其它结构在弹性状态下，不可用(7)式估计结构楼层变形能反应;当且仅当采用对角质量矩阵时，楼层总输入能反应谱式((6)式)可以采用。

[1] 常 磊，叶献国.结构能量反应的振型分解法研究[J].合肥工业大学学报:自然科学版，2010，33(7):1035-1038，1052.

[2] 常 磊，叶献国.结构能量振型分解反应谱法[J].合肥工业大学学报:自然科学版，2010，33(8):1202-1207.

[3] Shen J，Akbas B.Seism ic energy dem and in steel moment frames[J].Journalof Earthquake Engineering，1999，3(4): 519-559.

[4] Chang Lei，Ye Xianguo，Li Kangning.Analysis of seism ic energy response and distribu tion of RC frame stru ctures [C/CD]//The 14th Word Conferen ce on Earthquake Engineering，Beijing，China，2008:Paper ID14-0224.Beijing: China Earthquake Adm inistration，2008.

[5] 常 磊，叶献国，李康宁.高层混凝土基础隔震结构的损伤与耗能评价[J].土木工程学报，2010，34(9):22-31.

[6] 常 磊.楼层能量的概念及其不平衡原理[EB/OL].[2010-02-24].h ttp://www.paper.edu.cn/paper.php?serialnumber=200912-722.

[7] 常 磊，叶献国，蒋 庆.弹性楼层能量反应的振型非耦合简化表达[J].合肥工业大学学报:自然科学版，2010，33 (10):1527-1530.

[8] 盛宏玉.结构动力学[M].合肥:合肥工业大学出版社，2005:77-78.

[9] 周 云，乐 登，邓雪松.设计用地震动总输入能量谱研究[J].工程抗震与加固改造，2008，30(5):1-7.