基于群结构的可验证视觉密码
2011-03-15卢锦元
卢锦元, 郁 滨
(信息工程大学电子技术学院,河南郑州 450004)
秘密共享是当前密码技术研究的一个重点和热点,它为密钥的管理和保护提供了一种安全的手段,广泛地应用于密钥分发、存取控制、安全多方计算等方面。最早的(k,n)门限秘密共享方案由文献[1,2]分别独立地提出。视觉密码(visual cryptography)作为一种新的秘密共享技术由文献[3]提出,凭借其安全、解密简单的特点,引起了广大学者的研究兴趣。文献[4]将视觉密码方案扩展到通用存取结构,把参与者分为授权子集和禁止子集2个集合,使得秘密信息的分享适用于任意参与者组合,大大拓展了其应用范围。此后,视觉密码的研究主要围绕参数优化[5,6]、彩色图像[7,8]及多秘密分享[9,10]等方面展开。
与其它秘密共享技术一样,视觉密码中也存在着欺骗问题。其欺骗行为,按欺骗者身份划分,有内部欺骗和外部欺骗2种;按欺骗者人数划分,则有单独欺骗和共谋欺骗2种。文献[11]提出了2种信息验证的方案,用来检测恢复图像是否受到非法篡改,但只适用于(2,2)门限结构。对于(k,n)结构,可通过结合(k,n)和(k-1,n)视觉密码方案,来构造防欺骗方案[12],该方案能够检测出k个参与者中的一个欺骗者,但其缺陷在于恢复秘密图像时,存在验证图像的重影。文献[13]对其进行了改进,通过结合原始(k,n)和改进的(k-1,k-1)视觉密码方案,构造了一种更为简单、消除了验证图像的重影、可以清晰地恢复秘密信息的可防欺骗方案,但是没有考虑多个欺骗者合作的共谋欺骗情况。
针对共谋欺骗行为,文献[14]提出了2种方案。第1种通过增加验证份来实现各参与者之间的互相检验,但是每个参与者除了需要保管自己的共享份外,还得另外保管一个验证份,增加了参与者的负担;第2种方案利用(2,n+l)方案来代替(2,n)方案,使得共谋欺骗者推测其它共享份结构的难度增大,但是该方案要求秘密图像由2个互补部分组成,否则无法抵抗特殊欺骗,例如用欺骗图像B冒充秘密图像P。文献[15]构造了一种基于非强存取结构的(k′,k,n)可防欺骗视觉密码方案,该方案能抵抗少于k′人的共谋欺骗,对更多欺骗者的共谋则无能为力。
另外,由于以上方案都是参与者之间互相检测,随着参与者人数的增多,必然导致方案操作的复杂,因此文献[16]提出了一种基于可信第3方的可验证视觉密码方案,其中可信第3方只负责检验参与者的真伪,不参加秘密图像的恢复,从而简化了方案的操作过程。同时,通过对每个共享份进行真实性检验,能够有效防止共谋欺骗。但该方案仍存在2点不足:①与以往大多数视觉密码方案一样,利用代数结构为半群的“或”操作来恢复图像,造成相对差较小,且白像素始终无法完全恢复;②采用将秘密矩阵和验证矩阵并置的方式构造基础矩阵,导致像素扩展度增大,恢复效果不佳。为改善恢复效果,可改变视觉密码的代数结构,用“异或”代替“或”操作,突破半群结构,设计基于异或的视觉密码[17]。文献[18]利用反转操作对其进行了实现,设计了相对差趋于理想的方案,该方案在假设存在一个黑像素完全恢复(k,n)方案的条件下,进行多轮(k,n)方案共享份生成操作,最终,每个参与者获得与操作轮数相等数量的共享份,在解密过程中引入反转操作实现秘密图像的恢复。文献[19]对其进行了改进,通过改变共享份的生成方式,能够在有限轮的操作下,实现完全理想的相对差,但仍然存在着各参与者保存共享份数目过多的不足。
综上所述,本文提出了一种基于群结构的可验证视觉密码方案。方案在分享秘密图像时,通过改变共享份生成方式,实现了像素不扩展;在分享验证图像时,通过引入代数结构为群的异或操作,实现了验证图像的无失真恢复。实验结果表明,本方案的图像恢复效果较以前方案有很大改善。
1 方案设计
首先给出方案定义,其次,结合定义设计方案分享及恢复流程,最后,对方案的有效性进行证明。
1.1 方案定义
不失一般性,设参与者集合为P={P1,P2,…,Pn},可信第3方为Pn+1;秘密图像S的存取结构为(),其中l={Pi1,Pi2,…,Pik};基础矩阵为C0、C1;生成的共享份为Si(i=1,2,…,n)。第3方拥有与S大小相等的n张验证图像Vi,生成的验证份为 Ti。记V(X,M)表示矩阵M中X的分量所在行相“或”得到的行向量,H(V)表示V的汉明重量。
(3)参与者Pi与验证方Pn+1可恢复Vi,形式化描述为Vi=Si⊕Ti,其中,“⊕”表示异或操作。
(4)各参与者及其组合不可恢复Vi,形式化描述为Sj(j=1,2,…,n)与Vi相互独立。
其中,条件(1)、(3)为对比性条件,保证了恢复图像和验证图像的合法恢复;条件(2)、(4)为安全性条件。条件(2)保证了中参与者得不到秘密图像的任何信息;条件(4)则保证了在第3方不到场的情况下,无法进行验证图像的恢复。
1.2 方案流程
该方案中,对于秘密图像采用普通视觉密码方案来分享,例如(k,n)方案,但共享份生成方式有所不同,原方案中是以整个基础矩阵为单位来对像素进行分享的,本方案则以基础矩阵的一列为单位,一个像素对应一列,不存在像素扩展;验证图像的分享利用异或操作来完成。
1.2.1 分享流程
对于秘密图像,分享流程如图1所示,具体步骤如下:
(1)根据秘密图像S中像素点取值c,选择对应的基础矩阵C c,将其进行随机列交换后得到n×m维矩阵M。
(2)随机选取M中某一列M j(j=1,2,…,m),如果该列的第i(i=1,2,…,n)个元素Mj[i]为0/1,则第i个共享份对应位置的像素点颜色为白/黑色。
(3)对原图像中各像素点逐一重复步骤(1)、(2)直至所有像素点处理完。
(4)输出共享份Si。
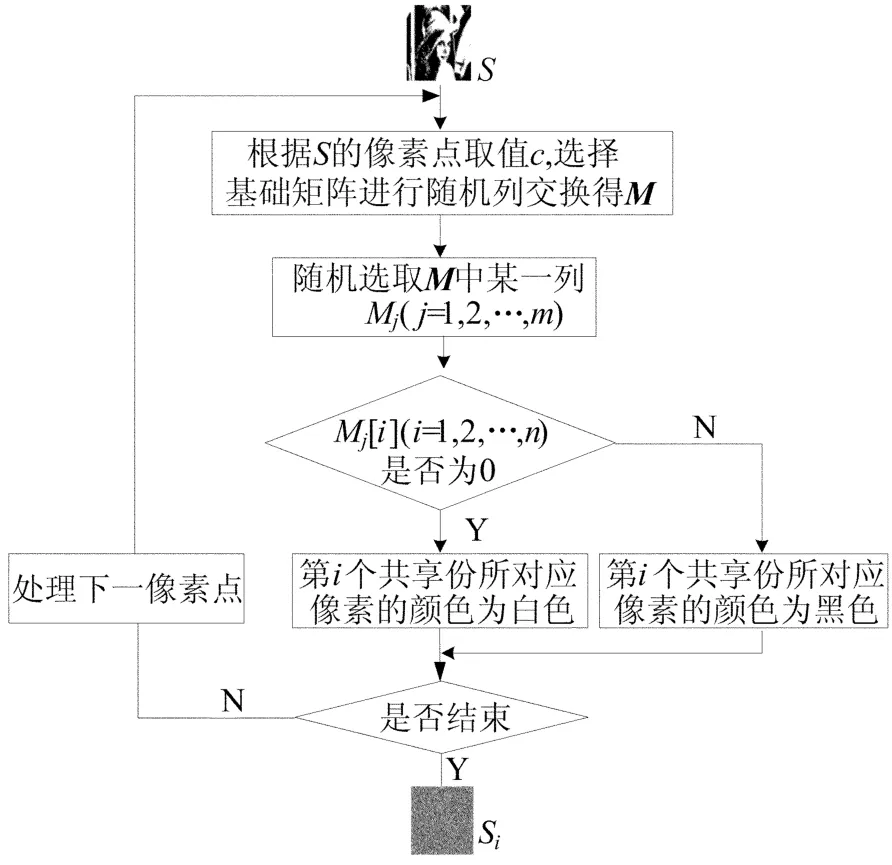
图1 秘密图像分享流程图
分享验证图像时,将各参与者的共享份Si与其验证图像Vi相异或,生成验证份Ti,即Ti= Si⊕Vi(i=1,2,…,n),分享流程图如图2所示。

图2 验证图像分享流程图
1.2.2 恢复流程
(1)秘密图像恢复。将授权集中的共享份叠加即可,即S=Si1+Si2+…+Sik,其中,“+”表示或操作。
(2)验证图像恢复。将共享份Si与其验证份Ti相异或即可,即Vi=Si⊕Ti(i=1,2,…,n)。
1.3 有效性证明
(1)满足定义证明。首先,方案中秘密图像的分享采用的是普通视觉密码方案,如(k,n)-VCS,满足定义第(1)、(2)条;其次,方案利用验证份和共享份相异或来恢复验证图像,满足定义第(3)条;最后,各参与者拥有的共享份,在分享验证图像之前已经产生,与验证图像相互独立,从参与者所持有的共享份中得不到验证图像的任何信息,满足定义第(4)条。
(2)完全恢复证明。验证图像的分享和恢复均由异或操作来完成,而异或运算在二值域上是群结构,其中的每个元素都存在逆元,它使验证图像的分享及恢复过程互逆。分享过程中,当Vi为白时Si和Ti中对应像素点取值相等,否则相反。在验证时,通过将Si和Ti相异或来恢复验证图像,而异或操作中,两分量相同时,恢复全白,反之则恢复全黑,因此,黑白像素得以完全恢复。
2 实验与分析
2.1 实验结果
不妨设参与者集合P={P1,P2,P3,P4},验证方为P5,秘密图像S的存取结构为(2,4)门限结构,其基础矩阵为:


图3 秘密图像及验证图像

图4 各共享份及验证份

图5 恢复效果对比图
从图5可以看出,与以往方案相比,本文方案恢复效果有很大改善。各共享份与原图像大小相等,不存在像素扩展,而且验证图像实现了无失真恢复。
2.2 实验分析
对于视觉密码而言,像素扩展度和相对差是2个重要的参数,可以用来评价方案的优劣。表1是本文方案与文献[16]方案的一个参数对比。其中,m、h、l分别为(ΓSQual,ΓSForb)-VCS中像素扩展度、黑像素的黑度、白像素的黑度;n为参与者人数。

表1 本文方案与文献[16]方案参数对比
由表1可知,本文方案在2个参数上都有显著改善,特别是验证图像的2个参数均为最优值。
3 结束语
本文提出了一种基于群结构的可验证视觉密码方案,该方案以基础矩阵的列为单位对秘密图像的像素进行分享,同时,通过代数结构为群的异或操作,将验证图像的分享及恢复过程设计成互逆。仿真实验表明,本方案具有像素不扩展、验证图像无失真恢复的特点。
本文初稿首次刊登于《计算机技术与应用进展◦2010》
[1] Sham ir A.H ow to share a secret[J].Comm unicationsof the ACM,1979,22(11):612-613.
[2] Blakley G R.Safeguarding cryptographic keys[C]//Proc A FIPS,1979:313-317.
[3] Naor M,Shamir A.Visual cryptog raphy[J].Lectu re Notes in Compu ter Science:Advances in Cryptology-Eu rocrypt' 94,1995,950:1-12.
[4] A teniese G,Carlo B,Santis A D,et al.V isual cryptography for generalaccess structures[J].Information and Computation,1996,(12):86-106.
[5] Blundo C,De Santis A,Stinson D R.On the con trast in visual cryptog raphy schem es[J].Journal of Cryptography,1999,12(4):261-289.
[6] Fang Liguo,Yu Bin.Research on pixel expansion of(2,n) visual th reshold scheme[C]//1st International Symposium on Pervasive Compu ting and Applications P roceedings(SPCA 06),Ningbo,China,2006:856-860.
[7] Cimato S,De Prisco R,De Santis A.Optimal colored th reshold visual cryp tography schemes[J].Designs,Codes and C ry ptog raphy,2005,35(3):311-335.
[8] Ng F Y,W ong DS.On the security ofa visual cryptography scheme for color images[J].Pattern Recognition,2009,42 (5):929-940.
[9] Yu B,Fu Z X,Fang L G.A modified mu lti-secret sharing visual cryptography scheme[C]//In ternational Conference on Compu tational Intelligence and Security,2008: 351-354.
[10] Fu Z X,Yu B.Research on rotation visual cryptography scheme[C]//2009 In ternational Symposium on Information Engineering and Electronic Commerce,Ternopil,U-kraine,2009:533-536.
[11] 陈玲慧.视觉化密码之研究及其应用[R].台北:台湾行政院科学委员会,1999.
[12] 郭 洁,颜 浩,刘 妍,等.一种可防止欺骗的可视密码分享方案[J].计算机工程,2005,31(6):126-128.
[13] 徐晓辉,郁 滨.无重影的可防欺骗视觉密码方案[C]//计算机技术与应用进展(CICAS2007),2007:1335-1339.
[14] Gw oboa H,Tzungher C,Dushiau T.Cheating in visual cryp tography[J].Designs,Codesand Cryptography,2006,38:219-236.
[15] 王益伟,郁 滨.一种(k′,k,n)可防欺骗视觉密码方案[C]//全国第 19届计算机技术与应用学术会议(CACIS08),2008:492-496.
[16] Yu B,Fang L G,Xu X H.A verifiab le visual cryptography scheme[C]//CIS2008,Suzhou,China,2008:347-350.
[17] TuylsP,H ollmann H D L,Vanlin t J H,et al.XOR-based visual cryptography schemes[J].Designs,Codes and Cryptography,2005,37:169-186.
[18] V iet D Q,Ku rosaw a K.A lmost ideal contrast visual cry ptog raphy w ith reversing[J].Lectu re Notes in Computer Science,2004,2964:353-365.
[19] Cimato S A,Santis D,Ferrara A L,et al.Idealcon trastvisual cryptog raphy schem es w ith reversing[J].Information Process Letters,2005,93(4):199-206.
