FCM属性约简方法在汽轮机故障诊断中的应用

齐晓轩， 纪建伟， 原忠虎

(1.沈阳农业大学信息与电气工程学院，辽宁沈阳 110161;2.沈阳大学信息工程学院，辽宁沈阳 110044)

0 引 言

故障诊断具有复杂性、多样性、不确定性等特点[1]。为了提高故障诊断的可靠性，需要获取大量的故障征兆参数来全面描述故障模式。故障诊断过程中，不同征兆参数的重要性有所不同，有些参数甚至是冗余的。另外，在参数信息获取过程中，通信异常也可能导致故障信息的不一致或不完备。如果不加选择地将全部参数信息直接用于诊断，必然会降低故障诊断的准确性和实时性，因此，对故障诊断中的冗余征兆参数进行约简是十分必要的。

粗糙集是波兰学者Pwalak于1982年提出来的一种数学工具[2]，能有效地分析不精确、不一致和不完整等不完备信息，从中发现隐含知识，揭示潜在的规律。基于粗糙集的属性约简方法被广泛应用于特征选择过程中，可以在保证分辨能力的前提下，对输入征兆信息进行约简，降低特征向量的维数[3]。文献[4]提出了一种基于变相似度的模糊粗糙集模型，在保证分类准确性的前提下获得多层次的属性约简集合，以增强对信息的灵活掌握;文献[5]运用差别矩阵元素项的特性，提出了一种新的启发式约简完备算法，可有效地降低区分矩阵约简算法的空间复杂度;文献[6]提出了一种基于概念格模型的完备约简算法，解决了区分矩阵算法的局限性以及启发式算法的不完备性等问题;文献[7]提出了一种基于核值信息和吸收率的优化算法，对分辨矩阵的构造过程进行了改进，简化运算，提高了时间性能。

经典的粗糙集理论只能处理离散化数据，在属性约简之前须对连续属性进行离散化处理，以减少属性值的数目，降低问题的复杂性、提高知识的适应度。离散化处理的原则是:保持信息系统中所表达的样本分辨关系，避免信息丢失或错误。常用的离散化方法有:经验分割法、等频法、等距法、NaveScaler算法、贪心算法以及粗糙集与布尔逻辑结合法等，这些方法均有着各自的适用性，但同时也有其局限性。文献[8]采用等距法对条件属性进行离散化处理，缺点是需要预先设定分割的区间数，而合适的区间数通常需要经过反复实验或凭借领域专家经验才能找到，适应性较差;文献[9]采用监督式局部离散化方法，使得每个条件属性都对决策规则产生作用，实际应用结果表明，其识别准确率要高于全局离散化方法，但由于其计算量较大，导致数据处理的实时性较差。

由于粗糙集理论对原始数据本身的模糊性和不确定性缺乏相应的处理能力，与模糊数学和概率论等结合，则可在一定程度上减少由于离散化造成的信息损失问题。本文将模糊集引入到粗糙集理论中，利用模糊c均值聚类算法(FCM)对故障征兆参数空间进行划分，实现属性值的离散化处理，利用粗糙集理论实现属性约简，基于支持向量机(SVM)建立故障诊断模型，并应用于汽轮机故障诊断系统中。

1 基于FCM的粗糙集故障特征选择

1.1 粗糙集基本概念

定义1 知识表达系统和决策表。粗糙集理论将故障诊断样本数据描述为一个知识表达系统S，S可以表示为:

其中，U为论域，表示诊断对象;C∪D=R为属性集合;子集C为条件属性集，表示故障样本的特征集合，对应特征向量矩阵T;子集D为决策属性集，表示各故障样本对应的故障类型;V为属性值集;f:U×R→V，是一个信息函数，指定U中每一个对象的属性值。具有条件属性和决策属性的知识表达系统就是决策表。决策表为一张二维表格，表中每一行描述一个故障样本，每一列表征样本的一种故障特征属性。

定义2 决策属性D对条件属性C的依赖度定义为:

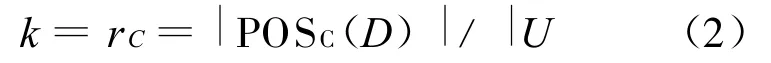
依赖度k表示在条件属性C下能够确切划入决策类U/D的对象与U上全体元素数目的比率，表达了决策属性对条件属性的依赖程度，显然，0≤k≤1。

定义3 任意属性a∈(C-R)关于决策属性D的重要性定义为:

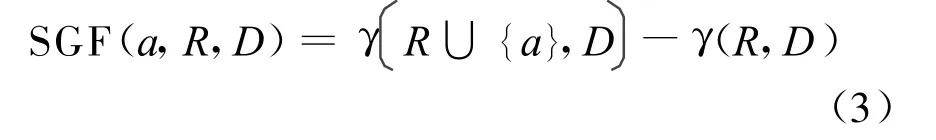
对于属性a∈C，如果γ(C，D)=γ(C-a，D)，则称属性a相对于决策属性D是冗余的，否则是不可缺少的。如果C中的任意属性相对于D都是不可缺少的，那么C相对于D是独立的。

1.2 基于FCM算法的属性约简

1.2.1 离散化问题描述

已知目标信息系统S=(U，C，D，V，f)，C∪D=R为属性集合，论域U={x1，x2，…，xn}。设决策类别个数为r(d)。属性a的值域Va上的一个断点可记为(a，c)，其中，a∈R，C为实数集。在值域Va=[la，ra]上的任意一个断点集合{(a，}定义了Va上的一个分类Pa，即

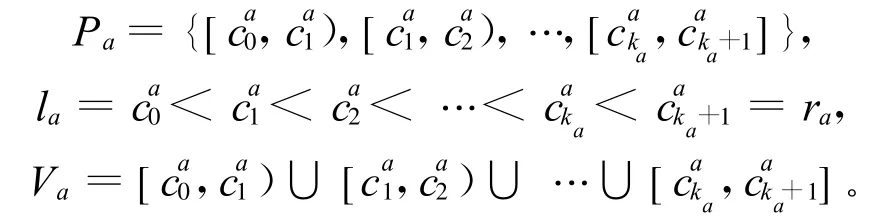
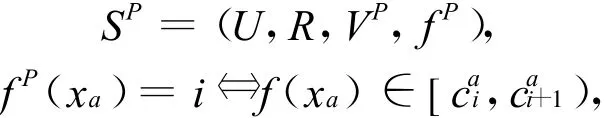
对于x∈U，i∈{0，1，…，Ka}。离散化过程就是将相邻断点间的属性值进行合并的过程，通过合并属性值来减少问题的复杂度。

经过离散化后，从原有的决策系统中产生了新的决策系统，而不同的断点集合又会构造不同的决策系统，显然，离散化的过程伴随着信息的丢失。

1.2.2 模糊c均值聚类分析

模糊聚类的基本思想是:在分类条件给定的情况下，利用FCM算法寻找出对事物的最佳分类方案。将有限样本集 X={x1，x2，x3，x4，…，xn}分为C类，各样本以一定的程度隶属于C个不同的类域。用μij表示第j个样本隶属于第i类的隶属度，μij满足如下3个约束条件[10]:

则分类结果可以用一个c×n阶矩阵U来表示，称为模糊矩阵。模糊c均值聚类算法的出发点是基于对目标函数的优化，对平方误差函数(4)式求最优值，即

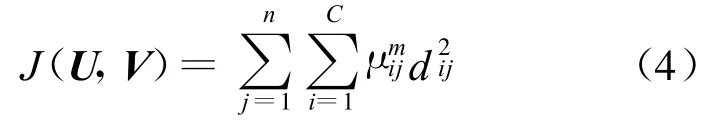
其中，C为聚类中心个数;m为加权指数，m∈[1，∞];dij=‖xj-vi‖为样本到中心矢量的距离;xj为第j个样本。

J(U，V)代表了各样本到聚类中心的加权距离平方和，权重是样本xi对第i类隶属度的m次方，若m=1，则退化为硬c均值算法(HCM);若m＞1，可用最小二乘法找出一个恰当的模糊c组分类矩阵U和恰当的聚类中心V，使得J(U，V)达到最小。问题可以归结为在约束条件(2)下的条件极值问题，用Lagrange乘子法使J(U，V)取极小值。

1.2.3 决策表的约简

在获得离散化后的决策表后，可以对其实施有效的约简。属性约简是指在保持系统分类或决策能力不变的情况下，删除其中不重要和冗余的属性。

定义4 设C和D分别是决策表的条件属性集合和决策属性集合，对于C的子集C′，若满足:

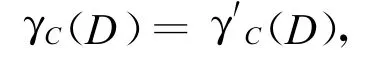
从C′中删除任何属性a后都有γ′C-{a}(D)= γ′C(D)，则称C′是C相对于决策属性D的一个约简。

一个决策表可能同时存在几个约简，这些约简的交集定义为决策表的核core(R)。在故障诊断应用中，往往并不需要计算出知识表达系统中的所有约简，而是结合领域特点，选择用户感兴趣的或经济可行的约简集。

2 故障诊断实例

2.1 汽轮机故障诊断

由于设备结构的复杂性和运行环境的特殊性，汽轮机的故障率较高，故障危害性也很大。如何及时、准确地诊断汽轮机设备故障，减少或避免事故的发生，已经受到国内外学者的普遍关注。汽轮机振动是影响安全运行的一个重要指标，当设备运行异常时，通常会出现振动增大、振动性质改变等现象[11]，通过对振动信号的分析，可以在不停机的情况下对故障进行有效诊断，满足实际生产需求。

汽轮机常见的振动故障有不平衡、不对中、油膜振荡、喘振、磨碰、轴承损害及松动等故障，可以把汽轮机故障诊断看做一个模式分类问题，每一类故障对应一组特征集。以汽轮机振动信号频谱特征中(0.01～0.39)f、(0.40～0.49)f、0.50 f、(0.51～0.99)f、1 f、2 f、(3～5)f、odd×f、＞5 f (f为工频，odd×f为奇数倍f)9个不同频段上的谱峰能量值作为故障征兆属性，得到故障特征向量X={x1，x2，x3，x4，…，x9}，对N个故障样本进行分析，形成初始特征向量矩阵T，即

无论从计算的复杂度还是分类器的性能来看都不适宜直接对T进行处理，因此需要进行进一步的特征选择;同时，鉴于故障信息的模糊性和不确定性，本文采用FCM聚类算法分析汽轮机的振动故障原因，实现对故障征兆空间的划分，然后利用粗糙集理论对故障特征向量进行约简。

2.2 实验结果

本文利用模糊粗糙集在故障诊断之前对样本进行预处理，保留关键信息，去掉冗余属性，剔除相同样本，简化SVM故障分类器的训练难度，在保证分类精度的前提下，提高系统诊断的实时性，诊断模型如图1所示。

每一条汽轮机故障样本定义为论域U中的一个对象。每个故障特征信息定义为条件属性C的一个元素，而各种故障类型则定义为决策属性D的一个元素。根据以上定义对文献[11]中的汽轮机故障数据进行分析，并对故障样本各频段的频谱特征向量做归一化处理，得到一个信息表。随机选取12条数据作为训练样本集，见表1所列，其余的用作测试样本集。汽轮机故障说明见表2所列。

采用FCM对连续属性数据进行离散，建立知识表达系统。在聚类过程中，聚类数目的确定很关键，数目过少会导致不兼容信息的产生，聚类数目过多则会由于过度离散化而导致决策表复杂化，文献[12]对所有的条件属性采用统一的断点指导方法，未考虑条件属性个体之间的差异，本文所提出的方法充分考虑各连续属性的特点，通过对样本集9个条件属性做出的空间分布状态图确定属性值的离散区间取值，因而对于故障信息的挖掘更充分，进而获得反映故障征兆本质的约简属性集，提高诊断的准确性。离散化结果，见表3所列。

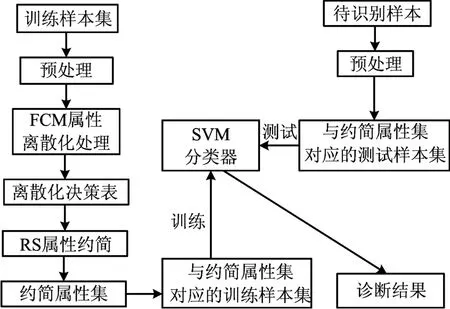
图1 故障诊断模型

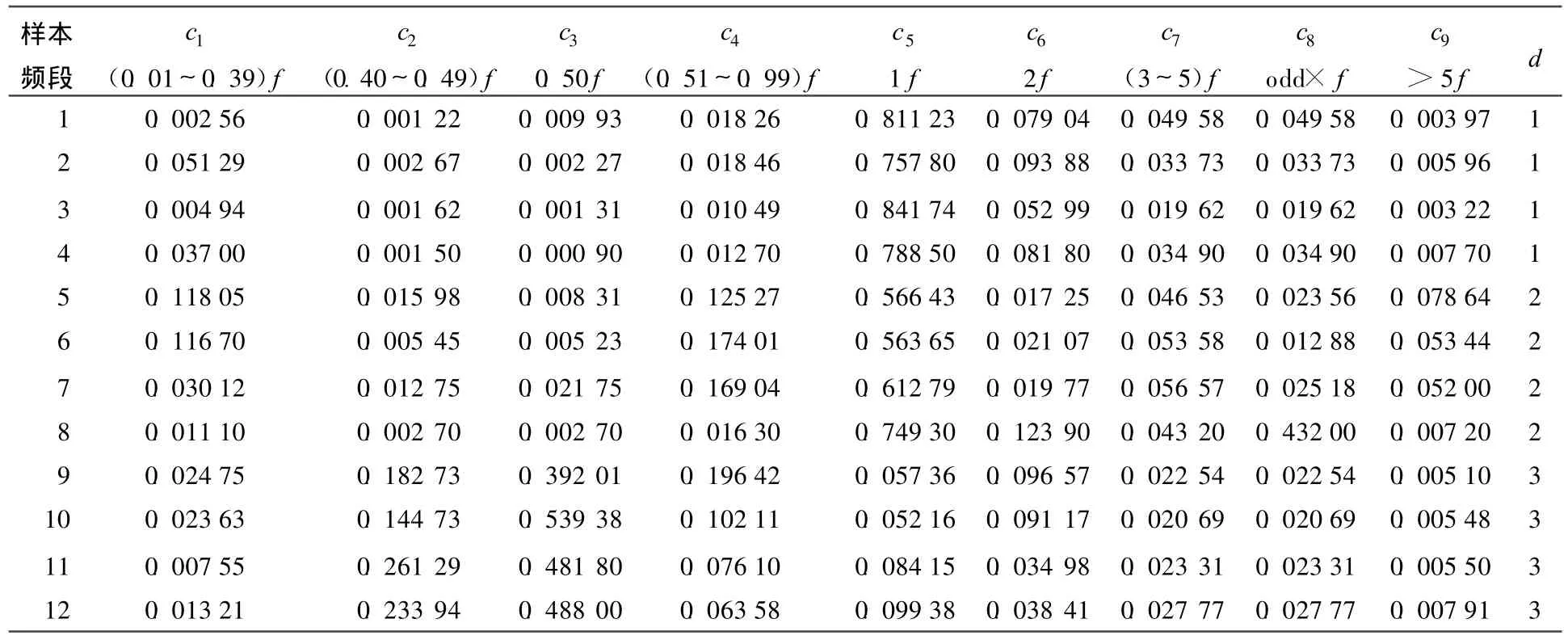
表1 汽轮机故障训练样本集

表2 汽轮机故障说明

对表3所列信息系统进行属性约简后得到约简属性集{c1，c4，c8}，根据所得到的约简属性集和对应的原始数据，形成新的样本集，实现基于SVM的故障分类器的训练和测试。在实验过程中，SVM分类器选用径向基核函数K(x，xT)= exp(-γ‖xi-xj‖2)，参数γ取值为10，采用交叉验证的方法。通过对测试样本的诊断实验，识别率可达100%。用约简属性集训练的系统与用全部属性训练的系统相比，在保证了识别率的同时，降低了系统计算的复杂程度，从而可以提高诊断的实时性能。

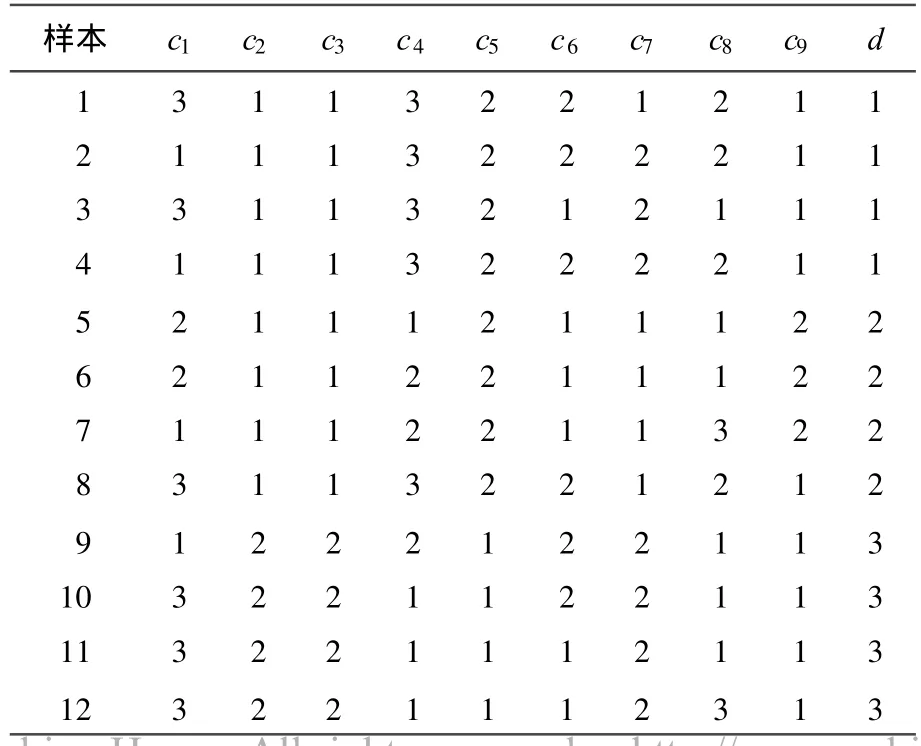
表3 属性离散化之后的决策表

3 结束语

本文基于FCM聚类算法对故障征兆参数空间进行划分，利用粗糙集理论进行属性约简，基于SVM建立分类器，实现汽轮机系统的故障诊断。采用本文所提出的方法，可以有效解决征兆属性离散化过程中存在的信息损失问题，降低SVM训练难度并避免其应用中的“维数灾难”问题，克服SVM在故障诊断中的局限性，提高汽轮机故障诊断的准确性和实时性，降低故障诊断成本。

本文初稿首次刊登于《计算机技术与应用进展◦2010》

[1] 陈长征，刘 强.概率因果网络在汽轮机故障诊断中的应用[J].中国电机工程学报，2001，21(3):78-81.

[2] Paw lak Z.Rough set[J].International Jou rnal of Computer and Information Sciences，1982，(11):341-356.

[3] Dǜntsch I，Gediga G.Roughian:rough information analysis [J].International Jou rnal of Intelligent Sy stem s，2001，16 (1):121-147.

[4] 张慧哲，王 坚，梅宏标.一种变相似度的模糊粗糙集属性约简[J].模式识别与人工智能，2009，22(6):393-399.

[5] 王加阳，高 灿.改进的基于差别矩阵的属性约简算法[J].计算机工程，2009，35(2):66-67，73.

[6] 胡学钢，薛 峰，张玉红，等.基于概念格的决策表属性约简方法[J].模式识别与人工智能，2009，22(8):624-629.

[7] 史君华，胡学钢.一种基于粗集的决策表属性值约简改进算法[J].合肥工业大学学报:自然科学版，2008，31(1): 36-39.

[8] 梁武科，赵道利，马 薇，等.基于粗糙集-RBF神经网络的水电机组故障诊断[J].仪器仪表学报，2007，28(10): 1806-1810.

[9] 关 欣，衣 晓，何 友.一种新的粗糙集属性约简方法及其应用[J].控制与决策，2009，24(3):464-467.

[10] 王启志，王晓霞.模糊聚类在机械故障诊断中的应用[J].轴承，2008，(10):35-38.

[11] 何 青，杜冬梅，李 红.汽轮发电机组远程智能故障诊断系统[J].热能动力工程，2006，21(5):532-536.

[12] 李 鹏.基于粗糙集和支持向量机的汽轮机振动故障诊断研究[D].保定:华北电力大学自动化系，2008.