应用于毫米波反射计的多项式校准方法
2011-03-15刘金扬苗俊刚
赵 鑫 刘金扬 苗俊刚
(北京航空航天大学 电子信息工程学院,北京 100191)
姜景山
(中国科学院 空间科学与应用研究中心,北京 100190)
应用于毫米波反射计的多项式校准方法
赵 鑫 刘金扬 苗俊刚
(北京航空航天大学 电子信息工程学院,北京 100191)
姜景山
(中国科学院 空间科学与应用研究中心,北京 100190)
为了在毫米波波段准确测量波导器件的反射系数,提出了一种应用在反射系数测试前端(反射计)中的校准方法.该校准方法采用基于多项式的误差模型,使得每一个误差项的求解都转化成一个求解轨迹圆圆心的问题,同时不影响求解精度.采用一个滑动负载、一个滑动短路和一个短路器,在毫米波波段降低了对标准件理想程度的要求.实验中搭建了一个Ka波段的反射计,图解误差项的求解过程,分析了误差项的物理意义.把校准后的测量结果与商用矢量网络分析仪(VNA,Vector Network Analyzer)进行比较,吻合较好.同样比较了一组W波段反射计对波纹喇叭的测量结果,进一步验证了方法的合理性.
毫米波;反射系数;反射计;校准;标准件;多项式
毫米波和亚毫米波波段,散射参量的测量能力成为制约该波段器件发展的重要因素.反射计用于反射系数的测量,直接的测量结果是存在误差的,这来源于硬件的不理想.如果对硬件建立误差模型,通过一系列标准件的测量来求解误差,真实结果就可以由软件对测量结果修正得到,这一过程就是校准.由于商用反射计采用很高的硬件指标,配合较为理想的标准件,可以使用 TRL(Through-Reflect-Load)或OSL(Open-Short-Load)校准方法[1-3].虽然 TRL方法操作简单精度也很高,但需要利用双端口校准,在毫米波波段常用的单端口测量中不实用[4].OSL方法是反射系数测量中常用的方法,它采用一个匹配负载,一个短路器,以及一个偏置短路器.其中,波导接口的偏置短路器采用偏置距离为波导波长1/4的短路器以形成开路状态.在毫米波波段,偏置距离的偏差对实际相位的影响变大.例如在频率100 GHz时,WR-10波导中的波导波长约4mm,那么偏置距离0.1mm的偏差将给测量相位造成18°的误差.文献[4-6]中使用滑动短路代替偏置短路器,由于无需确知滑动短路的实际位移,所以避免了位移偏差带来的误差.在实际的反射计系统设计中,特别是在毫米波波段,标准件难以接近理想.于是适合毫米波反射计的校准方法需要采用滑动终端,从而降低对标准件理想程度的要求.
传统的误差模型是基于分式的,如果变换到多项式上,则便于使用滑动终端的求解,而不影响求解精度.本方法用一个滑动负载和一个滑动短路逐个求解误差项,用一个短路器建立相位参考面.滑动负载的终端反射系数不用预知,滑动短路的终端反射系数作为标准的单位量,短路器的结构也相当简单,所以该方法采用了容易实现的标准件,也能获得较高精度,满足实验室的应用.
本文首先建立反射计的误差模型,推导出基于多项式的误差项表达式,由此给出校准步骤;以Ka波段的反射计为例,对误差项的求解过程进行图解说明,分析了误差项量值的物理意义;最后分别在Ka波段和W波段与矢量网络分析仪(VNA,Vector Network Analyzer)的测量结果进行比较.
1 理论模型
在微波测量中,待测物(DUT,Device Under Test)的反射系数无法直接获取.一般通过搭建微波网络,间接获取测试端口处的入射和反射信号,从而得到反射系数.典型的单端口反射计原理图如图1所示,包括信号源、隔离器、2个定向耦合器以及衰减器.

图1 反射计原理图
反射计在结构上可视作图2a中的4端口网络(4 端口分别为 t1,g2,a,b),用 bi,ai分别表示第i个端口的出射和入射信号,用S表示该4端口网络的散射参量,有如下关系:


图2 反射计中的误差模型
注意到,测量结果ΓM=b4/b3,实际结果Γ=a2/b2,文献[7]推导出它们之间满足双线性变换的关系表达式:

其中,A,B,C是系统常数.这个变量关系由图2b描述,那么ΓM是由Γ通过一个2端口矩阵E变换得到.下面通过分析图1中接收端b,a的信号组成,可以明确由Γ变换到ΓM的物理意义.
设两个耦合器的传输系数为 T1,T2,耦合系数为 C1,C2,隔离系数为 I1,I2,衰减器的传输系数为A,待测端口的反射系数为R.根据一般的器件参数,对应系数见表1.

表1 毫米波器件的参数(线性值)
在图1中,t1,g1分别为DC1两端的入射和反射信号,t2,g2分别为DC2两端的入射和反射信号,Γ为DUT的反射系数.先假设除DUT之外的其它器件无反射,t1为入射信号,可以得到

于是b,a两路的信号组成为



通过级数展开,得到多项式的形式:

于是b路信号除以a路信号,消除入射信号t1影响,得到
跟据Γ的精确度指标(待测Γ在1到0.001范围内,要求幅度误差小于0.1 dB(2%)),下面来判断多项式截取至二次项时能否达标.在式(6)中将Γ视为真值Γ0,以表1中数据为参考,方程如下:
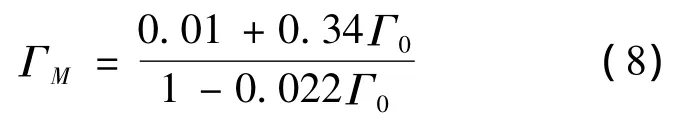
对式(7)中多项式截取至二次项,并代入表1中数据,方程为

当待测Γ在1到0.001之间变化时,由式(9)求解得到的Γ存在相对误差:
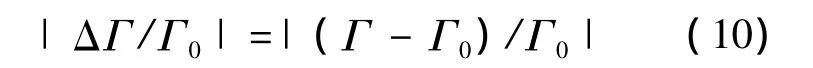
即便考虑到极差的硬件参数(按照R=0.01,0.03,0.1 分为极优、正常、极差的情况),图 3 中给出了相对误差随Γ的变化始终不超过0.6%,正常情况下也不超过0.1%.以上说明使用截取至二次项的多项式不影响待测Γ的精确度,于是采用表达式:

其中

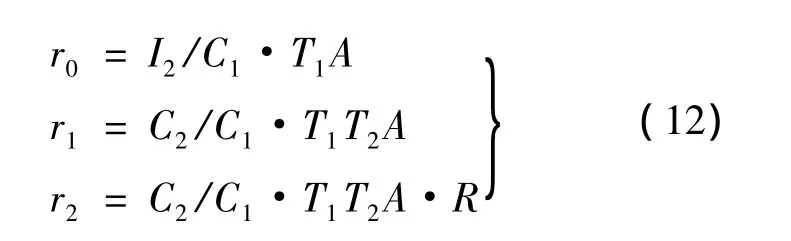
注意到|p1|→0,于是用器件系数表示3个误差项:其中,r0体现出耦合器的定向性;r1体现出主通道的路径系数;r2体现出测量端口的匹配性能.
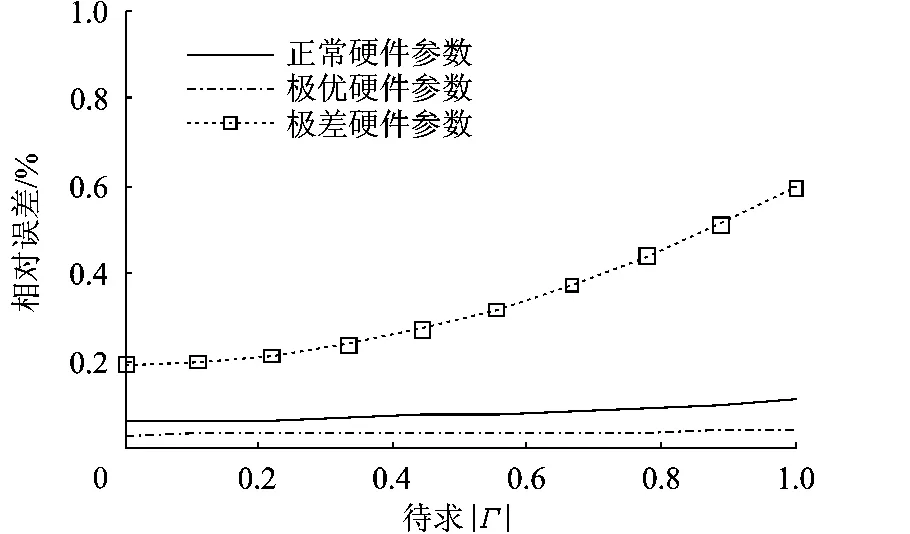
图3 截取至二次项后对求解Γ的影响
2 校准过程
使用滑动终端时,可以获得幅度恒定、相位线形变化的标准件.校准中,由幅度未知的滑动负载,可以求解r0;由幅度作为单位量的滑动短路,可以求解r1,r2;如果需要测定绝对相位,可以由短路片来标定相位参考面.校准过程见图4,具体步骤如下:

图4 校准流程图
1)使用滑动负载时,测量端口处

其中,β表示传输线的波阻抗;k1表示刻度;A1和θ1分别为0刻度时的幅度和相位.
通常有|Γ1|≪1 和|r2|≪1,使得代入式(11)中得到表达式:
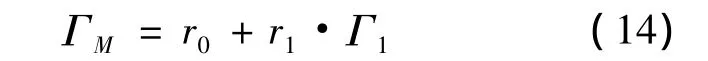
表现为一个圆周.于是采用最小二乘法拟合[8],对测试数据Γ'M的轨迹求圆心,得到r0.
2)使用滑动短路时,测量端口处

其中设定幅度为单位量1,令0刻度时的端口相位为0.
通过对式(11)移项变换,得到表达式:

令 P1=(ΓM-r0)/Γ2,则 P1表现为一个圆周.对测量数据P'1的轨迹求圆心,得到r'1.
通过对式(16)进一步的移项变换,得到表达式

令 P2=[(ΓM-r0)/Γ2-r1]/Γ2,则 P2表现为一个点.对测量数据P'2的轨迹求圆心,得到r'2.
3)使用短路片时,已经得到步骤(2)中标定的r1和r2.由测得Γ'M代入方程(11)可以解出Γ(求解关于Γ的二次方程时,其中一根远大于1,故舍去),得到此时的相位θ3.令短路片反射系数的相位为-180°,由此标定测量端口处的相位参考面,需要对r1和r2作如下修正:

3 实验验证
为验证校准方法,搭建了图5a所示的Ka波段反射计.在安捷伦8530A接收机平台上,通过8倍频毫米波倍频器,频率扩展到26.5~40GHz.倍频器依次连接隔离器ISO,定向耦合器DC1,衰减器ATT,定向耦合器DC2,最后是波导接口输出.测量端口处,待测物DUT的入射和反射信号分别耦合到参考和测试信号,经8次谐波混频器送入接收机.发射端输入功率设为4 dBm.
按照校准流程,分别使用滑动负载、滑动短路,得到测试数据Γ'M,P'1,P'2在极坐标中的圆周轨迹.图6a给出了在频率40GHz时的3个轨迹圆周,其圆心分别对应着的3个误差项.如果对每个频点进行类似处理,可以得到图6b中的误差项频响曲线,该曲线反映出系统特性:|r1|≈0.3(-10 dB)是来自衰减器的10 dB衰减量,|r0|≈0.001(-60 dB)和|r|≈0.002(-45 dB)分别反映出耦合器的方向性为50 dB、测量端口的回波损耗为-35 dB.反射计完成校准后,对一个匹配负载进行测量.修正后的结果与通过商用VNA测量的结果进行比较,如图7a所示.由于实际测量受到法兰盘装配的影响较大,导致两条曲线不够吻合,但都能说明该匹配负载在Ka波段上的回波损耗基本都在-40 dB以下.
按照同样原理搭建的W波段反射计如图5b所示,采用了准光学技术,用准光学器件代替了相应的波导器件.反射计使用该方法校准,测量波纹喇叭的结果见图7b.除去高频段的部分频点,两者的结果能取得较好的一致.

图5 反射计的实验场景

图6 误差项的求解
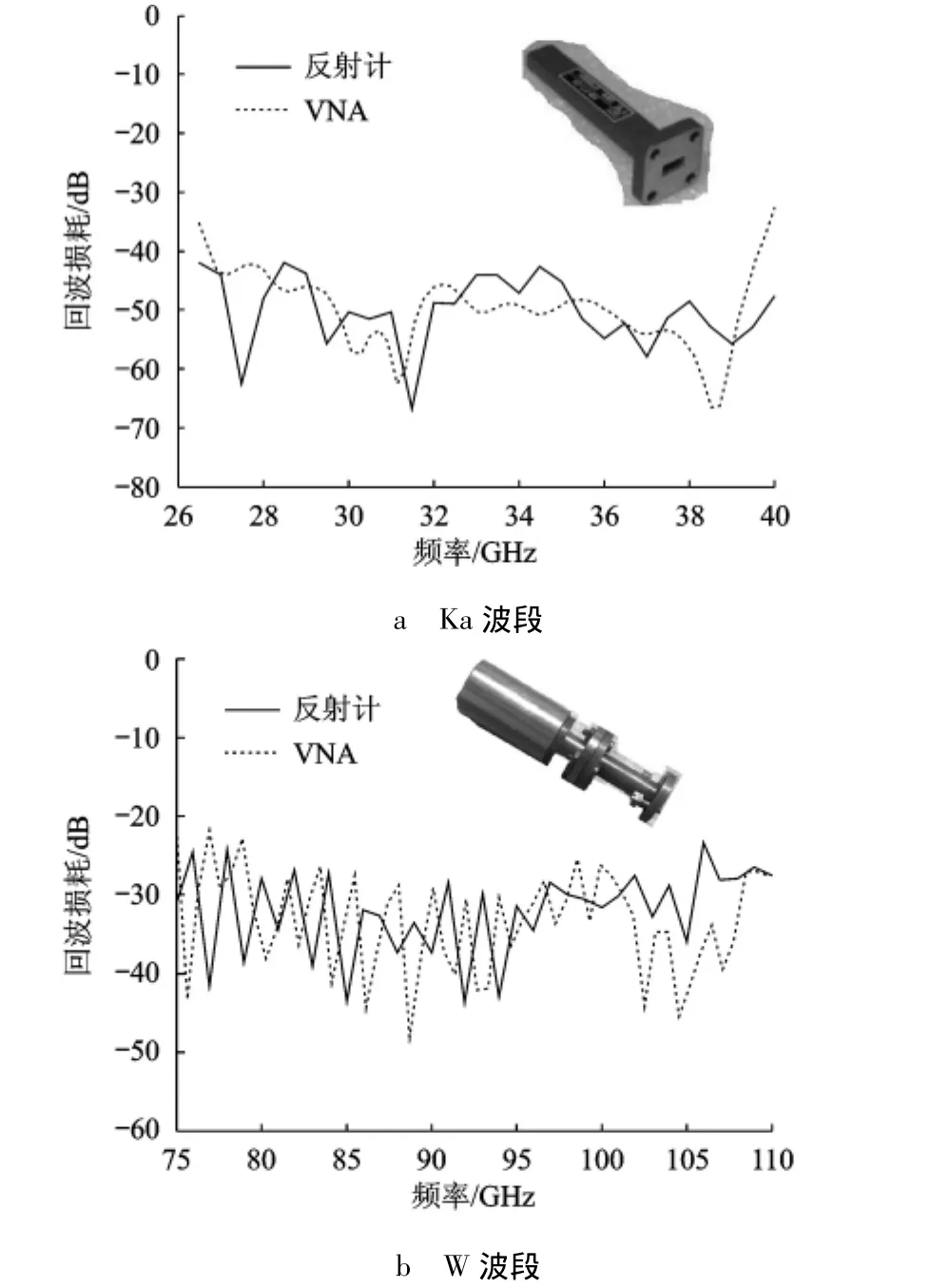
图7 反射计与商用VNA测量结果的比较
4 结 束 语
本文研究了传统的误差模型和校准方程,分析了端口的信号组成,在此基础上提出对传统校准方程的改进.改进后的方程便于使用滑动终端进行求解,而且各个误差项的求解方式相似,有利于软件的模块化.误差项的频响曲线体现出硬件指标,为硬件设计提供了方向.多项式校准方法在Ka波段和W波段取得了较好的测量结果,适合在毫米波波段中的应用.未来计划将该方法推广到更高频段,比如300GHz波段上的反射计.
References)
[1] Agilent Technologies.Agilent PNA microwave network analyzers,application note 1408-15[EB/OL].Santa Clara,CA:Agilent Technologies,Inc,2009[2010-08-01].http://na.tm.agilent.com/pna/files/an1408-13.pdf
[2] Hiebel Michael.Millimeter-wave measurements using converters of the R&S ZVA family,application note 1EZ55[EB/OL].Rohde&Schwarz GmbH&Co KG,2007[2009-11-01].http://www2.rohde-schwarz.com/file/1EZ55_0E.pdf
[3] Fung A,Dawson D,Samoska L,et al.Two-port vector network analyzer measurements in the 218-344-and 356-500-GHz frequency bands[J].IEEE Transactions on Microwave Theory and Techniques,2006,54(12):4507 -4512
[4] Wiatr W,Lewandowski A.Multiple reflect technique for wideb and one-port VNA calibration[C]//International Conference on Microwaves,Radar&Wireless Communications.Krakow:IEEE,2006:37 -40
[5] Wiatr W.A broadband technique for one-port calibration of VNA[C]//International Conference on Microwaves and Radar.Krakow:IEEE,1998:363-367
[6] Sigg W,Simon J.Reflectometer calibration using load,short and offset shorts with unknown phase[J].Electronics Letters,1991,27(18):1650-1651
[7] Oldfield LC,Ide JP,Griffin E J.Amultistate reflectometer[J].IEEE Transactions on Instrumentation and Measurement,1985,34(2):198-201
[8]颜庆津.数值分析[M].3版.北京:北京航空航天大学出版社,2006:135-141 Yan Qingjin.Numerical analysis[M].3rd ed.Beijing:Beijing U-niversity of Aeronautics and Astronautics Press,2006:135 -141(in Chinese)
(编 辑:娄 嘉)
Polynomial calibration method for millimeter-wave reflectometer
Zhao Xin Liu Jinyang Miao Jungang
(School of Electronics and Information Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Jiang Jingshan
(Center for Space Science and Applied Research,Chinese Academy of Sciences,Beijing 100190,China)
In order to measure the accurate reflection coefficient of waveguide component at mill imeter wave band,a method for reflec to meter calibration was proposed.The calibration method was based on a polynomial error model,making the solution of each error term transformed into a problem solving the center of a circle trace,without reducing the solution precision.The method adopted a sliding load,a sliding short and a short circuit,thus reduced the requirements of standards in the millimeter-wave band.In experiment,a Kaband reflec to meter was built,the errors'solving processes and physical meanings were presented.After calibration,measurement results from reflectometer and vector network analyzer(VNA)were compared,and good agreement was achieved.Measurement results of a W-band corrugated horn were also compared,which further validate the method.
millimeter waves;reflection;reflectometers;calibration;standards;polynomials
TM 934.72
A
1001-5965(2011)06-0728-05
2010-11-25
国家杰出青年科学基金资助项目(40525015)
赵 鑫(1983 -),男,湖北黄梅人,博士生,xinzhao@ee.buaa.edu.cn.
