基于神经网络液体横向晃动时罐体受力的预测

康 宁 贾 嘉 刘献栋

(北京航空航天大学 交通科学与工程学院，北京 100191)

基于神经网络液体横向晃动时罐体受力的预测

康 宁 贾 嘉 刘献栋

(北京航空航天大学 交通科学与工程学院，北京 100191)

用Fluent软件，VOF(Volume of Fluid)模型，对基准罐体在不同充液比下受到横向加速度时的受力进行数值模拟;以充液比、前两时刻基准罐体受力、加速度及将要经历的加速度作为输入，以下一时刻受力作为目标输出，选用合理的计算结果作为训练样本，建立基于BP神经网络液体横向晃动时基准罐体受力的预测模型，用158个样本对完成训练的网络进行可靠性验证，横向力、垂向力和侧倾力矩最大预测误差分别为8.88%，0.36%，1.38%，符合精度要求.基准罐体的时间步长和受力进行修正后，与一般圆柱及椭圆形罐体受力的大小和规律基本一致;对于作横向运动的柱形罐体，受力大小与罐体长度成正比.通过修正基准罐体的时间步长和受力，对一般圆柱及椭圆形罐体的受力也可实现BP神经网络的预测，为罐车动力学分析快速有效地提供所需数据.

BP神经网络;液体晃动;罐体;受力

罐车在不平路面上颠簸行驶时，不可避免会出现摆动，特别是在紧急转弯、躲闪、移线等不稳定变速行驶过程中，由于罐车横向运动状态的改变，会引起液体发生横向大幅晃动，液体重心将严重偏移，极易发生翻车事故.因此研究罐车的横向稳定性问题，具有重要的实际意义.

研究罐车液体横向晃动问题的一些经典方法是结合势流理论和车辆动力学，建立罐车-液体耦合简化模型，用直接耦合方法研究液体晃动力及对罐车横向稳定性的影响［1－3］，这种方法由于基于势流理论只能处理理想流体的小幅晃动，处理不了粘性流体的大幅晃动现象;用VOF(Volume of Fluid)模型数值计算自由液面形态变化［4－5］，可以处理粘性流体的大幅晃动问题，但前提条件是已知罐车运动加速度的时间历程.由于液体、罐车之间存在着典型的刚-液耦合作用，一般情况下不可能预知罐车运动加速度的时间历程.又由于罐车系统的复杂性，解决液体、罐车之间耦合作用的一种可行方法是顺序耦合方法，即独立求解流体域和罐车的多刚体运动，以刚-液耦合界面之间传递变量的方式，在数值上多次迭代实现罐车充液系统的相互耦合.这种方法对液体和罐车运动情况都可以准确计算，但是需要随时数值模拟液体晃动及传递流体-罐车之间的数据，效率较低.

根据文献［4－5］，罐体受力决定于之前自由液面形态和即将经历的加速度，但是自由液面形态很难捕捉和描述.由于罐体受力和液体晃动形态存在一定的对应关系，并且晃动液体具有惯性，研究发现，通过前两时刻的罐体受力、加速度及将要经历的加速度可以较准确地预测下一时刻的罐体受力.本文利用这一关系，预测罐体受力，省略了流体计算，为罐车动力学分析快速有效地提供所需数据.

1 计算模型及计算方法

1.1 控制方程组

本文采用VOF模型处理罐内气液两相湍流流动现象，控制方程组包括连续方程和动量方程.

式中，u为速度;p为压强;a为加速度.由于采用了VOF模型，ρ和μ分别为容积分数的平均密度和动力粘性系数.

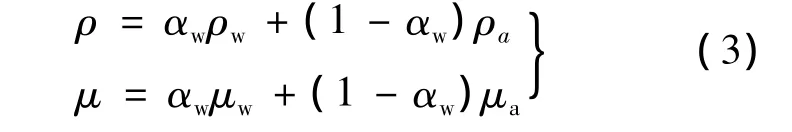
式中，αw为液体的容积分数;ρw和ρa分别为液体和气体密度;μw和μa分别为液体和气体动力粘性系数.

1.2 基准罐体模型及网格划分

本文以某型号液罐单室为研究对象，罐体截面为圆形，前后封头均为平封头，直径为2254mm，长2150mm，如图1所示，在本文中该形式单室定义为基准罐体.坐标原点位于左侧端面的圆心，x轴指向汽车前进方向且平行于地面，z轴垂直地面向上，y轴平行于地面向左.对此计算模型采用结构六面体网格，网格数在4万左右，如图2所示.

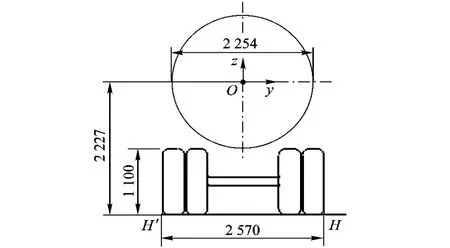
图1 罐车模型示意图

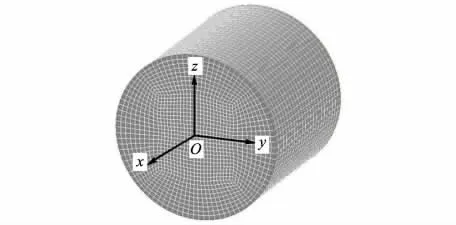
图2 单室模型及网格划分

1.3 边界条件及初始条件

罐体及防波板表面设置为无滑移壁面边界条件.初始时气液交界面平行于xy平面，液体和气体相对罐体速度为0，气体压强为1×105Pa.

1.4 求解方法及计算参数

速度和压强的耦合处理方法采用PISO方法，压力修正方程的离散格式采用Body Force Weighted格式，对流项离散格式采用一阶迎风格式.

罐体内材料为空气和油，空气视为不可压气体，密度为 1.205 kg/m3，动力粘性系数为 1.81 ×10－5kg/(m·s);油的密度为 830 kg/m3，动力粘性系数为3.32×10－3kg/(m·s).非定常计算中时间步长为0.0005 s.

2 数值计算方法验证

罐车做变加速行驶时，液体晃动现象复杂，不易进行试验验证，因此本文对做横向运动的罐车突然静止后，液体晃动频率的数值计算结果与试验结果［6］进行对比，以验证本文数值计算方法的可靠性.

文献［6］中的模型为圆柱容器，长为0.31m、半径为0.145m，容器内流体介质为空气和水.本文共计算了从0.2～0.8 7种不同充液比下的液体横向晃动频率，与实验值列于表1中，可见，计算值与实验值误差都在7.27%以内，因此认为本文所采用的数值计算方法基本准确.

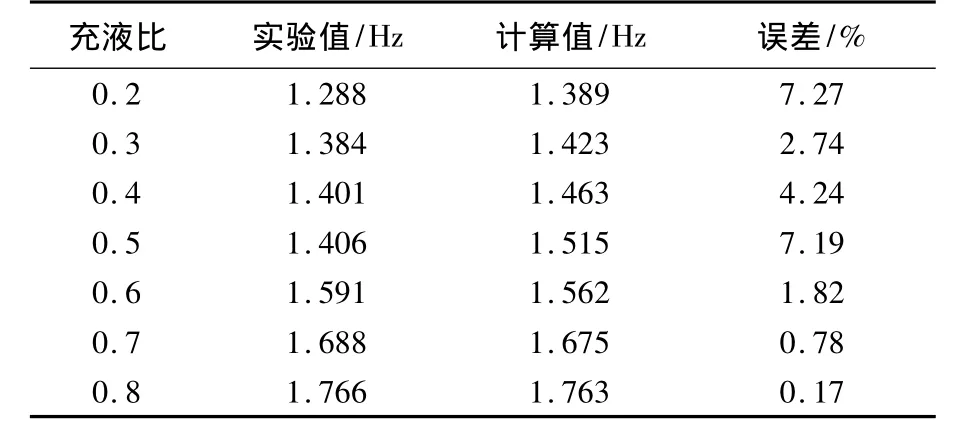
表1 各充液比下计算值与实验值的对比

3 基准罐体受力BP神经网络预测

3.1 力的影响因素

将充液比K、前两时刻(N－1和N)罐体受力Fy(N－1)，Fz(N－1)，MN－1，FyN，FzN，MN，加速度 aN－1，aN及将要经历的加速度aN+110个元素作为输入层节点，下一时刻(N+1)罐体受力 Fy(N+1)，Fz(N+1)，MN+13个元素作为输出层节点，对罐体受力进行预测.本文Fy为罐体横向受力，Fz为垂向力，M为过H点且平行于x轴的侧倾力矩(当Fy为负值时，M为过H'点且平行于x轴的侧倾力矩)，见图 1.

3.2 训练样本

本文使用一组实验测得的罐车横向变加速度数据作为加速度变化的依据，该数据在6.8 s时间内，罐车的横向加速度变化范围在－0.5～1.2m/s2，而且在 0.1 s内变化不超过 ±0.1m/s2.据此确定仿真计算横向加速度的变化范围和每0.1 s变化的范围.再对不同加速度变化过程进行仿真计算，让数据更加丰富，分布更加合理.在数值计算过程中，加速度每0.1 s改变一次，模拟罐车转弯、躲闪、移线等变速行驶状态.

利用计算得到的数据，尽量合理地选取共221个数据作为训练样本.以主要目标输出值横向受力Fy(N+1)为例，如表2所示，为各个受力范围内的训练样本个数.充液比较小时，罐内液体晃动造成罐体受力的变化范围也较小，使得某些范围的数据缺少.除此之外，训练样本基本包含了整个受力范围.

表2 不同受力范围内训练样本个数

所建立的BP神经网络模型为3层网格，隐含层的神经元数目为37个.

根据人工神经网络模型，构建罐车液体晃动受力预测模型.设定样本误差性能函数 SSE(Squared Sum Error)误差平方和的目标值为1×10－4.

3.3 模型预测及误差分析

在网络训练完成后，用158个数据作为检验样本，验证网络预测的可靠性.

由训练结果可知，对Fz(N+1)预测最为准确，最大误差为0.36%，平均误差为0.065%.原因是垂直方向主要受重力加速度作用，罐车横向加速度相对较小，液体晃动对垂向力的影响小，因此垂直力改变较小.

罐体侧倾力矩 MN+1的最大预测误差为1.38%，平均误差为0.26%，也比较小.由于影响MN+1的因素为 Fy(N+1)和 Fz(N+1)，以及力的作用点，Fy(N+1)远小于 Fz(N+1)，并且Fz(N+1)变化不大，同时液体晃动幅度不是很大，力的作用点偏移也不是很大，所以侧倾力矩变化也较小.

Fy(N+1)最大误差值为8.88%，平均误差为1.73%，误差较大.Fy(N+1)为罐体的横向受力，随着充液比、加速度和液体晃动状态的改变，变化较大，导致计算误差也较大.下面重点分析Fy(N+1)的预测结果.

表3给出不同充液比时Fy(N+1)预测值的统计情况，其中平均误差是各组误差绝对值的平均值.可知，训练样本较多的情况下，平均预测误差较小，且各误差大小比较接近;由于没有充液比为0.8，0.7 和0.55 3 种训练样本，这 3 个检验预测值平均误差较大，但是Fy(N+1)的预测值误差仍然符合精度要求，可见BP网络具有相当强的泛化能力和非线性函数逼近能力.对充液比0.33和0.9的情况预测误差较大，原因是这2个充液比可以参照的数据较少.

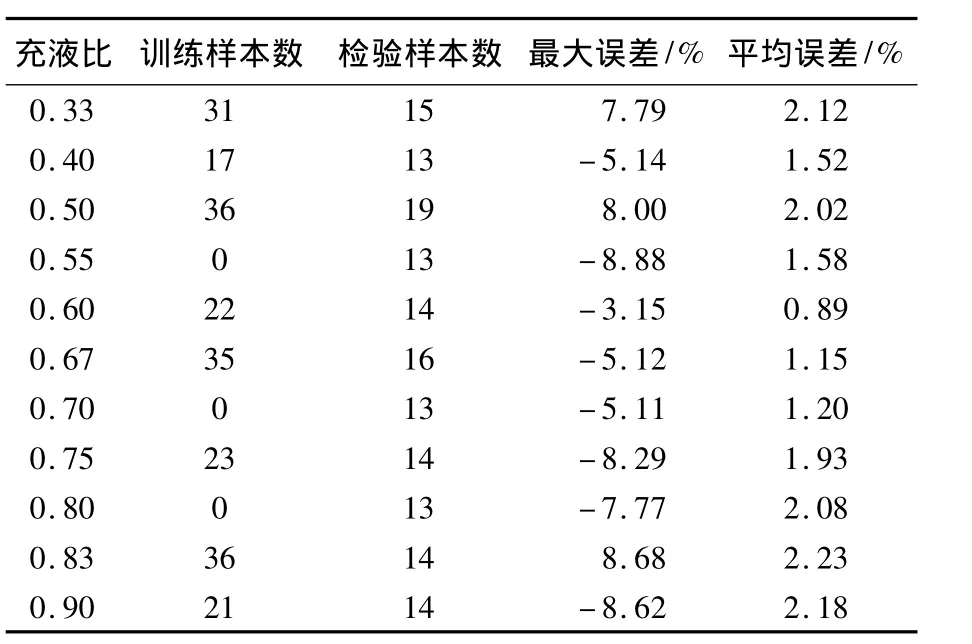
表3 不同充液比样本数和误差值

表4是对检验样本Fy(N+1)的预测值进行范围划分.由该表可知，选用的检验样本是比较全面的，基本反映了各种晃动情况.

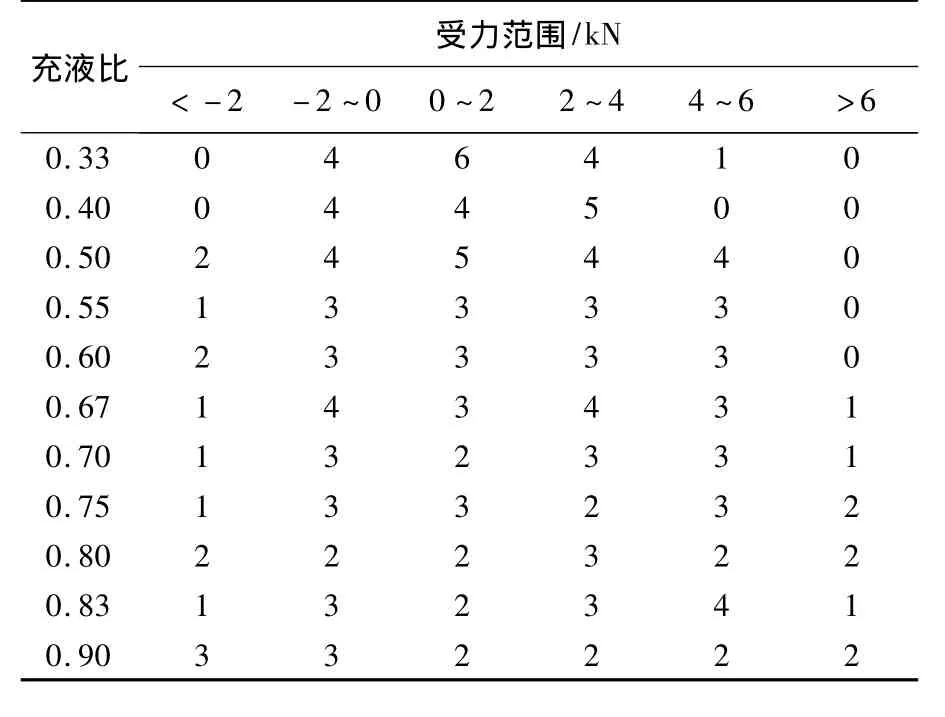
表4 不同受力范围内检验样本个数

通过分析，证明使用BP网络对罐车内液体晃动时的受力预测是可以实现的.进一步精选和扩充训练样本，可以使预测达到更高的精度.

4 不同尺寸及形状罐体受力的预测

4.1 不同直径圆柱罐体

本节预测不同直径圆柱罐体的受力，该圆柱罐体长度等于基准罐体长度.根据研究发现，对于圆柱罐体，罐体直径对液体晃动周期有较大影响，依据周期确定的时间步长对于准确预测罐体受力至关关键.因此，必须先计算不同直径圆柱罐体内液体自然晃动周期.表5所示充液比为0.4的结果，其中直径比值为该罐体直径与基准罐体直径的比值，周期系数为该罐体内液体横向晃动周期与基准罐体的比值.

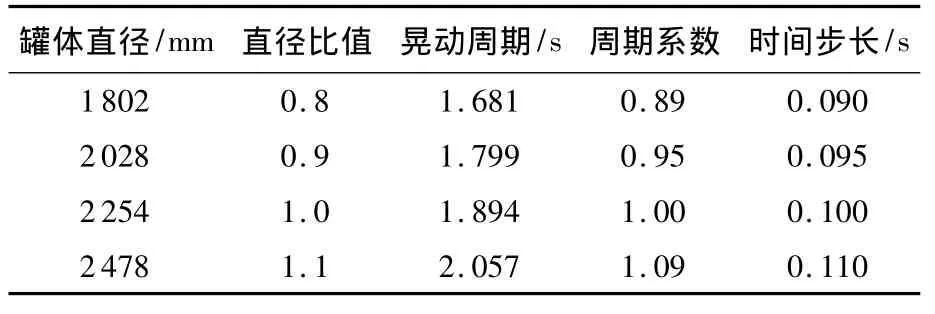
表5 充液比0.4时不同直径圆柱罐体的参数

由于基准罐体以0.1 s为时间步长，为其周期系数的1/10，则其他直径罐体的时间步长也为本身周期系数的十分之一.为处理方便，对计算出的时间步长取整，则得表5所示的结果.

图3给出直径比值为0.8时的数值计算值与修正值的对比情况，其中计算值为根据表5的时间步长进行数值计算时的结果，修正值为该罐体直径比值的平方与基准罐体横向受力的乘积，可知两者大小和变化规律符合较好.另2个直径比值0.9和1.1也有同样的结果.

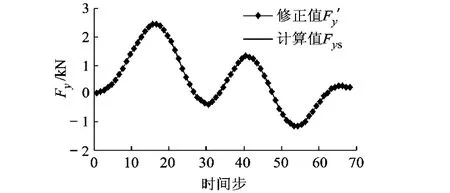
图3 直径比值为0.8时修正值与数值计算值的对比

还对充液比为0.8的情况进行了研究，结果显示也都遵循上面的规律.进一步的研究还发现，垂向力及侧倾力矩也都遵循上面的规律.

4.2 长轴为2254mm的椭圆形罐体

本节预测不同短轴椭圆形罐体的受力，该椭圆形罐体长度等于基准罐体长度，长轴等于基准罐体直径2254mm.根据研究还发现，对椭圆形罐体，短长轴比值(短轴与长轴的比值)对液体晃动周期有较大影响.表6所示充液比为0.5的结果，周期系数的定义及时间步长的算法同上.

表6 充液比0.5时不同短轴椭圆形罐体的参数

图4给出直径比值为0.6时数值计算值与修正值的对比情况，其中计算值为根据表6的时间步长进行数值计算的结果，修正值为该罐体短长轴比值与基准罐体横向受力的乘积，可知两者大小和变化规律符合较好.另2个短长轴比值0.67和0.7也有同样的结果.

充液比为0.75及垂向力、侧倾力矩的情况也都遵循上面的规律.

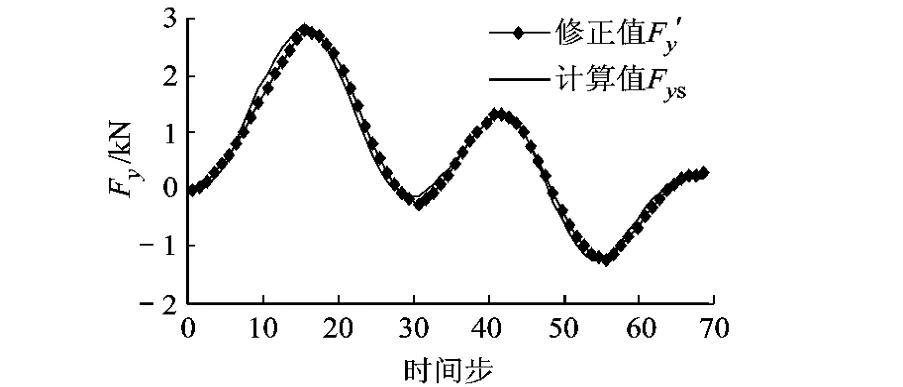
图4 短长轴比值为0.6的修正值与数值计算值的对比

4.3 一般椭圆形罐体

本节预测一般椭圆形罐体的受力.当一般椭圆形罐体长度与基准罐体不同时，通过研究发现，对于作横向运动的柱形罐体，受力大小与罐体长度成正比.因此结合上两节的研究结果，通过修正基准罐体的时间步长和受力，即可预测一般椭圆形罐体的受力.

主要通过如下几方面的修正:①针对直径等于椭圆长轴的圆柱罐体的时间步长及受力进行修正;②针对一般椭圆形罐体的短轴对时间步长及受力进行修正;③针对一般椭圆形罐体的长度对受力进行修正;④对给定充液比进行插值处理.

5 结论

对圆柱基准罐体进行了受力预测，横向力、垂向力和侧倾力矩最大预测误差分别为0.36%，8.88%，1.38%，符合精度要求.

基准罐体的时间步长和受力进行修正后，与一般圆柱及椭圆形罐体受力的大小和规律基本一致.对于作横向运动的柱形罐体，受力大小与罐体长度成正比.通过修正基准罐体的时间步长和受力，即可用BP神经网络预测一般圆柱及椭圆形罐体的受力.

References)

［1］李松.油罐车液体晃动动力特性研究［D］.四川:西南交通大学力学与工程学院，2006 Li Song.Study on dynamic characteristicsof liquid sloshing in an oil tank train［D］.Sichuan:School of Mechanics and Engineering，Southwest Jiaotong University，2006(in Chinese)

［2］卢军.任意充液比油罐车液体晃动及整车横向稳定性研究［D］.四川:西南交通大学力学与工程学院，2009 Lu Jun.Liquid sloshing and transverse stability analysis of tank truck［D］.Sichuan:School of Mechanics and Engineering，Southwest Jiao Tong University，2009(in Chinese)

［3］ Hasheminejad SM，Aghabeigi M.Liquid sloshing in half-full horizontal elliptical tanks［J］.Journal of Sound and Vibration，2009，324:332 －349

［4］陈志伟.移动式压力容器介质晃动数值模拟及防波装置研究［D］.浙江:浙江大学材料与化学工程学院，2006 Chen Zhiwei.Numerical simulation of liquid sloshing in transportable pressure vessel and research on the baffles［D］.Zhejiang:College of Chemical Engineering and Materials Science，Zhejiang University，2006(in Chinese)

［5］刘奎，康宁.罐车转向时液体晃动的仿真分析［J］.北京航空航天大学学报，2009，35(11):1403 －1407 Liu Kui，Kang Ning.Simulation of liquid slosh in turning process of tank truck［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(11):1403 －1407(in Chinese)

［6］李松，高芳清，杨翊仁，等.液体晃动有限元模态分析及试验研究［J］.核动力工程，2007，28(4):54－57 Li Song，Gao Fangqing，Yang Yiren，et al.Finite element modal analysis and dynamic experimental for liquid sloshing［J］.Nuclear Power Engineering，2007，28(4):54 －57(in Chinese)

(编 辑:张 嵘)

Prediction of lateral liquid sloshing force of tank based on neural networks

Kang Ning Jia Jia Liu Xiandong

(School of Transportation Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

Numerical simulation of liquid sloshing force under lateral acceleration of reference tank was conducted with volume of fluid(VOF)model of fluent software.Liquid filling ratio，forces，acceleration were set as inputs，while forces after a few seconds as targetoutputs.Reasonable distributed results were selected as training samples to establish prediction model of liquid sloshing forces acting on the reference tank.This trained BP neural networks were tested by 158 various samples.The maximum prediction errors of vertical force，lateral force and lateral moment were 8.88%，0.36%，and 1.38%.The magnitude and regulation of the modified time step and forces of reference tank are nearly the same as general cylindrical tanks;The magnitudes of forces are proportional to the length of cylindrical tank in lateral motion.Through revising the time step and forces of reference tank，the forces of general cylindrical tank can be predicted based on BP neural network.The study can provide the necessary data for the analysis of tank truck dynamics efficiently.

BP neural networks;liquid sloshing;tank;forces

U 469.6

A

1001-5965(2011)06-0649-05

2010-04-09

康 宁(1963－)，女，辽宁金州人，副教授，kangning@buaa.edu.cn.