基于自适应UKF的敏感器故障诊断算法
2011-03-15董云峰
胡 迪 董云峰
(北京航空航天大学 宇航学院,北京 100191)
基于自适应UKF的敏感器故障诊断算法
胡 迪 董云峰
(北京航空航天大学 宇航学院,北京 100191)
针对非线性系统中敏感器测量过程存在异常干扰和出现仪器故障问题,提出一种基于自适应UKF(Unscented Kalman Filtering)的鲁棒故障诊断算法.算法通过新息特性分析引入自适应矩阵对异常干扰和仪器故障建立系统级抑制和部件级诊断.系统级检测将UKF的新息特性通过自适应函数引入状态预测,修正异常值对状态预测值的影响,达到对异常干扰的鲁棒性.部件级检测将新息特性分解成各部件参数的新息特性,建立各自敏感器的自适应矩阵,通过对自适应矩阵的迹进行判断,检测是否发生故障并隔离故障.仿真结果表明,算法对异常值具有较强的鲁棒性,对测量仪器失效造成的故障能够准确地检测并给出故障大小.算法结构简单,计算量小,对工程应用具有较好的参考价值.
非线性系统;鲁棒性;敏感器故障诊断;故障检测;卡尔曼滤波;姿态控制
对于某些非线性系统来说,模型的建立并不能精确反映系统的特性,一些由外部干扰引起的模型的不确定性对系统有着非常重要的影响.这种不确定性反映在测量值有时候会出现异常,或者是野值,当异常或野值经过一段时间后消失,可认为其为一种可修复性故障,可以采用鲁棒滤波器对其抑制,避免其对系统造成重大影响.
故障诊断算法可以通过观测器方法[1]实现,也可采用基于滤波器的方法实现.卡尔曼滤波是采用最小协方差的形式达到对状态的最优估计,在故障诊断方面有着重要应用,如文献[2]采用一种自适应卡尔曼滤波应用于航天器姿态估计的故障诊断,文献[3]利用扩展卡尔曼滤波(EKF,Extend Kalman Filtering)能够对非线性系统进行状态估计的特点进行故障诊断,文献[4]将未知输入观测器方法引入EKF,提出UIEKF(Unknown Input EKF)方法.但是EKF需要计算系统的雅可比矩阵,对于大多数非线性系统来说计算量非常大.文献[5]提出了UKF(Unscented Kalman Filtering),采用Sigma点状态变量进行采集,不需要计算雅可比矩阵,并且对于系统的表现形式也没有更多的要求,因此UKF被应用到很多方面.在故障预测方面[6],文献[7]也提出采用自适应因子用于校正预测状态变量误差协方差,并将其应用于故障预测当中,但自适应因子不适合于多变量系统.文献[8]提出了一种修改滤波增益的方法,其提出的滤波增益矩阵,可适合多变量系统,对测量变量进行各自修正,从而达到滤波稳定的效果.
本文在文献[8]的基础上,提出在滤波新息特性的基础上,通过对自适应矩阵的迹的检测实现对系统测量异常值的判断,并引入自适应函数来修正对状态变量的预测,从而抑制异常值对系统的影响.通过自适应矩阵对干扰和故障建立两级检测即系统级检测和部件级检测,系统级检测只需对发生的异常进行判断是否为野值,如果是异常干扰将对异常干扰进行抑制否则进入部件级检测,部件级检测中每个敏感器均有自适应矩阵,对矩阵的迹进行检测来判断是否出现故障,对产生的残差评价即可知故障的大小及分布形式.文中针对卫星姿态确定系统敏感器测量存在干扰及故障问题,通过设置异常值和测量仪器故障分布函数,采用自适应UKF进行仿真.仿真结果表明,算法对出现的干扰有较强的鲁棒性,对出现的故障通过各敏感器自适应矩阵能较好地实现故障检测与隔离,通过残差的评价可以计算出故障的大小范围及分布情况.
1 问题描述
1.1 自适应UKF
考虑如下带有未知扰动的非线性系统:
式中,x∈Rn表示状态量;u∈Rp表示输入;d∈Rq表示未知扰动或野值、模型不确定性;y∈Rm表示测量输出;f表示非线性函数;C表示系数矩阵;
k(xk)表示未知干扰的分布函数.
标准的UKF在测量模型与仪器模型非常匹配时工作非常好,当测量出现非正常值或者当仪器测量过程受外界影响测量值发生飘移等时,标准的UKF没有将测量误差反映到滤波过程中,因此会对状态估计产生较大的偏差影响[4],而自适应算法可以在出现异常情况时将状态估计进行实时校正.
定义测量值与估计值的残差为

当测量仪器正常时,满足如下方程式[5]:

式中,μ为滚动窗口;Pyy为测量估计方差;R为测量噪声方差矩阵.
当出现测量野值时,方程式(3)左右两边将不再相等,因此可定义自适应矩阵满足S(k)下列式子:
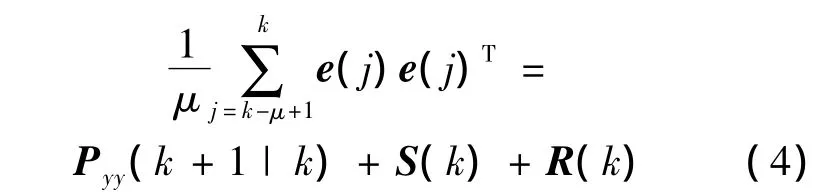
从而可得

式中,S(k)的统计特性服从χ2分布;通过检测S(k)的迹可知是否存在非正常值:

式中m为测量变量个数.
定义如下函数用于校正状态估计:

从而状态估计修正为

通过式(7)即可对敏感器测量过程中存在非正常数据进行校正,由于S(k)包含了新息特性,因此式(7)在状态预测之前就会自适应调整,配合标准UKF,即式(5)~式(8)组成自适应UKF.
1.2 故障诊断
自适应UKF可以对非正常数据进行校正,但对故障也存在一定的抑制性,对于如下含有干扰及敏感器故障的非线性系统:

式中F(x)为故障函数并定义当干扰d持续时间超过N时,可认定其为一种故障.
因此当系统式(9)经过自适应UKF后,系统可简化为

对于系统式(10),采用如图1所示的残差生成策略,通过自适应矩阵建立两级检测器.在系统级建立自适应矩阵用来抑制异常干扰对系统的影响,当故障产生时,系统级检测器向部件级检测器产生故障报警.部件级检测通过对UKF新息特性的分解,针对每一个敏感器均设计一个只与其敏感器参数相关的自适应矩阵,自适应矩阵仍可以采用式(5)产生,只需将协方差矩阵和噪声方差矩阵更换成这个敏感器测量参数的协方差矩阵以及噪声协方差矩阵即可,采用式(6)即判断此敏感器是否发生故障.
故障的大小可采用式(11)进行计算.


图1 残差评价策略
通过上述残差生成及评价方法即可判断是什么敏感器发生了故障,并可求出故障大小.
由于产生的残差是采用UKF的新息特性,每一个变量均可反映出其对应敏感器的故障状态.
2 仿真研究
2.1 系统模型及参数设置
本文在文献[9]的基础上采用星敏感器和陀螺作为测量设备,星体运动学方程和动力学方程[10]为

陀螺测量模型为

具体定义参考文献[9].
矢量测量模型:

具体定义参考文献[9].
则可定义如下系统,取x=[q ω]T:

设定外部干扰力矩和输入控制力矩均为量级为10-4的高斯白噪声.星体惯量设为

初始星体四元数为 q=[0.5,0.5,0.5,0.5],(°),初始星体估计四元数为(°),初始星体角速度 ω =[0.1,0.1,0.1],(°)/s,初始星体估计角速度为采样时间间隔1 s.
2.2 自适应函数对干扰的抑制
设定星敏感器在第40 s~第50 s发生异常值,异常分布函数设定如下:

由式(5)得出系统自适应矩阵的迹的对比图如图2所示.
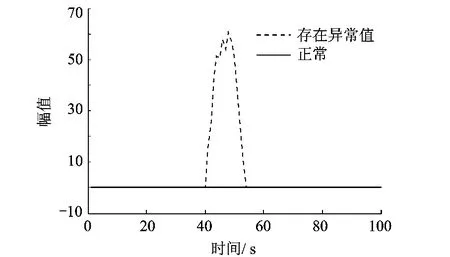
图2 系统自适应矩阵的迹
从图2所示可以清楚地看出,当出现异常值时,自适应矩阵的迹会发生很明显的偏差,而在正常状态下其迹是约等于0,当异常结束时,自适应矩阵的迹约又会回归至0,因此可通过迹的判断来断定是否存在异常值.
图3表明了当系统采用UKF和自适应UKF对异常处理的情况,图中表明在没有异常值时,UKF能最优估计出状态变量,因此姿态角误差为0.当出现异常值,而没有相应的自适应函数时,姿态出现偏差,而对卫星姿态系统来说是不允许出现这么大异常偏差的;当采用自适应UKF,存在自适应函数式(6)时,可通过自适应函数修正预测状态变量,姿态角误差接近于0,表明自适应函数对异常值具有较强的鲁棒性.

图3 姿态角误差和姿态角速度误差
2.3 故障诊断
系统采用星敏感器和陀螺敏感器进行姿态测量,其中星敏感器用于测量姿态角,陀螺分为x,y和z轴陀螺沿星体主轴分布,用于测量x,y和z轴的姿态角速度.
设定星敏感器在第60 s时发生故障,故障函数如式(17)所示.

设定x轴陀螺在100 s时发生故障,故障函数如式(18)所示.
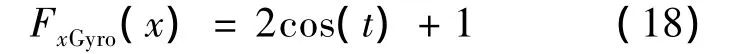
图4是系统级自适应矩阵的迹图,从图中可以看出,系统在40 s~50 s之间发生了干扰,也就是上一节所述的对干扰的抑制,从60 s开始发生了一个故障,而从100 s后又发生了一个故障,从故障持续的时间来看,超过了设定值20 s,产生故障报警.
图5是各敏感器的自适应矩阵迹图.

图4 系统自适应矩阵迹

图5 各敏感器自适应矩阵迹图
从图5中可以看出,系统对于20 s以内的干扰可以有效地抑制没有传入敏感器的自适应矩阵当中.从矩阵迹图可以看出,星敏感器和x轴陀螺均发生了故障,而y和z轴陀螺没有发生故障,并且可以看出星敏感器先于x轴陀螺发生故障,由于已经持续了20 s时间,因此系统矩阵产生了故障报警,所以x陀螺在100 s处发生故障后,其信息直接传入了陀螺的自适应矩阵中,由此可见,自适应矩阵能准确地检测出敏感器是否发生故障及故障发生的时间.
图6是产生的新息特性,由图中可以知道目前星敏感器及x轴陀螺敏感器发生的故障大小及特性.

图6 各敏感器产生的新息特性图
3 结论
本文提出一种自适应UKF算法,用于敏感器的故障检测与隔离.通过对测量新息特性分析引入自适应矩阵,分别针对异常干扰和仪器故障建立系统级和部件级检测器,根据不同级别检测器中的自适应矩阵迹的判断可得出敏感器测量值是否出现异常值或是故障,然后通过自适应函数和残差生成策略抑制异常干扰和诊断故障.仿真结果表明,算法对异常值具有鲁棒性,通过自适应矩阵迹可对各敏感器产生的故障准确地诊断.算法通过修正UKF的新息特性实现,计算简单,对工程应用具有参考价值.
References)
[1]金磊,徐世杰.基于扩张状态观测器的飞轮故障检测与恢复[J].北京航空航天大学学报,2008,34(11):1272 -1275 Jin Lei,Xu Shijie.Extended sate observer-based fault detection and recovery for flywheels[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(11):1272 - 1275(in Chinese)
[2] Mehra R,Seereeram S,Bayard D,et al.Adaptive Kalman filtering failure detection and identification for spacecraft attitude estimation[C]//Proceedings of the 4th IEEE Conference on Control Applications.Albany:IEEE,1995:176 -181
[3] Wang Xudong,Syrmos V L,Fault detection,identification and estimation in the electro-hydraulic actuator system using EKF-based multiple-model estimation[C]//16th Mediterranean Conference on Control and Automation.Ajaccio:IEEE,2008:1693 -1698
[4] Li Linglai,Zhou Donghua,Wang Youaing,et al.Unknown input extended Kalman filter and applications in nonlinear fault diagnosis[J].Chinese Journal of Chemical Engineering,2005,13(6):783-790
[5] Julier S J,Uhlmann JK,Durrant-Whyten H F.A new approach for filtering nonlinear system[C]//Pro of the American Control Conference.Seattle:IEEE,1995:1628 -1632
[6]张磊,李行善,于劲松,等.一种基于二元估计与粒子滤波的故障预测算法[J].北京航空航天大学学报,2008,34(7):798-802 Zhang Lei,Li Xingshan,Yu Jinsong,et al.Fault prognostic algorithm based on dual estimation and particle filter[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(7):798-802(in Chinese)
[7] Cao Yuping,Tian Xuemin.An adaptive UKF algorithm for process fault prognostics[C]//2009 Second International Conference on Intelligent Computation Technology and Automation.Changsha:IEEE,2009:487 -490
[8] Soken H E,Hajiye C.Adaptive unscented kalman filter with multiple fading factors for pico satellite attitude estimation[C]//RAST'09.4th International Conference on Recent Advances In Space Technologies.Istanbul:IEEE,2009:541 -546
[9] Crassidis JL,Markley F L.Unscented filtering for spacecraftattitude Estimation[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Texas:AIAA,2003:11 -14
[10]章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998:148,172 Zhang Renwei.Satellite orbit & attitude dynamics and control[M].Beijing:Beihang University Press,1998:148,172(in Chinese)
(编 辑:张 嵘)
Sensor fault diagnosis algorithm based on adaptive UKF
Hu Di Dong Yunfeng
(School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
To the questions of the abnormal values and the instruments failures for the nonlinear sensor measurement systems,a robust fault diagnosis algorithm based on adaptive unscented Kalman filtering(UKF)was proposed.An adaptive matrix was produced according to the innovation of UKF,then a systems'detector and a parts'detector were built which were made use of restraining the abnormal values and diagnosing the instruments'faults respectively.The innovation of UKF was introduced to status prediction by the adaptive function for modifying the error efforts between the abnormal values and status predictive values and achieving the systems'robust,which was called systems'detector.The innovation was separated into the different sensors'parameters to produce adaptive matrix,which was formed the parts'detector.The trace of adaptive matrix wasmade use of detecting whether a fault or not and isolating the faults.The simulation results show that the algorithm is robust to the abnormal values,and is accurate to detect the faults from the sensor instruments and compute the range of faults at the same time.The structure of the algorithm is simple and less computational load,and is a good reference for engineering application.
nonlinear system;robustness;sensor fault diagnosis;fault detection;Kalman filtering;attitude control
V 448.21
A
1001-5965(2011)06-0639-05
2010-03-12
胡 迪(1984-),男,广西桂林人,博士生,hudibuaa@yahoo.cn.
