基于半光程差的天线反射面型面精度检测

周国锋 李晓星

(北京航空航天大学 机械工程及自动化学院，北京 100191)

基于半光程差的天线反射面型面精度检测

周国锋 李晓星

(北京航空航天大学 机械工程及自动化学院，北京 100191)

型面拟合最小量的选取是天线面板型面检测中的关键技术之一.天线表面各点半光程差的均方根是衡量天线型面精度的指标.根据圆锥曲面的几何定义及其光学性质，提出了圆锥曲面天线面板半光程差的直接计算方法，给出了基于半光程差的非线性最小二乘曲面拟合算法.以旋转抛物面天线面板为例，通过模拟和实际测量，对比分析了分别选取轴向误差和半光程差作为最小量拟合计算结果.试验验证了选取半光程差作为最小量拟合的算法具有更高的数值计算精度及稳定性.

半光程差;圆锥曲面拟合;非线性最小二乘;反射面型面检测

反射面天线的面型多采用旋转抛物面等具有良好光学性质的圆锥曲面.而天线面板的型面精度直接影响天线的工作性能［1］.根据文献［2］可知天线表面点的半光程差的均方根是衡量反射面天线精度的最佳指标.在实际应用中，通常通过测量天线面板上离散点三维坐标进行圆锥曲面拟合以获取被检测天线的型面精度情况.天线反射面的型面精度检测可以归结为求取型面参数及变换参数的非线性最小二乘问题，其中关键问题是采用何种最小量作为曲面拟合精度评价准则，文献［3］提出了一种改进的抛物面天线变形误差算法与评级方法，但该文章假设节点变形后的位置对拟合抛物面的法线和径向方向余弦近似等于原设计抛物面上相应位置的法线和径向方向余弦.文献［4］提出分块划分变形反射面，并采用Coons曲面拟合每个子域，利用周向三角拟合曲线与径向多项式拟合曲线来确定曲面片边界条件，再利用拟合曲面的法向误差评判该天线面板精度，该方法能反映反射面局部大变形，但文章利用拟合的Coons曲面的法向来代替口径面相位差.文献［5］对比分析了分别选取轴向、径向、法向、焦距等4种不同的最小量进行曲面拟合的计算结果.以上文献提出的方法和思路都能较好地评价型面的轮廓度，但都是利用其他量近似代替半光程差来衡量天线反射面精度.本文根据圆锥曲面的几何定义及光学性质，推导了圆锥曲面天线面板半光程差的直接计算方法，提出了基于半光程差的曲面拟合的非线性最小二乘拟合算法.最后以旋转抛物天线面板为例，通过模拟和实际测量，对比分析了采用轴向误差和半光程差作为最小量拟合的数值计算精度及稳定性.

1 半光程差的直接计算方法

1.1 半光程差定义

20世纪70年代，Ruse等就提出反射面表面半光程差的均方根是衡量反射面精度的指标，并在文献［2］中给出了计算半光程差的公式:

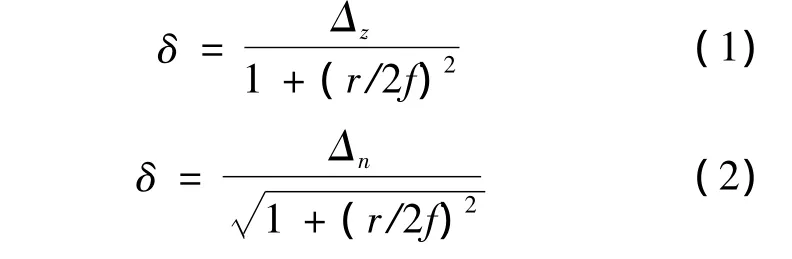
其中，Δz为轴向偏差;Δn为法向偏差;r为口径面半径;f为焦距.后来国内外的很多文献也推导出半光程差的计算公式，这些计算方法大多是推导了半光程差与其他偏差量(如轴向偏差或法向误差等)之间的计算关系.

图1为以抛物面天线为例，从焦点F发出的波，经过反射在前方形成一个等相位面，即对理论面上任意点A和P1有:

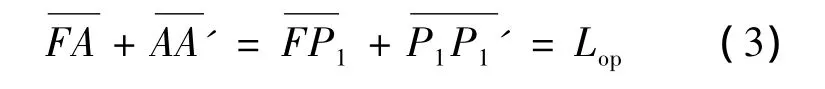
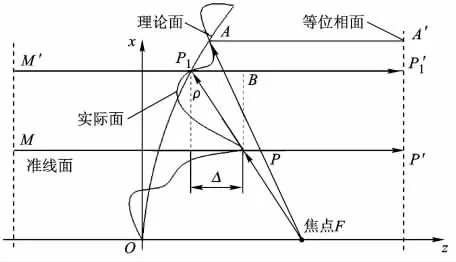
图1 抛物面半光程差

其中，Lop为从焦点到该等相位面的光程.对实际反射面而言，由于表面存在误差会引起天线口径面上各点电磁场产生相位差，使天线的旁瓣电平增高，增益降低.如在图1中，假设反射面在P点处凸出(凹的情况类似)，则从焦点F点射向P点到达等相位面上的电磁波所经过的光程与Lop之间的差值就是所谓的光程差，记作2δ.半光程差δ就是光程差的一半，对抛物面而言，从图1可得

1.2 圆锥曲面的半光程差

由于圆锥曲面良好的光学性能，在天线设计中经常采用抛物面作为主面，采用椭球面和双曲面作副面.根据圆锥曲线的轨迹定义:到定点的距离与到定直线的距离之比为常数e的点的轨迹，可知，当e=1时为抛物线有(图1):

又根据抛物线的光学性质:从抛物线的焦点发出的波，经过抛物线反射后，反射波都平行于抛物线的轴射出，可得到在凸出点P处有，代入式(4)和式(5)即可得到抛物面半光程差直接计算公式:

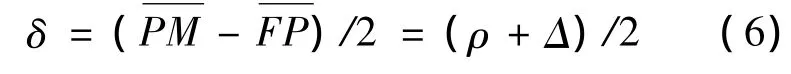
当e＜1时轨迹是椭圆(图2)，其光学性质为焦点发出的光，经过椭圆反射后，反射光线都汇聚到椭圆的另一个焦点上，即有，其中2a为椭圆的长轴，容易得

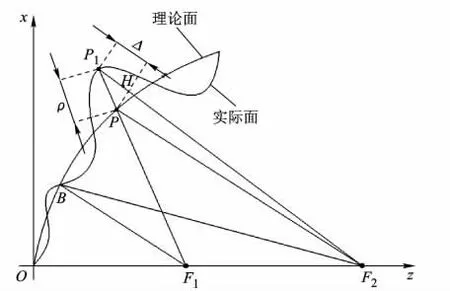
图2 椭球面半光程差

而当e＞1时为双曲线(图3)，从双曲线焦点发出的波，经过双曲线反射后，反射光线的反向延长线都汇聚到该双曲线的另一个焦点上，且有:

图3 双曲面半光程差

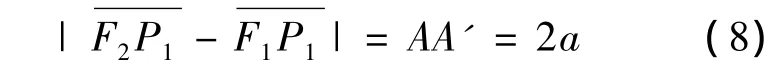
可以得到双曲面的半光程差计算公式为

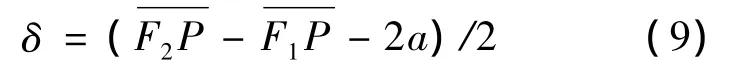
其中，2a为双曲线实轴长.

以上分析结合圆锥曲面的轨迹定义及光学特性，推导了抛物面等3种圆锥曲面的光程差的直接计算方法.

2 基于半光程差的拟合算法

2.1 坐标转换

在反射面精度检测过程中，型面测量点的三维坐标在测量坐标系下，因此进行曲面拟合时必须进行坐标转换.现假设m个测量点在测量坐标系下的测量坐标为(Xp，Yp，Zp)，在对应的设计坐标系下的理论坐标为(xp，yp，zp)，则根据文献［6］从测量点到理论点之间的转换关系为

其中，x0，y0，z0为沿测量坐标系的 x，y，z三轴的平移量，和绕测量坐标系的x，y，z三轴的旋转角α，β，γ并称为坐标变换六参数且有:

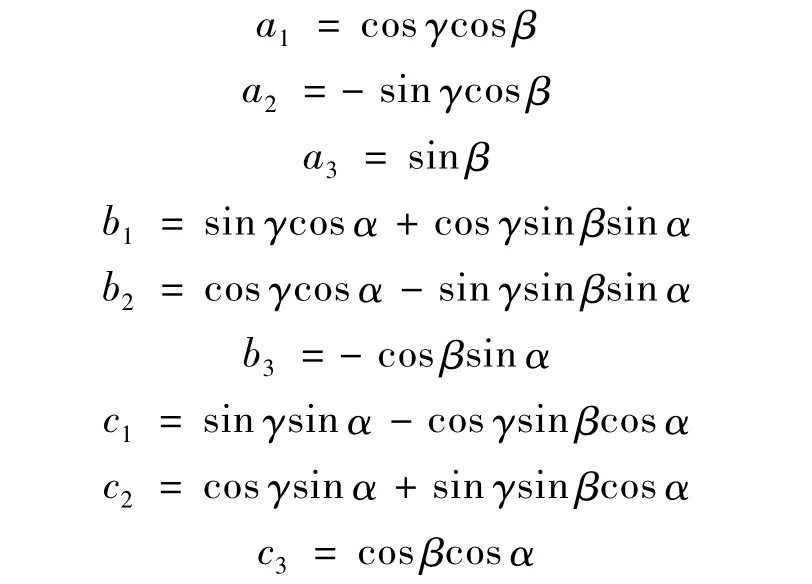
2.2 误差方程

如图2所示，设抛物线轴向为z轴，绕其旋转且焦距为f的二次抛物面理论方程为

其焦点理论坐标为(0，0，f)，其准线绕z轴旋转成的平面为z=－f，按照半光程差平方和最小原则拟合抛物面，根据式(6)直接列出基于半光程差误差方程为

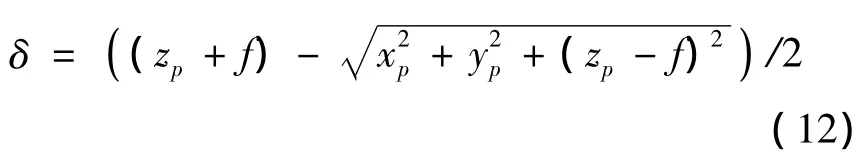
同理根据式(7)可以得到绕z轴旋转的椭球面光程差方程为

其中，2a为椭球长轴长.

根据式(9)可得绕z轴旋转的双曲面半光程差方程为

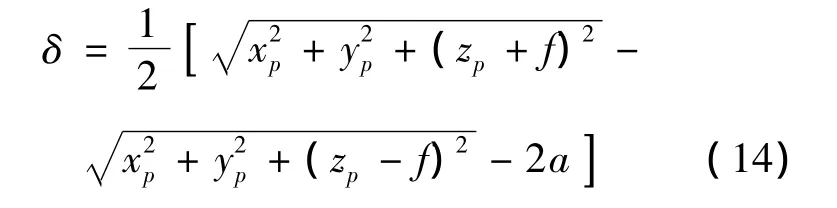
2.3 曲面拟合

其中，2a为双曲线实轴长.

如是曲面拟合问题转化为非线性最小二乘问题:

其中 x=(α，β，γ，x0，y0，z0，f)，f为焦距.采用Gauss-Newton法解决该非线性问题，主要迭代过程如下:

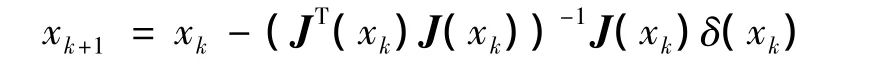
其中

得到解x*后，代入误差方程即可计算所有测量点基于半光程差的面板型面精度:

文献［5］分别以轴向偏差、径向偏差、法向偏差、焦距等4种不同的最小量，对抛物面天线测量数据进行了拟合，其中以轴向偏差平方和最小的原则拟合抛物面误差方程如下:

从计算结果可见采用4种不同最小量的拟合型面精度及转换参数有一定的差别，同时文献［7］研究结果表明以轴向偏差作为最小量的拟合算法对参数初值要求不严格，且计算速度快.故本文第3节将对比分析采用半光程差和轴向偏差作为最小量对某抛物面天线反射面进行试验验证.

3 试验验证

3.1 模拟试验

设有绕z轴旋转抛物面方程为式(11)，设其焦距f=4800mm，在其型面上按90m间距均匀取m=441 个采样点记为(xp，yp，zp)T，其中:

将(xp，yp，zp)T按给定参数变换后对上述的每个采样点增加服从三维正态分布的扰动σ=0.005mm，得到51组存在随机误差的旋转抛物面的模拟采样数据(Xp，Yp，Zp)T，p=1，2，…，51.按照第2节中介绍的方法计算型面精度，并将其中一组的计算结果列入表1，可以看出在扰动为σ=0.005mm的情况下，采用两种不同最小量的拟合旋转参数的相对误差在0.000 5°量级，平移参数的相互偏差在0.1μm量级，且有最终采用轴向误差计算的均方差为5.4μm，而采用半光程差计算的均方差为5.2μm.即在σ=0.005mm误差扰动下，两者计算精度差别很小.

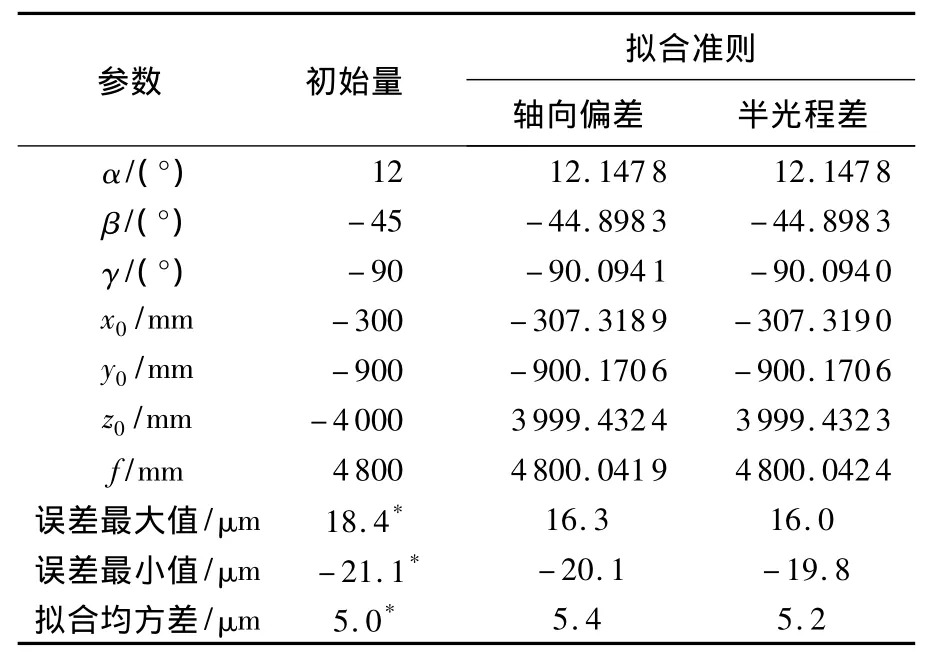
表1 模拟计算结果对比

3.2 误差分析

在反射面的实际检测中，影响反射面精度的因素主要包括测量误差和制造误差［8］，两种误差最终都耦合到测量点的坐标值上，假设单点坐标的最终耦合误差分别为Δx，Δy，Δz，根据多元误差传播计算公式，可以计算式(12)基于半光程差的单点处数值计算误差为

同理可计算式(16)基于轴向偏差的单点计算误差为

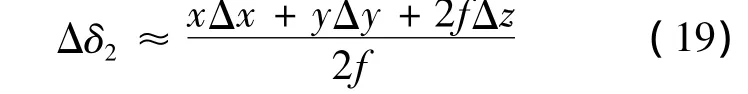
假设在Δx=Δy=Δz=σ的等精度条件下测量，其中σ为测量耦合误差，如代入限制条件式(17)得且一般有 z≪f，容易得到 Δδ1＜ σ ＜ Δδ2.故基于半光程差的算法有更好的数值稳定性.

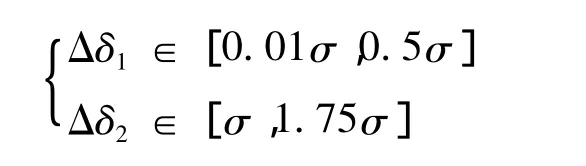
根据误差方程式(12)和式(16)，采用2.3节介绍方法拟合上述51组模拟采样点，计算结果如图4所示，可见在σ=0.005mm的等精度测量模型下，采用半光程差计算的最终均方差值比采用轴向误差的计算结果小0.2μm左右.图5表示扰动σ从0.005mm递增到0.255mm下的采用两种不同最小量的计算结果曲线，可见采用半光程差计算结果更接近随机扰动误差.同时发现当取σ=0.005mm时两者拟合均方差相差0.19μm，当σ取0.255 mm时两者拟合均方差相差11.7μm.

模拟试验表明:采用半光程差作为最小量的拟合准则具有更高的数值计算精度，在 σ=0.255mm误差扰动下，基于半光程差的算法具有更高的数值计算稳定性.

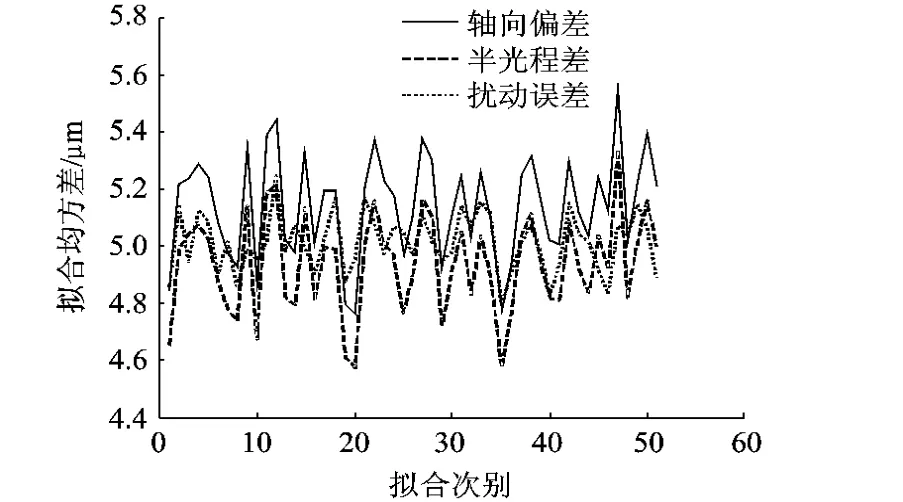
图4 σ=0.005mm等精度模拟测量结果

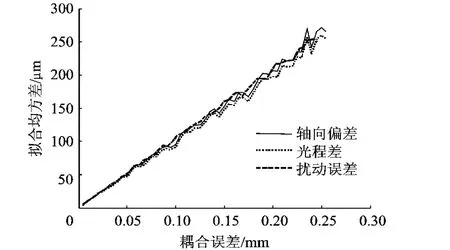
图5 变σ等精度模拟测量结果

3.3 反射面测量

北京航空航天大学研制的某型号高精度紧缩场，静区直径为2.5m，最高工作频率为40GHz.反射面为旋转抛物面，采用蜂窝夹层结构由多点柔性模加工而成［8］，反射面理论方程如式(11)，设计焦距 f=4 800 mm，单块面板尺寸为2112mm×2048mm.采用Leica AT901-B激光跟踪仪在反射面表面按90mm×90mm间距均匀采集n=5组测量点.

对测量数据分别选取轴向偏差和半光程差按照2.3节所述方法进行拟合处理，鉴于篇幅将其中3组数据的处理结果列于表2和表3.可以看出在实际的反射面精度检测中，采用轴向偏差及半光程差两者的拟合结果有一定差别，其中采用半光程差作为最小量拟合的型面拟合均方差值比前者小2μm，实际测量结果符合3.2节误差分析的结论.

表2 基于轴向偏差反射面测量结果

表3 基于半光程差反射面测量结果

4 结论

本文根据圆锥曲面的轨迹定义及几何光学特性，研究了基于半光程差的直接计算方法的反射面型面精度检测方法，以旋转抛物天线面板为例，通过数值模拟和实际测量，对比分析了采用半光程差作为最小量拟合的数值计算精度及稳定性，得到如下结论:

1)根据圆锥曲面的几何特征及光学特性，可以得到圆锥反射面的半光程差直接计算方法;

2)误差分析及模拟试验表明，采用基于半光程差作为最小量进行曲面拟合，在误差较大的情况下具有更好的数值计算精度;

3)实际测量表明，基于半光程差的检测方法能更真实地反映面板的实际精度，在高精度面板的实际生产检测及整体拼装调整量计算及精度预估中有实际应用价值.

致 谢 感谢课题组何国瑜教授在论文撰写过程中给予作者的大力支持.

References)

［1］ Anderson L J，Groth L H.Reflector surface deviations in large parabolic antennas［J］.IEEE Transactions on Antennas and Propagation，1963，11(2):148 －152

［2］ Ruze J.Antenna tolerance theory:a review ［J］.Proceeings of the IEEE，1966，54(4):633 －642

［3］王从思，段宝岩，仇原鹰，等.一种抛物面天线形状误差的合理评价方法［J］.上海理工大学学报，2006，28(1):14 －18 Wang Congsi，Duan Baoyan，Qiu Yuanying，et al.Improved evaluation for calculating shape errors of parabolic antennas ［J］.Journal of University of Shanghai for Science and Technology，2006，28(1):14 －18(in Chinese)

［4］王从思，段宝岩，仇原鹰.大型天线变形反射面的新拟合方法［J］.西安电子科技大学学报，2006，32(6):839 －843 Wang Congsi，Duan Baoyan，Qiu Yuanying.A novel method for fitting the distorted reflector of a large antenna ［J］.Journal of Xidian University，2006，32(6):839 －843(in Chinese)

［5］陈继华，李广云.离散点抛物面拟合的算法研究［J］.天线技术，2005，35(4):39 －43 Chen Jihua，Li Guangyun.Research on discrete points parabolic fitting algorithm［J］.Radio Engineering of China，2005，35(4):39－43(in Chinese)

［6］ Butler B P，Forbes A B，Harris PM.Algorithms for geometric tolerance assessment［R］.Technical Report DITC 228/94，1994

［7］张曦，胡春华，陈五一.二次曲面拟合与拟合参数不确定度分析［J］.北京航空航天大学学报，2006，32(9):1091 －1095 Zhang Xi，Hu Chunhua，Chen Wuyi.Quadratic surface fitting and uncertainty analysis of fitting parameters［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32(9):1091－1095(in Chinese)

［8］周贤宾，陈连峰，李东升.反射器夹层面板精密成形原理［J］.北京航空航天大学学报，2004，30(4):296 －300 Zhou Xianbin，Chen Lianfeng，Li Dongsheng.Principle of precision forming for sandwich panel of Large antenna reflector［J］.Journal of Beijing University of Aeronautics and Astronautics，2004，30(4):296 －300(in Chinese)

(编 辑:李 晶)

Base on semi-optical path difference of antenna reflector surface accuracy detection

Zhou Guofeng Li Xiaoxing

(School of Mechanical Engineering and Automation，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

The selection of minimum value of surface fitting is one of the key technologies refer to the antenna panel surface detection.The antenna surface root-mean-square of semi-optical path difference is an index of antenna surface accuracy.A direct calculation method of semi-optical path difference(OPD)was presented according to the geometric definition of conic surface and its optical properties.The nonlinear least squares curve fitting algorithm based on the semi-optical path difference was described.Employing a parabolic reflector panel as the sample，through simulation and actual measurements，the fitting results were contrastively analyzed while selected axial deviation and semi-optical path difference as minimum value respectively.The experiments verifying the fitting method based on semi-optical path difference is more precision and stability.

semi-optical path difference;conic surface fitting;nonlinear least squares;antenna surface detection

TN 820;TB 921

A

1001-5965(2011)06-0723-05

2010-07-08

北航D2025紧缩场研制项目

周国锋(1982 －)，男，湖南浏阳人，博士生，adian@me.buaa.edu.cn.