一种改进的局部多边形填充方法
2011-03-14许少华
许少华, 李 伟
(东北石油大学计算机与信息技术学院黑龙江大庆163318)
等值线图是一种离散数据的图形表示方法,在水利、土木、地质、石油勘探等工程和技术领域内广泛应用,已成为各研究领域的研究人员进行分析研究不可缺少的图件之一。等值带的填充就是用不同的颜色填充不同等值线围成的区域,使等值线图更直观反映二维数据特征,且美观清晰。在油田勘探开发和生产过程中,等值线图可以用来推断地质构造和地质分布参数,从而认识油气富集特征;也可直观的显示产油、含水等生产指标的分布情况,为油田生产方案调整提供依据。在传统的开发过程中,石油工程师一般根据现场测量数据进行手工绘制,不仅费时费力而且误差较大。随着计算机软硬件的发展,用于显示和绘制等值线图等其他地质图件的软件已被广泛用于石油勘探开发,为等值线绘制提供了很大的便利。但从模型和算法上改进相应的软件系统,提高绘图质量,还是十分必要的。
国内外对等值线的绘制已经有很多成熟的算法和软件,而对等值带填充的研究则相对较少。目前填充算法主要有:种子法、栅格法、拓扑填充、边界扫描等[1-4]。归纳起来可以分为两类:一类是先利用网格数据追踪等值线(等值带的边界),然后搜索连通区域进行填充;一类是根据网格化以后的数据,进行平面插值,使得绘图区域中当前设备分辨率下的每一个绘图像素点都有一个数据值,然后根据这个值给其所在的像素填上相应的颜色。第一类方法需要经过追踪和搜索两个步骤,算法复杂,实现困难;第二类方法实现简单但计算量跟绘图区域大小成正比。
庞世明等人提出一种局部多边形填充算法[5],其基本思想:是在每一个小矩形中按照填充颜色的级别将网格矩形分割为多个多边形,然后用相应的颜色进行填充,再进行网格范围的循环完成整个区域的填充。该算法的优点是不需要进行等值线的追踪,编程容易实现,计算量也较小。但是算法在搜索多边形时有以下不足:根据网格矩形各边等值点个数需要讨论多达12种情况,太过繁琐。
针对上述问题,本文提出一种改进的局部多边形填充方法。算法和庞世明等人提出的局部多边形填充算法类似,不需要进行等值线的追踪,将讨论情况精简为两种;且在多边形填充中时使用了凸包算法确定顶点的顺序,所以在搜索多边形时不用考虑点的空间位置,只需考虑各点对应的高程值。
1 算法实现
1.1 算法原理
首先通过插值算法,将离散数据网格化,得到网格各顶点处的坐标和高程值信息,然后逐一遍历每一个小矩形,在这些小矩形中按照填充颜色的级别计算等值点,找出其包含的多边形,最后用相应的颜色进行填充。
在搜索多边形时,首先计算出网格各边的等值点。因为不同高程值的等值线必不相交[6],并且一条等值线与矩形边的交点个数只有0、2、4三种情况,所以算法根据矩形网格中是否有一组或多组等值点的个数为4,分为两种情况讨论。如图1共有两组等值点,分别为EH和FG。图2也有两组等值点,EJ和FGHI,其中有第二组等值点个数为4,这种情况需特殊处理。由于插值算法,则等值点的权重同时也蕴含着与顶点间的距离,所以接着讲顶点和等值点按权重排序,然后按照一定规律即可将网格分割成多个多边形。
填充时,填充函数接收到的数组顶点是按照权重值排序的而不是二维平面内的坐标关系,因此若要填充多边形,还需要将这些顶点按照坐标关系按顺时针或者逆时针排序。这里应用二维凸包Graham算法来解决。Graham算法的描述:如果S为平面内的点的集合,Graham扫描算法从S中找出有最小的y坐标的点p(通过选出最左边的点打破平局)。然后根据点和p连线和正X轴所成的角度将S中的点排序[7]。详细实现过程这里不再赘述。填充颜色由多边形各个顶点高程值的平均在所在的颜色确定。
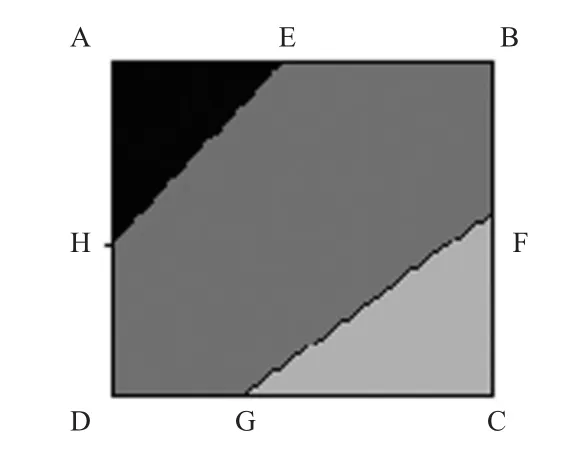
图-1等值点情况1Fig.1 Situation 1 of equivalent point
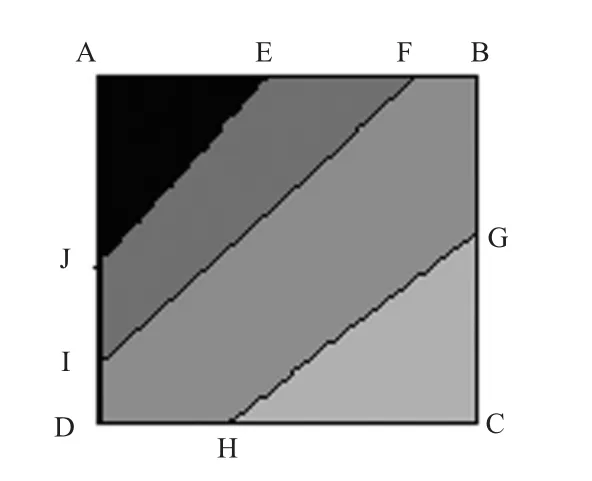
图-2等值线情况2Fig.2 Situation 2 of equivalent point
1.2 算法步骤
为实现算法,首先定义三个数组:AllFaces记录所有的网格矩形;AllPoints记录所有网格顶点;Found-Points记录每个网格中参与搜索多边形的点。两个类:ContourPoint类有3个属性,记录X,Y坐标和W(高程值)用于描述各矩形顶点和等值点;CountFace类有四个属性,记录一个矩形的四个顶点在AllPoints中的序号。
算法步骤如下:
Step 1:从AllFaces数组中取出一个元素。GOTO Step2。
Step 2:IF遍历结束
THEN退出程序;ELSE GOTOStep 3;
Step 3:清空FoundPoints数组。取出网格矩形四个顶点,根据级别定义,按顺时针从AB到DA(如图1)的顺序搜索各边上的等值点,并将顶点和等值点依次放入FoundPoints中。GOTOStep 4;
Step 4:IF FoundPoints长度大于4 THENGOTOSTEP 5;
ELSE将数组传递给填充函数;GOTO STEP 3;
Step 5:对FoundPoints按点高程值进行插入排序。定义整形i=0,记录当前点在数组的位置GOTO Step 6;
Step 6:添加FoundPoints[i]到临时数组中,定义TempW记录其高程值。GOTOStep 7;
Step 7:定义j=i+1;IF FoundPoints[j].W!=TempW THENGOTOStep 17;ELSE GOTOStep 8;
Step 8:定义k=j+1;添加FoundPoints[k]到临时数组中;
IF FoundPoints[k].W==TempW THENGOTOStep 9;ELSE GOTOStep 8;
Step 9:将FoundPoints[k+1]放入临时数组传给填充函数;并将FoundPoints中k-3之后的所有元素放入NewFoundPoints;将这四个相同高程值的等值点记录在temp数组中录;定义flag=0,记录是否出现新的一对等值点。GOTOStep 10;
Step 10:将temp数组的元素加入临时数组中,定义m=4,记录当前点在NewFoundPoints的位置;GOTO Step 11;
Step 11:添加NewFoundPoints[m]到临时数组,定义TempW记其高程值。GOTOStep 12;
Step 12:定义n=m+1;IF NewFoundPoints[n].W== TempW

Step 13:flag=1;将临时数组传递给填充函数后清空。添加NewFoundPoints[n-1]到临时数组;m=n;GOTOStep 16;
Step 14:IF flag=0
THENGOTOStep15;
Step 15:将临时数组传递给填充函数后清空后添加temp数组的元素;GOTOStep16;
Step 16:IF NewFoundPoints[m]是最后一个元素
THEN将其添加对临时数组;传递给填充函数;退出程序;
ELSE GOTOStep 11;
Step 17:IF FoundPoints[i]是最后一个元素
THEN将其添加对临时数组;传递给填充函数;退出程序;
ELSE GOTOStep 6;
如图1的情况,排序后的点位AEHBDFGC,先后传递给绘图函数的点数组AEH、EFBDFG,FGC;如图2的情况,排序后点依次为AEJFGHIBDC(也可能是AEJFGHIDBC)。传递给填充函数的点依次为AEJ,EJFGHI然后进行特殊处理时传递给填充函数的点为FGHIB,FGHID,FGHIC。
2 实 例
笔者将算法应用油田含水饱和度等动态指标图中,网格数据比较平滑,在网格粗糙的情况下也具有较好的效果。如图3中等值带个数为5,网格密度分别为10*10和20*20以及网格密度为20*20等值带个数分别为10和20作为条件进行了测试,计算速度都很快。而且随着网格密度和等值带个数的增加,算法效果越好。
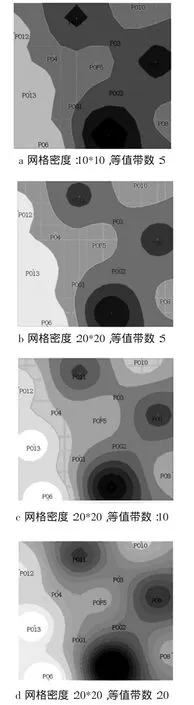
图3 算法效果Fig.3 Effects of algorithm
3 结 论
(1)提出了一种新的方法解决常规的绘制彩色填充等值带问题,该方法不需要在网格化数据的基础上进行等值线追踪,具有编程简单、计算量小的特点。
(2)本算法不需要讨论过多的种类,只需要特别处理具有相同权重的等值点为4的情况。
(3)本算法采用的四边形网格,但因为算法在寻找多边形时是按各点权重排序,而跟坐标无关。所以可以方便地推广三角形构网的等值带填充中。
(4)本算法已在程序系统中得到很好的应用,速度快,效果良好。
[1]徐胜利.一种堆栈式快速等值线图填充算法[J].计算机工程与应用,2010,46(8):193~195.
[2]吴自银,高金耀.一种基于格网的快速等值线充填算法[J].测绘学报,1999,28(4):350~354.
[3]张登荣,刘绍华,毛天露等.等值线自动建立拓扑关系算法与快速填充应用[J].中国图象图形学报,2001.6A(3):264~269.
[4]成建梅,陈崇希,孙红林.三角网格等值线自动生成方法及程序实现[J].水利学报,1998,29(10):23~26.
[5]庞世明,蔡玉华,靳文芳.等值线图的彩色填充方法[J].计算机应用,2004(1):60~62.
[6] Kantz H,Schreiber T.Nonlinear time series analysis[M].Beijing:Tsinghua UniversityPress,2000:42~47.
[7]郑宗汉,郑晓明.算法设计与分析[M].清华大学出版社.北京2010:278~285.
