GAP-TPE热分解动力学研究①

左海丽，肖乐勤，周伟良，徐复铭

(南京理工大学 化工学院，南京 210094)

0 引言

目前，国内外众多学者对GAP的在不同气氛、不同升温速率的热分解情况以及所遵循的机理进行了研究。如 Taker Satio等［1］研究了 GAP 在 Ar、N2和 O2气氛中，在低于标准大气压下，用CO2加热的热分解情况，指出热分解过程中表面温度变化分为3个阶段:熔解温度(493 K)、热分解开始温度(513 K)和表面最高温度(700～800 K)。陈智群等［2］用 Kissinger法得出GAP分解活化能为146.6 kJ/mol，用 Coats-Redfern法研究了GAP在反应深度4% ～37%的动力学参数，得出分解机理函数为g(α)= －ln(1－α)。刘畅［3］研究了GAP在空气和氮气中的热分解反应过程，并用得到GAP的热分解过程第一阶段的活化能为113.09～127.14 kJ/mol，所遵循的机理函数为 g(α)=(1 －α)－1－1。Haas等［4］通过 CO2激光诱导的方法，研究了GAP/IPDI/N-100在真空环境中分解产物，主要气体产物有 N2、CO、C2H4、HCN，可能还有 H2。Suresh等［5］对 TDI、IPDI和 MDCI固化 GAP 的热分解步骤进行了研究，认为固化GAP热分解分为2个阶段，第1个阶段为190～270℃;第2个阶段为270～450℃。Korobeinichev O P［6］研究了GAP样品的分解和燃烧化学，指出GAP的热分解在高加热速率下分3个加热过程完成。但关于GAP基含能热塑性弹性体(GAPTPE)的热分解的动力学研究鲜见报道。

本文用TG-DTG热分析手段，研究了GAP-TPE热分解的3个阶段，并得到了相关动力学参数。

1 实验

1.1 实验材料

4，4’-二苯基甲烷二异氰酸酯(MDI)，分析纯;聚叠氮缩水甘油醚(GAP)，相对分子质量3 000，羟值:33.58 mgKOH/g，试制品;一缩二乙二醇(DEG)，化学纯;乙酸乙酯，分析纯;丙酮，分析纯。

1.2 ETPE 的合成

将计量好的GAP于90℃下真空脱气3 h，然后充氮气进行保护，加入预热的MDI，在90℃反应2 h，降温至70℃，加入预热的DEG和一定量的溶剂快速搅拌，待体系达到一定粘度脱泡出料，在氮气保护下，30℃熟化18 h，90℃熟化3 d，得到GAP-TPE含能热塑型弹性体。其中，文中测试试样的—NCO/—OH摩尔比为0.98，硬段质量分数(即扩链剂与二异氰酸酯的质量占热塑性聚氨酯弹性体的质量百分数)为35%。

1.3 热重/微熵热重(TG/DTG)分析

热重/微熵热重(TG/DTG)分析在TGA/SDTA85/e型TGA仪上进行，样品质量(0.8±0.01)mg，测试气氛为氩气，氩气流速为30.0 ml/min，升温速率分别为5、20、30、40 K/min，温度范围为50 ～800 ℃。

2 结果与讨论

2.1 GAP-TPE的热分解过程

对升温速率分别为 5、20、30、40 K/min的 GAPTPE进行TG测试，其在氩气气氛中的热重(TG)及微熵热重(DTG)曲线如图1所示。

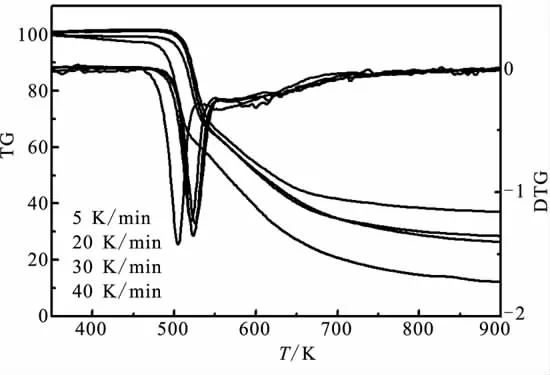
图1 不同升温速率下GAP-TPE的TG/DTG曲线Fig.1 TG/DTG curves of the thermal decomposition of GAP-TPE obtained at different heating rate

由图1可见，GAP-TPE的热分解分为3个阶段，预示整个热解过程是由3个阶段组成，这3个阶段不是完全分开，而是相互叠加的。因此，把实验DTG曲线分解成3个Gaussian峰，以20 K/min升温速率下的曲线图为例，3个Gaussian峰叠加的拟合曲线和实验DTG曲线完全重合，如图2所示。其中，第1阶段为叠氮基团分解，质量损失约25%;第2阶段为硬段氨基甲酸酯基的分解，质量损失约30%;第3阶段为软段长链高分子裂解成了小的链段，质量损失约16%。

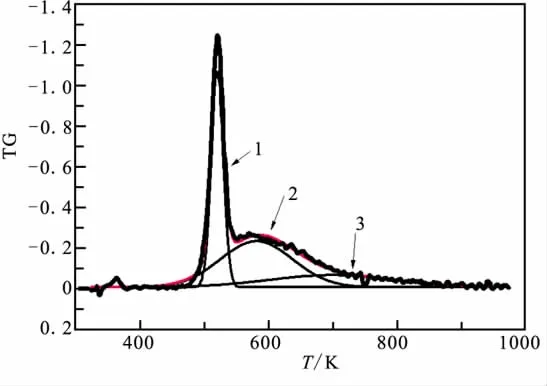
图2 20 K/min升温速率下GAP-TPE的微分失重曲线峰型分解结果Fig.2 Peak separation of differential mass loss curves of GAP-TPE obtained at 20 K/min

2.1.1 Kissinger法求GAP-TPE热分解动力学参数

根据不同升温速率下的DTG曲线的3个Gaussian峰的峰温数据见表 1，利用 Kissinger法［7］(式(1))将ln(β/Tp2)对1/T作图，由直线的斜率可求出GAP-TPE热分解3个阶段的反应活化能，截距可求出A，结果见表2。

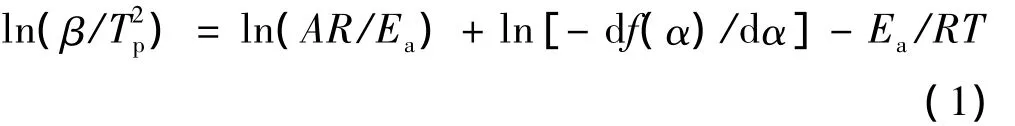
式中 β为升温速率;Tp为DTG曲线上的峰温;A为指前因子;R为气体普适常数，8.314 J/(K·mol);Ea为活化能;α为转化率(反应深度)。

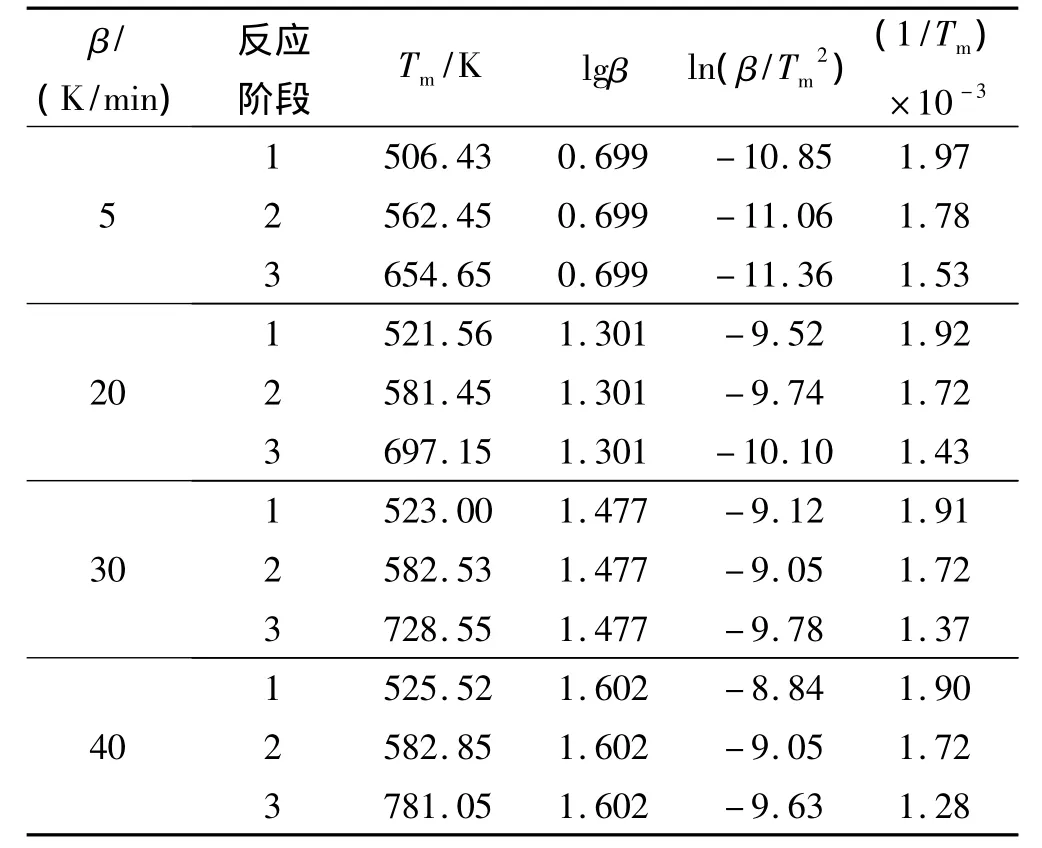
表1 图1中分解出各峰的特征量Table 1 Eigenvalues of each separated peak in Fig.1

由表2可知，GAP-TPE热分解3个阶段的活化能分别是223、235、57 kJ/mol。将第1阶段动力学参数Ea=223 kJ/mol、lnA=52.73 与文献［4］报道的GAP 在第1 阶段的 Ea=146.6 kJ/mol、lnA=28.89 结合，计算出两者的动力学温度［8］为112℃，说明所合成热塑性弹性体在低于该温度时有较高的稳定性。

表2 Kissinger和Ozawa法计算GAP-TPE各阶段的动力学参数Table 2 Kinetic parameters of each stage of GAP-TPE obtained by Kissinger and Ozawa method

2.1.2 Ozawa 法求反应活化能

Ozawa［7］法避开了反应机理来求取活化能，因而不会因反应机理而带来误差，常被用来检验其他方法求出的活化能值。假设在不同升温速率的峰温处，TG曲线都有相近的转化率(反应深度)。根据表1特征量，利用Ozawa法，将ln(β/Tp2)对1/T作图，由直线斜率可求出活化能，结果见表2。

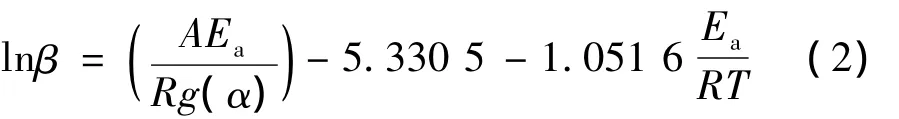
由表2可见，由Ozawa法求得的3个阶段的活化能分别是 222、232、65 kJ/mol，此结果与 Kissinger法求的基本一致。

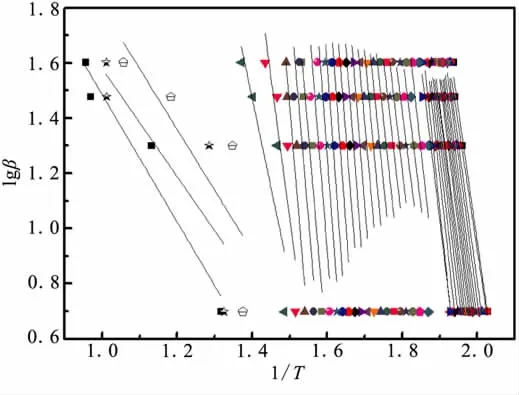
图3 GAP-TPE在不同反应深度(α=0.1～1)范围内lgβ-1/T 的曲线Fig.3 lgβ-1/T curvers of GAP-TPE at different conversion(α=0.1～1)

为了解整个GAP-TPE分解过程中活化能随反应深度的变化情况，用Ozawa法求解整个过程的活化能。图3为不同反应深度α=0.1～1范围内，lnβ-1/T的关系曲线，由直线斜率求的活化能随反应深度的变化情况见图4。由图4可见，GAP-TPE的活化能变化也存在3个阶段;第1阶段 α=0.2～0.42，平均活化能为205 kJ/mol;第2 阶段 α =0.42 ～0.64，平均活化能为235 kJ/mol;第3阶段 α=0.84～1，平均活化能为66.4 kJ/mol。由此可见，GAP-TPE的确存在3个阶段的热分解，其活化能值与用特征量求解的结果基本一致。

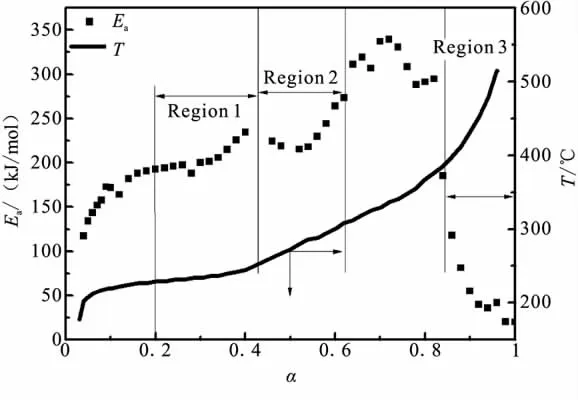
图4 活化能、温度随反应深度不同的变化情况Fig.4 Activation energy，reaction temperature with different changes of conversion

2.2 GAP-TPE热分解机理函数确定

对不同升温速率下GAP-TPE热失重的3个阶段，采用Coats-Redfern积分法［7］(式(3))来确定其遵循的反应方程。本文选用常见的9种机理函数(表3)对图1的热解失重数据进行计算，将结果进行线性回归处理，获得GAP-TPE热分解过程机理函数。

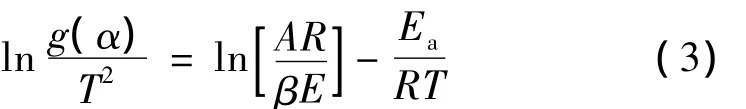
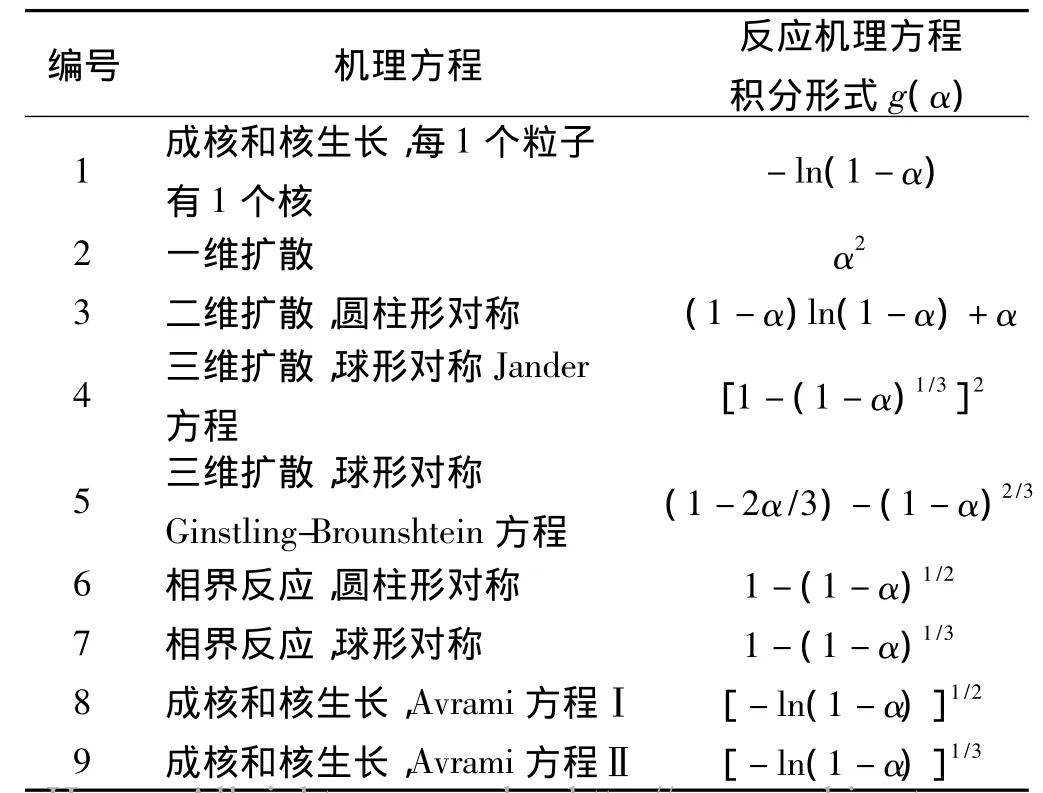
表3 常用热分解机理函数Table 3 Mechanism functions of the normal thermal decomposition

根据表3的9个机理函数类型，将相应的g(α)分别代入式(3)，以对1/T作图，得到9种机理方程的拟合曲线及得到的线性相关系数示于表4。

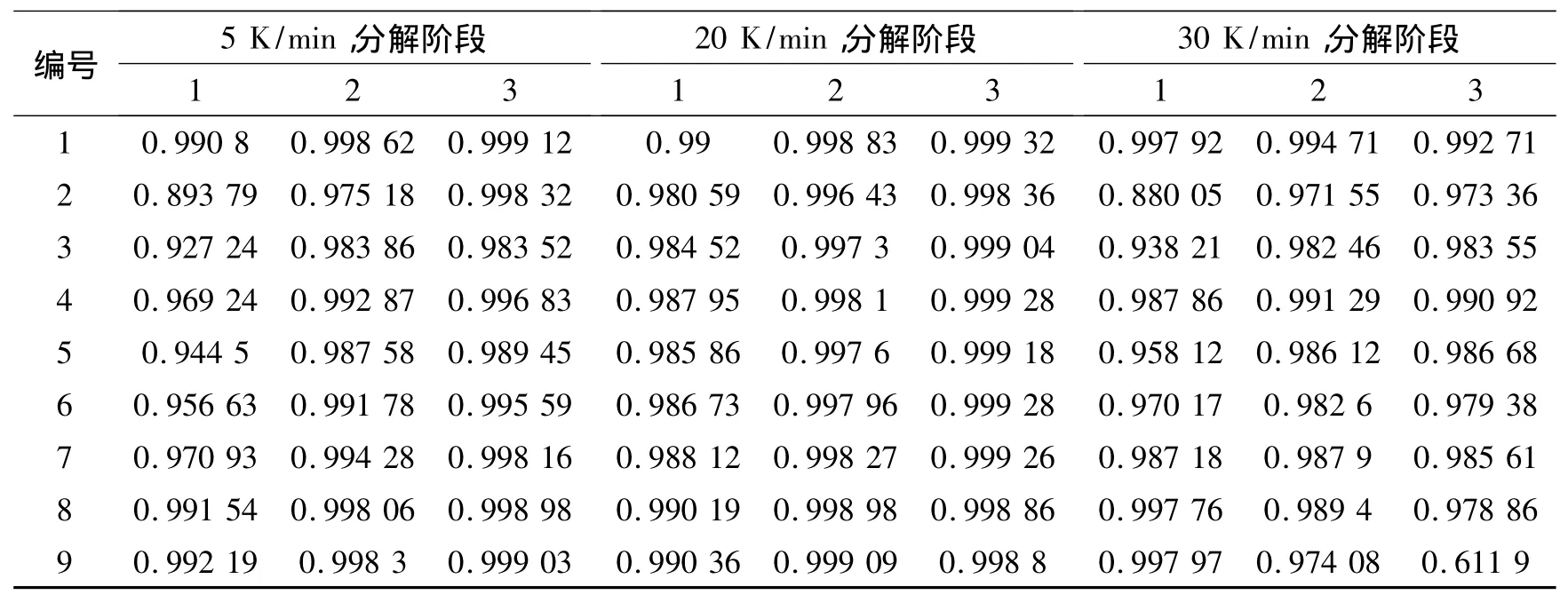
表4 各阶段GAP-TPE分解机理函数拟合直线线性关系Table 4 Linear fits of different decomposition mechanism function of GAP-TPE at different stages

由表4可见，GAP-TPE热分解的3阶段分别对应机理方程9、1和1具有良好的线性关系。由此得出，GAP-TPE热分解第1阶段合适的反应机理方程为随机核化Avrami方程Ⅱ，其对应的反应机理方程积分形式 g(α)=［－ln(1 － α)］1/3;第 2、3 阶段合适的机理方程都是成核和核生长，每1个粒子有1个核，对应的g(α)= －ln(1－α)。

3 结论

根据GAP-TPE热解DTG曲线的特点，把其热解过程分解成3个阶段，并用Kissinger法求得GAP-TPE热分解3个阶段的活化能分别是223、235、57 kJ/mol，lnA 分别是52.73、49.39、8.28。用 Ozawa 法求得活化能与Kissinger法基本一致。利用Coats-Redfern积分法求的3个阶段的机理函数分别为［－ln(1－α)］1/3、－ln(1－α)和－ln(1－α)。

［1］Takeo Saito，Masataka Shimodaa，Tsuyoshi Tsuyukib，et al.CO2laser-induced pulsating regression behavior of GAP at sub-atmospheric pressures［J］.Combustion and Flame，2001，124(4):611-623.

［2］陈智群，刘艳，刘子如，等.GAP热分解动力学和机理研究［J］.固体火箭技术，2003，26(4):52-54.

［3］刘畅.GAP热分解机理函数研究［J］.中国新技术新产品，2009:233-234.

［4］Haas Y，Ben Eliahu Y，Welner S.Infrared laser-induced decomposition of GAP［J］.Combustion and Flame，1994，96(3):212-220.

［5］Mathew S，Manu S K，Varghese T L.Thermomechanical and morphological characteristics of cross-linked GAP and GAPHTPB networks with different diisocyanates［J］.Propellants，Explosives，Pyrotechnics，2008，33(2):146-152.

［6］Korobeinichev O P，Kuibida L V，Volkov E N，Shmakov A G.Mass spectrometric study of combustion and thermal decomposition of GAP［J］.Combustion and Flame ，2002，129:136-150.

［7］刘子如.含能材料热分析［M］.北京:国防工业出版社，2008:11.

［8］刘子如，阴翠梅，刘艳，等.RDX和HMX的热分解Ⅱ——动力学参数和动力学补偿效应［J］.火炸药学报，2004，27(4):72-75，79.