冲压发动机加速阶段进气道内动态特性①

2011-03-13孙振华吴催生

固体火箭技术 2011年3期

孙振华，吴催生

(中国空空导弹研究院，洛阳 471009)

0 引言

目前，先进远程空射导弹多采用整体式冲压发动机作为动力装置，它采用双用途燃烧室，当助推器工作结束后，助推药柱燃烧完毕剩下的空间，即可作为冲压发动机的燃烧室，能大大提高导弹的容积利用率，但这样就必须在冲压发动机燃烧室的入口端安装密封堵盖，亦称为进气道出口堵盖。在导弹助推飞行阶段，进气道内通道被出口堵盖封闭，其流动涉及进气道的一些非稳定工作特性，对整体式固冲发动机的工作有非常重要的影响，有可能导致弹体或冲压发动机结构破坏。因此，对该阶段的动态特性进行研究显得十分必要。

目前，针对冲压发动机的动态特性研究多集中在冲压发动机的燃烧不稳定及进气道在超临界和亚临界状态下激波运动造成的非稳定工作研究，而对整体式冲压发动机助推加速过程动态特性研究很少。Fujiwar等［1］分析二维外压缩超声速进气道的激波振荡频率，与实验结果吻合，振荡频率同样随着质量流量的降低而增加。Nishizawa等［2］数值研究了自由流马赫数1.64 Ma时，外压式进气道在亚临界状态下的激波振荡现象。研究发现，在亚临界时振荡流动存在多个峰值频率。其中，低频成分来自亚音速扩压器的声学共振，高频成分是由来自楔面上的周期分离流动被吸除造成的，高频率成分在扩压器长度增大时消失。Lu P J等［3］数值分析了冲压发动机进气道喘振现象。结果表明，喘振来自进口处的局部流动不稳定以及气室中的声学振荡。刘占生等［4］采用数值模拟方法，研究了某超声速进气道结构的自激振荡现象，分析了振荡时进气道内流场的变化过程。研究表明，发生自激振荡时，进气道中流动产生大幅脉动，造成进气道壁板结构承受周期变化的气动载荷，载荷振荡频谱中包含多个特征频率，其与声模态频率相重合，表明自激振荡现象与声模态的相关性。Sivakumar等［5］采用非稳态的RANS方法，对二维冲压发动机进行了计算，获得了燃烧室内不同频率的压强振荡。周红梅、于胜春等［6－7］采用大涡模拟方法，分析了冲压发动机燃烧室内湍流涡的产生、发展、脱落与破碎过程，总结了导致压强振荡的有关因素，并分析了影响振荡频率和幅值的主要原因。秦飞等［8］采用大涡模拟耦合预混燃烧模型，分析了冲压发动机低频不稳定燃烧的成因。研究结果认为，漩涡运动耦合非稳态的燃烧热释放是激发燃烧室低频压强振荡的重要原因。李强等［9］采用大涡模拟方法，对串联式冲压发动机的助推段压强振荡进行了数值分析。研究表明，其属于整体模式的不稳定现象。

针对某整体式固冲发动机助推加速过程进气道内的动态特性，本文进行了数值仿真和相关风洞试验研究，分析了相同飞行高度下Ma变化对进气道内压强振荡特性的影响，可为整体式火箭冲压发动机的设计提供指导。

1 物理模型及计算方法

1.1 物理模型

冲压发动机的简化模型如图1所示。进气道为头部两侧进气方式，在进气道出口处装有堵盖，在整体式固体火箭冲压发动机处于助推阶段时，进气道堵盖处于关闭状态;助推结束后，通过转级指令将进气道出口处堵盖打开，来流空气通过进气道进入二次燃烧室，进而转换为冲压阶段。

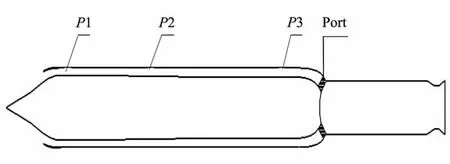
图1 冲压发动机简化模型示意图Fig.1 Schematic diagram of ramjet engine

1.2 数值方法

计算中，采用有限体积法求解雷诺平均后的三维N-S方程，紊流模型选用Jones和Launder提出的标准k-ε模型，并用一阶迎风格式离散。由于紊流模型只适用于离开壁面一定距离的紊流区域，而在与壁面相邻近的粘性边界层中，采用的是标准壁面函数修正，时间步长为1×10－4s。计算收敛准则为连续方程、动量方程、能量方程，以及k-ε方程的残差至少下降3个数量级，且监控点压强稳定。

本文的研究对象是对称体，流动也具有一定的对称性。在不考虑迎角和侧滑角组合的情况下，为减少计算量，选取飞行器周围的一半流动区域作为计算域，计算网格共约205万网格，网格质量满足单元内角＞15°，扭转角＜45°，正交性＞0.25。分别在进气道内和补燃室内设置监控点，检测出口堵盖打开前后的压强变化情况。

计算中，用到的边界条件类型有压力远场边界、压力出口边界、对称边界和无滑移绝热固壁等。

1.3 计算状态

根据不同的飞行状态，计算进气道出口堵盖打开前后的流场特性，计算状态如表1所示。

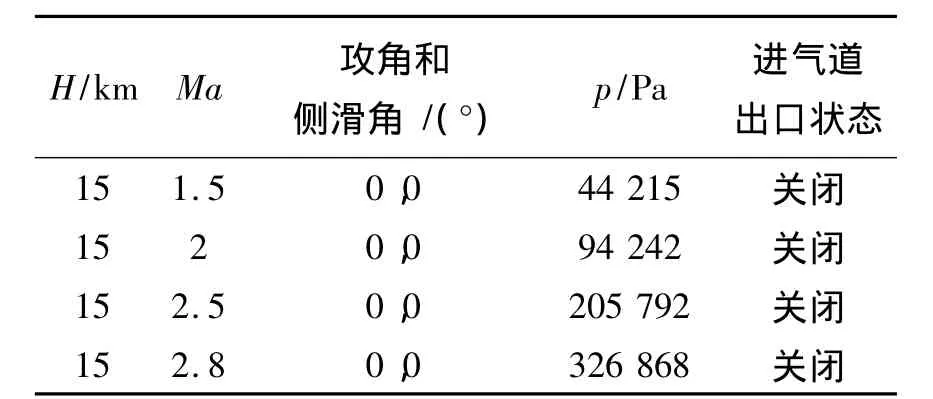
表1 计算状态Table 1 The calculation cases

2 计算结果与分析

数值计算的研究范围为Ma=1.5～2.8，主要针对固冲发动机助推加速过程中的典型飞行马赫数，可得到进气道出口堵盖打开前进气道内的振荡频率、幅度及其变化规律。

工况1进气道内监控点压强随时间的变化曲线如图2所示。

图2 工况1进气道内监控点压强随时间的变化曲线Fig.2 Time history of pressure oscillation on different inlet monitor points for case 1

从图2中可看出，各监控点压强随时间基本呈正弦规律变化，且进气道出口处监控点压强振荡曲线较平滑;各监控点振荡相位差较小，即某点压强处于峰值时，其余各点均接近峰值位置，进气道内各监控点振荡接近于整体振荡模式。分析认为，由于压强振荡是扰动传播引起的，各测点压强达到峰值点实际时间并非完全一致，但由于测点间距离较小，声速较大，因此各测点压强达到峰值时间相距很小，呈现出一种整体振荡模式。

另外，进气道沿程各监控点振幅变化不同，进气道入口附近振荡幅度较小，进气道出口附近振荡幅度较大。分析认为，当进气道堵盖没有打开时，进气道内通道形成了一个振荡系统，来流空气为其提供扰动源，堵盖作为压力波的反馈装置，在进气道内通道形成稳定的振荡。在进气道堵盖完全封闭的情况下，进气道整个亚音速通道形成一个扰动反馈装置，在亚音速通道内，其气流出现整体振荡的现象。由于存在气流进气道内部堆积和退出现象，在进气道入口附近，由于存在气流流动，其本身的压强是较低的;同时，流动过程使部分气流脉动得以损耗。因此，其振幅较进气道出口附近小。

值得注意的是仿真结果表明，进气道出口处监控点压强峰值超过来流总压。分析认为，对于进气道通道形成的振荡系统，由于自振是无阻尼的，来流的能量补偿了振荡系统自身的损耗，这种补偿是在整个振动周期内进行的，但在一个周期的不同阶段，有时能量补偿超过了系统自身损耗，有时相反，能量的补偿和损耗在一个周期内整体上得到平衡，这就造成了当能量补偿超过系统损耗时，监控点压强峰值会出现超过来流总压的情况。

工况2～4进气道内监控点压强随时间的变化曲线如图3～图5所示。

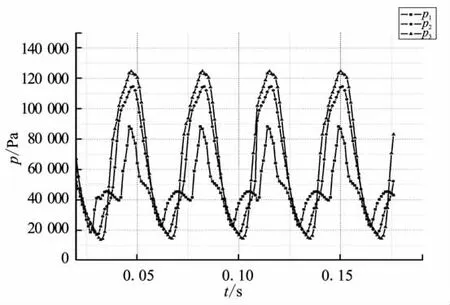
图3 工况2进气道内监控点压强随时间的变化曲线Fig.3 Time history of pressure oscillation on different inlet monitor points for case 2

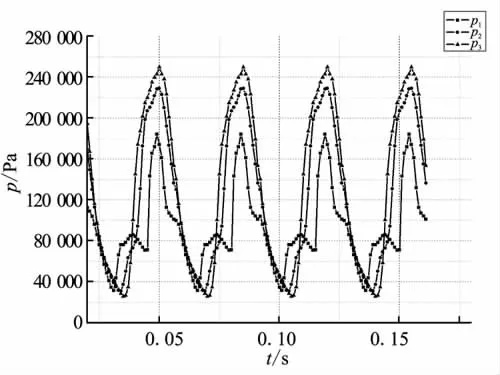
图4 工况3进气道内监控点压强随时间的变化曲线Fig.4 Time history of pressure oscillation on different inlet monitor points for case 3

图5 工况4进气道内监控点压强随时间的变化曲线Fig.5 Time history of pressure oscillation on different inlet monitor points for case 4

从图3～图5中可看出，其基本现象与工况1相似，监控点压强变化规律也与工况1一致，仅振荡频率和振幅与工况1稍有差别。这主要是由于对于不同的来流马赫数，即不同的能量输入，振荡系统的反馈速度和响应幅度不同。

图6为不同马赫数下各监控点压强相对振荡幅度计算值对比图。结果表明，各监控点的压强相对振荡幅度随马赫数增大而下降，进气道内不同位置处压强相对振荡幅度不同，越接近出口堵盖处，压强相对振荡幅度越大。

图6 不同马赫数下各监控点相对振荡幅度计算值Fig.6 Relative pressure oscillation amplitude on different inlet monitor points at different Mach numbers

3 试验验证及对比

为进一步准确地获得助推加速段进气道内的动态工作特性，本文开展了相关条件下的风洞试验，试验模型缩比2.25∶1，进气道内左右各布置了3路动态压强传感器，分别对应于计算监控点位置，检测其压强的实时变化过程。

试验数据的处理采用Danielson-Lanczos方法进行FFT变换，得到压力振荡的功率频谱，离散方法如式(1)所示，功率频谱计算如式(2)所示。

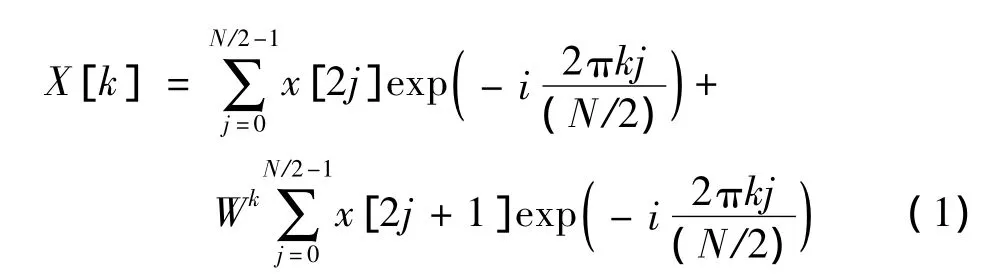
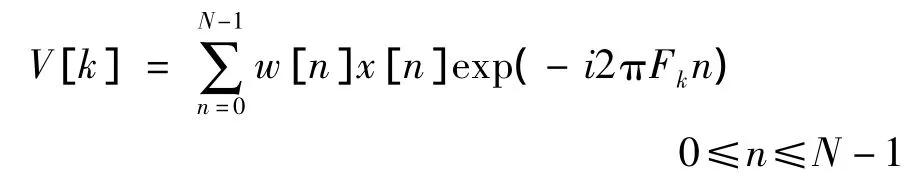
Ma=2.5状态流道沿程测点压强动态曲线与频谱特性如图7所示。从图7中可看出:(1)沿通道从前至后，各测点平均压强依次增大;(2)各测点频率特性一致，沿通道从前至后，振幅依次增大;(3)在一阶频率处能量较大，其余高阶频率能量低一个量级以上，在实际工程中，可不用考虑其影响;(4)测点3、6的压强峰值超过来流总压，这些现象与上述仿真过程中得到的结果吻合较好。

图7 各测压点压强动态曲线及频谱特性图Fig.7 Pressure evolution and spectrum characteristics at different measuring points

图8为Ma=2.5状态下不同测点的动态压强测试曲线。从图8中可看出，进气道出口堵盖打开前，进气道通道内压强振荡基本属于整体模式的不稳定振荡。

图9为风洞试验中不同马赫数下进气道压强相对振荡幅度对比。结果表明，各测点压强相对来流总压的振荡幅度随马赫数增大而下降。进气道入口附近，压强振荡相对幅度较小;进气道出口附近，相对振荡幅度较大。以上规律与仿真结果一致。

图8 Ma=2.5风洞试验不同测点动态压强变化Fig.8 Temporal variation of pressure at different measuring points for Ma=2.5 wind test

图9 不同马赫数下进气道压强相对振荡幅度试验值Fig.9 Relative pressure oscillation amplitude at different Machs numbers for wind tests

根据相似理论，对试验数据进行换算处理，得到真实进气道通道状态内振荡频率值，其随来流马赫数变化规律如图10所示。从图10中可看出，压强振荡频率随马赫数增大略有升高。分析认为，随马赫数增大，进气道通道入口温度升高。根据声学共振原理，当地声速越大，因此共振频率越高。另外，仿真值与风洞吹风试验处理值规律较为一致。