寒区土壤源热泵换热埋管的水热力耦合分析

郑 平,吴 明,赵 玲

(辽宁石油化工大学a.石油天然气工程学院;b.职业技术学院,辽宁抚顺 113001)

寒区土壤源热泵换热埋管的水热力耦合分析

郑 平a,吴 明a,赵 玲b

(辽宁石油化工大学a.石油天然气工程学院;b.职业技术学院,辽宁抚顺 113001)

为解决寒区土壤源热泵地下埋管冻胀安全性问题,根据传热学、渗流和冻土力学理论建立寒区土壤源热泵水热力耦合的数学力学模型及其控制方程。利用FEPG有限元自动生成软件,对大庆油田某土壤源热泵地下埋管所在土体内温度场分布、冻胀位移及应力作用进行仿真计算,并对不同深度、不同回填区土壤导热系数、不同管脚间距情况进行了对比分析。结果表明,土壤源热泵运行初期,土壤未冻结,埋管的位移量很小。土壤温度达到相变温度后,土体冻结体积增大,埋管发生挤压变形。当土壤温度超过冻结相变区(-0.75℃,-0.30℃)时,埋管不会发生连续不断的变形。关键词：寒区;土壤源热泵;换热埋管;相变温度场;位移场;应力场;耦合;冻胀安全

地源热泵系统是利用蕴藏于大地内的大量低品位能量为建筑物供热空调提供冷热源的新颖的空调设备[1]。地源热泵系统的显著特征就是用地下埋管换热器回收土壤热源。在寒区冬季供暖条件下,在土壤源热泵埋管换热器入口,液体的温度一般低于0℃,换热器周围含有水分的土壤有可能冻结。土壤的冻结会使地下换热埋管发生挤压和不规则变形,导致损坏地下埋管,对土壤源热泵换热埋管的安全性造成严重影响。在将冻土力学理论应用于寒区工程领域的研究中,国内外学者已取得了一些成果[2-7]。于明志等[8]分析了土壤冻结对土壤源热泵中换热器与周围土壤热交换过程的影响,探讨了土壤初始温度、土壤水分、斯蒂芬数等因素与冻结锋面发展和土壤温度分布的变化关系。但在寒区土壤源热泵埋管的安全运行领域,应用冻土力学理论的研究并不多见。

寒区冻结土壤与非冻结土壤存在很大不同之处,主要表现在冻结土壤中存在着温度场、水分场和外荷载的强耦合作用。以往的研究中,由于U型埋管地下换热器的几何形状和土壤传热的复杂性,在建立土壤源热泵换热埋管模型时,通常忽略了冻土中的水分迁移,不考虑水分和相变潜热对温度场的影响[9-11]。本文在传热、渗流和冻土力学理论基础上,建立了带相变的三维温度场、水分场和应力应变场耦合问题的数学模型和控制方程。在计算埋管地下换热器周围土壤温度场时,考虑冻土内水分迁移和冰水相变的影响,运用有限单元法,对寒区土壤源热泵换热埋管进行了热力强度和安全性方面的分析。

1 寒区土壤源热泵三维耦合数学模型

土壤源热泵地下换热埋管的结构如图1所示。竖直U型管安放在竖井中,竖井中填有回填土。U型管中的流体通过管壁、回填土和周围的土壤换热。流体在U型管中流动,构成闭式循环回路。

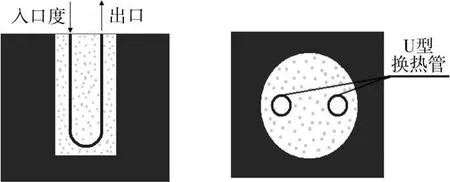
图1 地下换热埋管图

1.1 基本假设

1)U型埋管内液体的流速均匀一致(忽略重力项对流速的影响)。

2)土壤的导热系数、孔隙率、比热、密度等物性参数在同一水平面上是均匀一致的,仅沿轴向(深度)方向上发生变化。

3)忽略U型管管壁与回填材料、回填材料与土壤之间的接触热阻。

4)因为端部弯管和整个竖直管道与土壤换热来说是小量,故仅考虑竖直管道与土壤的换热,忽略U型管末端弯管与土壤换热的部分。

1.2 数学模型

1.2.1 三维传热控制方程[12]：

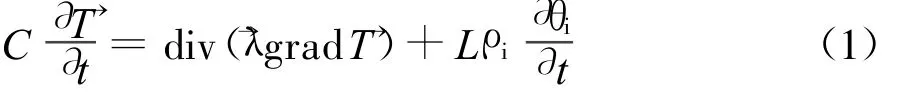
式中：λ为土壤的导热系数,C为土壤容积热容量,T为土壤任意时刻的温度,L为土壤相变潜热,ρi为冰的密度,θi为土壤体积含冰量。

1.2.2 水分迁移方程

式中：ρw为水的密度,θw为土壤液相水体积含量,K为土壤水分扩散系数,t为运行时间。

1.2.3 联系方程

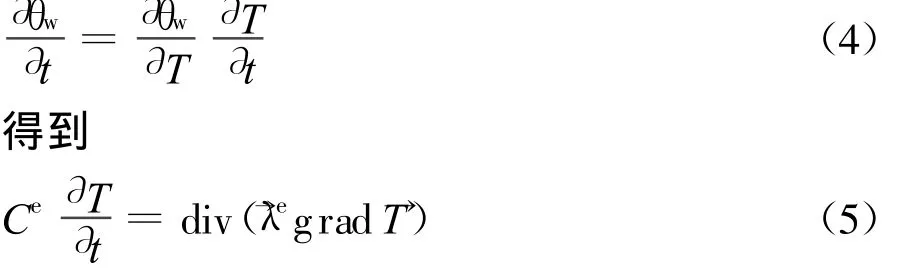
式中→λe和Ce分别为土壤的等效导热系数和等效容积热容量,其值分别为

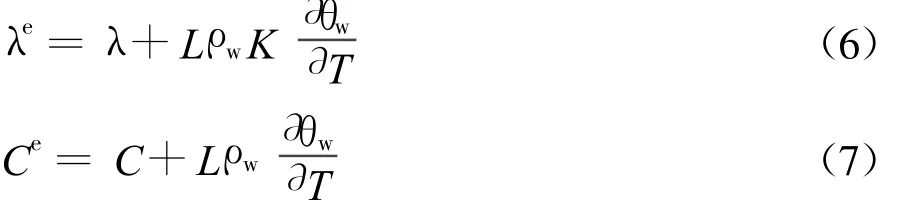
由于土壤的冻结相变主要发生在剧烈相变区,而不是严格地发生在某一特定的情况,因此可以把相变潜热看作小温度范围内的大热容。这样就能把分区描述的控制微分方程(1)-(5)方程简化,成为整个求解区域上合适的非线性热传导方程。根据显热容方法,求解区域内的λ、C和K分别为[13]：

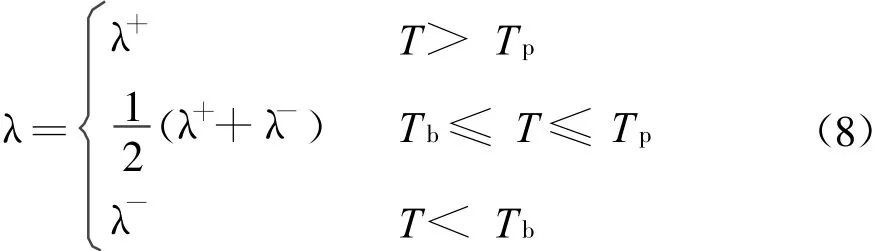
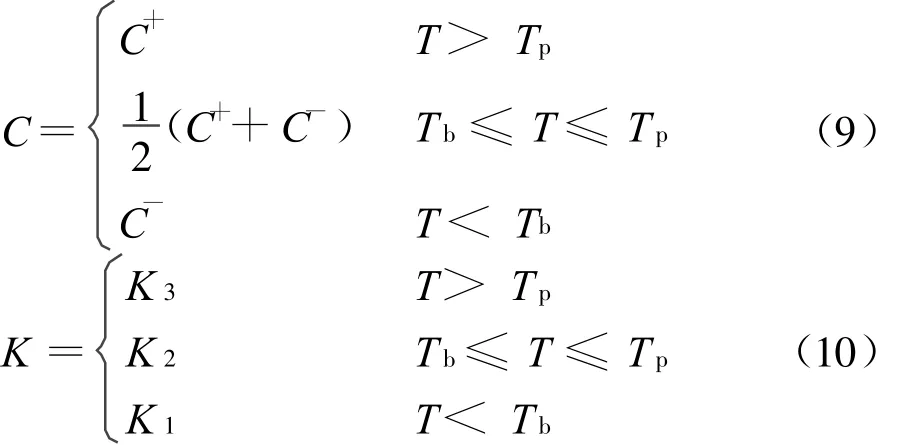
式(1)、(2)、(3)方程加上一定的初始条件和边界条件,构成了寒区土壤源热泵冰水相变和水分迁移问题的计算模型。

这种热传导问题,其控制方程(4)中的热参数很大程度上取决于温度,冻融两相界面随时间变化,在此界面上热量被吸收和放出,并产生巨大的相变潜热。因此在数值计算上,这类问题是一种大空间尺度、大时间的非线性问题,解的叠加思路不能成立。但模型可以在一定条件下进行简化。如果土壤源热泵在冬季供暖工况下运行,土壤中不考虑含水和含冰的具体数量,而只考虑两者对U型换热埋管温度场变化的影响,就可以不同时求解温度场和水分场,只求解方程式(5)-(7)即可[14]。

上述方程,再加上应力应变场和边界条件、初始条件方程,就可以进行土壤源热泵周围冻土的水、热、力三场三维空间的耦合计算,求出温度、水分、应力、位移等参数。

因为冻土的热胀冷缩量非常小,如果只考虑土体冻结后水结冰体积增大而产生的膨胀,体积膨胀量约为9%[15]。假设条件：土体为饱和黏土,孔隙比为99%,且水分填满全部孔隙,1单位体积土体内,有0.49单位体积的水分。则土体冻结后的体积膨胀量为

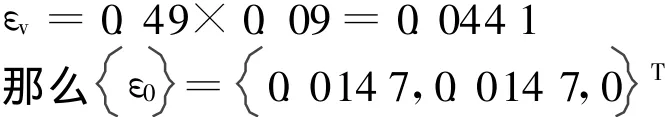
方程(5)-(17)即构成了土壤源热泵换热埋管含冰水相变的温度、水分、应力三场的耦合方程组。

2 定解条件

由于U型管两只管脚之间的传热条件不对称,但两管脚中心线所构成的平面两侧无论是几何形状还是传热、流动过程均是对称的,故简化的物理模型见图2。由于竖井半径远远小于井深,属于细长型几何体,考虑温度在井深轴向相对径向变化较小,在用有限单元法划分网格时,沿井深方向网格划分不易过密。同时,由于管壁及钻孔回填材料相对钻孔外土壤温度梯度较大,因此,对U型换热埋管旁回填材料用三角形单元进行加密划分,而钻孔外土壤采用三角形单元划分,确保准确捕捉到温度的变化,网格划分见图3。

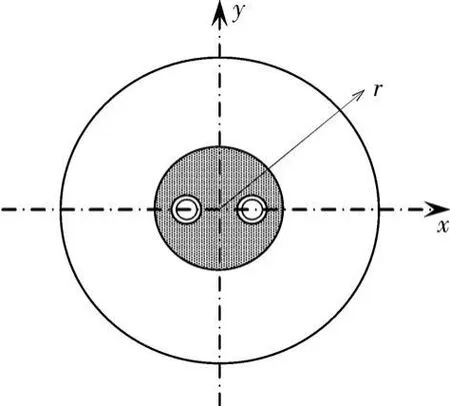
图2 简化物理模型

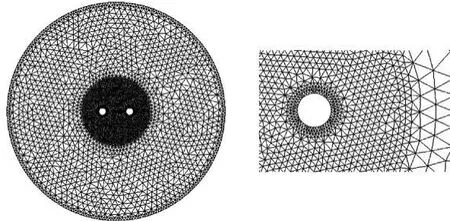
图3 计算区域网格划分及局部放大图

2.1 边界条件

1)温度边界条件。文中研究大庆地区冬季供暖工况土壤源热泵换热埋管问题,选取大庆冬季地面平均温度为-5℃。

埋管外壁r=r0,当热泵运行时,

式中：q为单位管长换热量。当热泵停止时,

钻孔外土壤外边界为绝热条件,即

2)位移边界条件。文中研究埋管在x和y方向的挤压变形,因此限制钻孔外壁土壤外边界 x方向和y方向,管壁进出口边界的x方向和y方向自由。

3)应力边界条件。埋管及钻孔内外边界上均无载荷作用。

2.2 初始条件

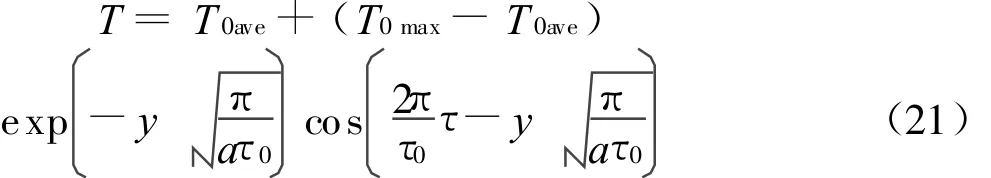
2.3 参数选取

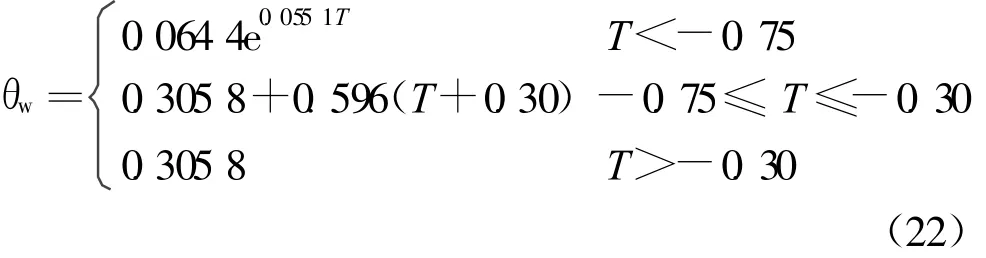
3 计算结果分析

文中研究土壤源热泵在寒区冬季运行时,钻孔内不同回填材料、不同管脚间距、不同深度下土体温度场的分布,以及在冻融过程中水分冻结、土体膨胀对地下埋管挤压产生的影响。埋管在钻孔内对称均匀布置,管内流体出口温度为-5℃,尺寸为Φ32×3 mm,埋管深度为10m,双管间距100 mm,回填区半径120mm,模拟区域半径0.5m,单位管长的换热量为50W/m。

图4为土壤源热泵运行500 h和2 000 h靠近地面处,埋管周围土壤的温度分布。

图4 土壤源热泵运行50 h,2 000 h后土壤温度分布

图5土壤源热泵运行2 000 h,在竖井5m和10 m深度处埋管周围土壤的温度分布。

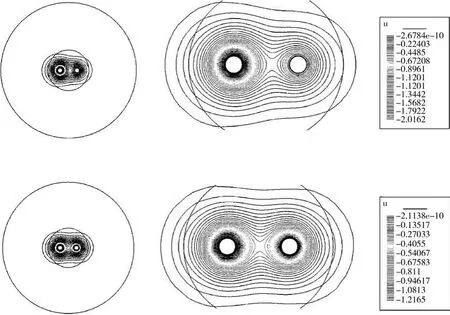
图5 土壤源热泵运行2 000 h后竖井5m和10 m土壤温度分布

图6为土壤源热泵运行2 000 h,采用3种不同导热系数的回填土材料,靠近地面处埋管(-0.12, 0),(-0.066,0)间土壤温度随x轴变化曲线。设原来回填土材料的导热系数为λ1,新回填土材料的导热系数为λ2和λ3。回填土材料导热系数值见表1。

表1 回填土材料导热系数值

图6 (-0.12,0),(-0.066,0)间土壤温度随x轴变化曲线

图7为不同导数系数回填土材料下,埋管入口管壁中心点(0,-0.064)在2 500 h内x方向位移图。

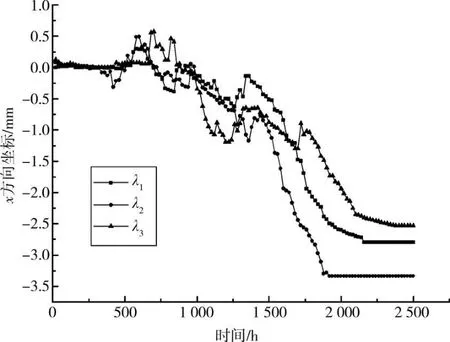
图7 埋管入口管壁中心点(0,-0.064)在2 500 h内x方向位移图

图8为回填土土壤导热系数λ1,地源热泵运行2 000 h后,土壤冻结膨胀对埋管形成的x方向挤压变形图。图中黑色图形为原来U形埋管形状,红色图形为变形后U形埋管形状。

图9为不同管脚间距下,靠近地面回填土边界点(-0.12,0)在2 000 h内的温度分布。

图10为不同管脚间距时埋管入口管壁中心点在2 500 h内x方向位移图。

由图4可看出,在土壤源热泵运行期间,靠近管壁的土壤温度变化比较剧烈。运行50 h后,土壤最低温度由初始时刻的0℃下降到-3.051℃,2 000 h后达到-3.362 7℃。随着运行时间的增长,土壤最低温度逐渐降低,热影响区域逐渐增大。

由图5可看出,在竖井5 m和10m深度处的土壤温度场是有差别的。因为初始条件中设定了土壤随深度变化这一情况,土壤深度大,土壤温度初始值高;同时流体从埋管入口流到出口的过程中,流体自身有温降,与管壁和土壤之间还有热量的传递,因此靠近埋管入口和出口的土壤温度均不同,在竖井5 m深度处,埋管入口土壤最低温度为-2.016 2℃,竖井10 m深度处,埋管入口土壤最低温度为-1.216℃,符合工程实际。

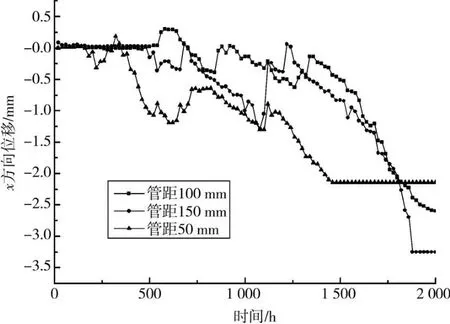
图8 土壤冻结膨胀对埋管形成的挤压变形

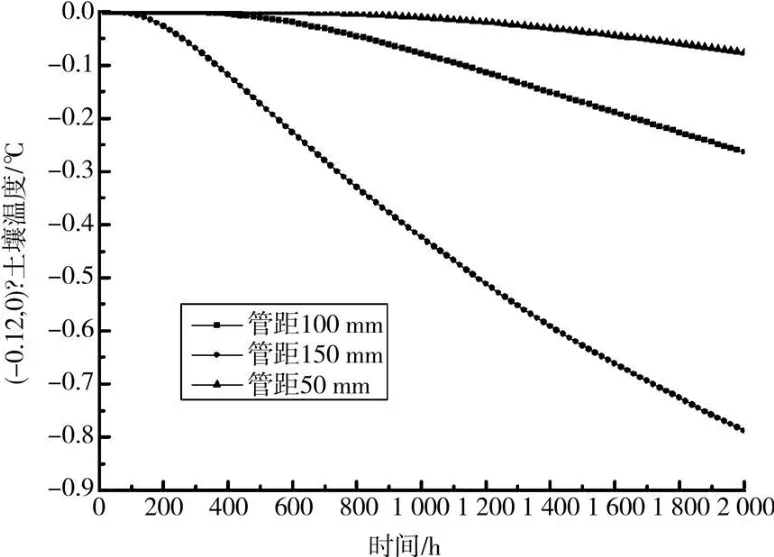
9不同管脚间距下靠近地面处回填土边界土壤点(-0.12,0)在2 000 h内的温度分布

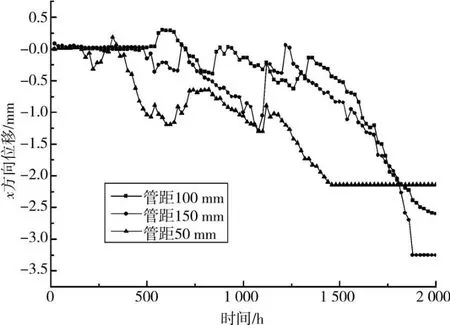
图10 不同管脚间距时埋管入口管壁中心点在2 000 h内x方向位移图

由图6可看出,回填区土壤导热系数相对较大的材料土壤温降快,并且靠近埋管处温降变化最大,距离埋管越远,温降变化越不明显。结合监测的出口水温可知,回填导热系数相对较大的材料,在运行相同的时间内水温升高较快但不稳定,导热系数大的材料对两管间热量的干扰较大。但监测水温和数据模拟说明,采用导热系数较大的回填材料有利于提高换热器的换热效果。

由图7可看出,以回填土土壤导热系数λ1为例,在土壤源热泵运行前560 h,土壤内水分未冻结,土壤温度未到相变温度。土壤内埋管发生的位移量很小,可以近似为零。运行1 500～2 200 h后,靠近管壁的土壤温度接近相变温度,水分冻结后土体的体积急速增大,膨胀位移应变产生的应力超过了管壁的抗压强度,对地下埋管造成剧烈的挤压,进而产生很大的变形。在560～1 500 h之间,埋管的位移情况不很稳定。在2 260～2 500 h之间,埋管管壁位移发生量趋于平稳,最大位移量为2.8mm。这是由于土壤体积增大现象只发生在冻结相变区(-0.75℃,-0.30℃)。即使温度持续下降,埋管管壁也不会发生连续不断的变形,位移量会保持基本恒定不变,土壤冻结程度随时间的变化很小。

回填区不同导数的土壤,埋管管壁发生不同的位移情况。当土壤导热系数为λ2时,埋管运行340 h后土壤最先到达相变温度,在2 000 h后埋管管壁位移量趋于平稳,最大位移量为3.5 mm;当土壤导热系数为λ3时,埋管运行680 h后土壤最先到达相变温度,在2 380 h后埋管管壁位移量趋于平稳,最大位移量为2.53 mm。

Lenarduzzi等[17]对土壤冻结膨胀对地下埋管造成的挤压情况进行了研究和分析。现场实际数据说明,由于管道被冻结土壤挤压,情况严重时管径会从原来的32 mm减小到19 mm。由于管径变小造成的节流作用,流体流量约减少50%,对热泵热量输出产生严重影响,地源热泵的供热性能系数COP也会随之降低。

由图9可以看出,当管脚间距为150 mm时,靠近地面回填土边界点(-0.12,0)土壤温降最大,为-0.78℃;管脚间距为100 mm时,温降次之,为-0.26℃;管脚间距为50 mm时,温降最小,仅为-0.077℃。此结果说明在其他条件不变的情况下,适当增加管脚间距会提高埋地换热器的换热量,但这会因此增加初投资费用。管脚间距不能设置过小,2个管之间会出现相互换热的情况,即“热短路”现象[18],会降低地下埋管换热性能。

由图7、10可看出,当管脚间距为100 mm时,埋管入口管壁中心点在接近560 h后发生变形,最后在2 260 h后位移量逐渐趋于平稳,最大位移量为2.8 mm;当管脚间距为150 mm时,因为管脚间距最大,埋管入口管壁周围土壤温度最迟达到土壤中水分相变温度,因此管壁中心点在接近500 h后发生变形,最后在1 880 h后位移量逐渐趋于平稳,最大位移量为3.254mm;当管脚间距为50 mm时,因为管脚间距最小,埋管入口管壁周围土壤温度最快达到土壤中水分相变温度,因此管壁中心点在接近400 h后发生变形,最后在1 460 h后位移量逐渐趋于平稳,最大位移量为2.14 mm。

图11为为回填土土壤导热系数λ1,地源热泵在运行2 000 h后,地下埋管x方向应力变化图。

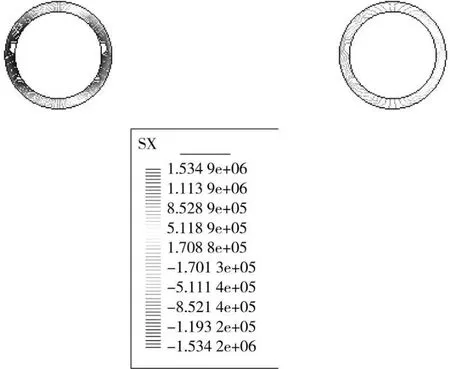
图11 运行2 000 h后埋管x方向应力变化图

从图11看出,U形埋管应力最大承受部位是入口管水平方向的两点,此处正是埋管挤压变形最严重的部位,所受应力约为1.5 MPa。在实际工程设计中,聚乙烯管的最终变形量应按照所选管材的实际强度来确定。当变形严重或大于容许变形时,必须合理选择强度较高的材料,或者适当采取防治冻胀措施,来减轻冻胀的危害。

4 结 语

1)土壤源热泵运行期间,靠近管壁的土壤温度变化比较剧烈。随着运行时间的增长,土壤最低温度逐渐降低,热影响区域逐渐增大。

2)土壤温度场随竖井深度增大,最低温度逐渐减小;随管脚间距的增大,土壤温降逐渐增大。适当增加管脚间距会提高埋地换热器的换热量,但这会因此增加初投资费用。管脚间距不能设置过小,两个管之间会出现相互换热的情况,即“热短路”现象,会降低地下埋管换热性能。

3)土壤的冻结会使地下换热埋管发生挤压和不规则变形,导致损坏地下埋管,对土壤源热泵换热埋管的安全性造成严重影响。

4)回填区土壤导热系数相对较大的材料土壤温降快,采用导热系数较大的回填材料有利于提高换热器的换热效果。同时,回填区土壤导热系数越大,埋管周围土壤中水分在越短时间内到达相变温度,埋管管壁水平位移量越快趋于平稳,最大位移量越大。因此在实际工程应用中,应当综合考虑回填区土壤的导热系数的选择,防止寒区土壤源热泵发生较大的冻胀破坏。

5)管脚间距越小,埋管周围土壤中水分在越短时间内到达相变温度,埋管管壁位移量越快趋于平稳,但最大位移量越小。因此,在实际工程应用中,除了“热短路”的换热影响外,还应考虑间距对埋管冻胀的影响,管脚间距不能过小。

6)在实际工程设计中,聚乙烯管的最终变形量应按照所选管材的实际强度来确定。当变形严重或大于容许变形时,必须合理选择强度较高的材料,或者适当采取防治冻胀措施,来减轻冻胀的危害。

[1]YU MZ,DIAO N R,FANG Z H.A pilot p rojectof the closed-loop ground-source heat pump system in China [C]//Proceeding of 7 IEA Conferences on Heat Pumping Techno logies.Beijing：China A rchitectureand Building Press,2002：356-364.

[2]KLEIN J.Finite element method for time-dependent problem s of frozen soils[J].International Journal for Numerical and Analytical Methods in Geomechanics, 1981,5：263-283.

[3]RA IMAND,ROEGIERS JC.Fluid flow and heat flow in deformab le fractured porousmedia[J].International Journalof Engineering Science,1994,32：1615-1633.

[4]KOUI K IM,WEI ZHOU,SCOTT L.Frost heave redictions of buried chilled gas pipelinesw ith the effect of permafrost[J].Co ld Regions Science and Techno logy,2008,53(3)：382-396.

[5]LA I YUANMING,WU HUI,HU YUANLIN. Analytical viscoelastic solution for frost force in coldregion tunnels[J].Co ld Regions Science and Techno logy,2000,31(3)：227-234.

[6]李洪升,刘增利,梁承姬.冻土水热力耦合作用的数学模型及数值模拟[J].力学学报,2001,33(5)：621-629.

LIHONG-SHENG,LIU ZENG-LI,LIANG CHENGJI.Mathematicalmodel for coup led moisture,heat and stress field and numerical simu lation of frozen soil[J]. A cta Mechanica Sinica,2001,33(5)：621-629.

[7]MA WEI,CHENG GUODONG,WU QINGBA I. Construction on permafrost foundations： Lessons learned from the Qinghai-tibet railroad[J].Cold Regions Science and Techno logy,2009,59(1)：3-11.

[8]于明志,方肇洪,李明钧.土壤冻结对地热换热器传热的影响[J].山东建筑工程学院学报,2001,16(1)：42-46

YU MING-ZHI,FANG ZHAO-HONG,LI MINGJUN.The influence of soil freezing on theheat transfer betw een heat exchanger of ground-source heat pumps and its ambient[J].Journal of Shandong Institute of A rchitecture and Engineering,2001,16(1)：42-46

[9]任晓红,孙纯武,胡彦辉.U型埋管换热器三维数值模拟和供热实验研究[J].重庆建筑大学学报,2004,26 (5)：90-95.

REN XIAO-HONG,SUN CHUN-WU,HU YAH-HUI. A three-dimensional numerical model and experimental research for U-tube ground heat exchanger in heating operation[J].Journal of Chonqing Jianzhu University, 2004,26(5)：90-95.

[10]宋小飞,温治,司俊龙.地源热泵U型管地下换热器的CFD数值模拟[J].北京科技大学学报,2007,29(3)：329-333.

SONG XIAO-FEI,W EN ZH I,SI JUN-LONG.CFD numerical simu lation of a U-tube ground heat exchanger used in ground source heat pumps[J].Journal of University of Scienceand Technology Beijing,2007,29 (3)：329-333.

[11]陈友明,王宇航,莫志娇,等.竖直U型埋管地下换热器的传热模型[J].太阳能学报,2008,29(10)：1211-1217.

CH EN YOU-MING,WANG YU-HANG,MO ZH IJIAO,et al.Heat transfer model of vertical U-tube underground heat exchanger[J].Acta Energiae Solaris Sinica,2008,29(10)：1211-1217.

[12]吴紫汪.马巍冻土的强度与蠕变[M].兰州：兰州大学出版社,1994：48-50.

[13]梁承姬,李洪生.输冷管道附近土体冻结过程的水热力耦合数值模拟[J].上海海运学院学报,2000,21(4)：85-91.

LIANGCHENG-JI,LIHONG-SHENG.Numerical analysis for coupled of moisture heat and stress fields during soil freezing around the buried chilled pipeline[J].Journal of ShanghaiMaritime University,2000,21(4)：85-91.

[14]朱志武,宁建国,马巍.土体冻融过程中水、热、力三场耦合本构问题及数值分析[J].工程力学,2007,24(5)：138-144.

ZHU ZHI-WU,NING JIAN-GUO,MA WEI.Constitutive model and numerical analysis for the coupled problem ofwater, temperatureand stress fields in the process of soil freeze-thaw [J].Engineering Mechanics,2007,24(5)：138-144.

[15]李南生,谢利辉,陈薛浩.寒区浅埋输油管线冻胀安全性分析[J].结构工程师,2008,24(1)：35-40.

LI NAN-SHENG,XIE LI-HU I,CHEN XUE-HAO. Frozen-heaving of frost-soil bed of shallow buried oil pipeline in co ld region[J].Struc tural Engineers,2008, 24(1)：35-40.

[16]安维东,吴紫汪,马巍,等.冻土的温度、水分应力及其相互作用[M].兰州：兰州大学出版社,1989：184-211.

[17]FJLENARDUZZI,CBH CRAGG,H SRADHKRISHNA. The importance of grouting to enhance the performance of earth energy systems[J].Ashrae Transaction,2000,106(1)：424-434.

[18]赵军,张春雷,李新国,等.U型管埋地换热器三维传热模型及实验对比分析[J].太阳能学报,2006,27(1)：63-66.

ZHAO JUN,ZHANG CHUN-LEI,LIXIN-GUO,et al. Three-dimensional heat transfer model and experimental analysis of U-pipe heat exchanger[J].A cta Energiae Solaris Sinica,2006,27(1)：63-66.

(编辑 王秀玲)

Thermal Dynam ic Analysis of Buried Hent Exchanger in Ground-source Heat Pum p System in Cold Region

ZHENGPinga,WUMinga,ZHAOLingb

(a.College of Petro leum Engineering;b.Vocational Technical College, Liaoning Shihua University,Fushun 113001,Liaoning,P.R.China)

In order to solve the frost-heaving safety problem s of buried heat exchanger hydronic in groundsource heat pum p,a mathematics mode1 and its contro1 equation w ere put forw ard according to heat transfer,filtration theory and mechanics of frozen soil,which is the coup lings problem of temperature field,hydronic field and stress field.The temperature field,frost heaving displacement and stress distribution of ground-source heatpump in Daqing oilfield were simulated w ith finiteelementsmethod.The contrast and analyses are carried out according to the different soil depth,the different soil thermal conductivity in backfilled areas,the different spacing of tube foot.The results showed that the least temperature and heat affected zone in soil increases gradually w ith operating time.A t the beginning of operation,the displacement of buried heatexchanger is smallbecause the soil is not frozen.When the soil temperature reaches the phase tem perature,soil vo lume increases in size,and then buried tube deform s. When soil temperature exceeds between-0.75℃and-0.30℃,buried tube doesn't deform.

cold region;ground-source heat pum p;heat exchange buried tube;phase change temperature field;displacement field;stress field;couplings;frozen-heaving safety

TK 512

A

1674-4764(2011)03-0100-07

2010-12-18

中国石油天然气股份公司资助项目(200703-04)

郑 平(1973-),女,副教授,博士生,主要从事土壤多场耦合问题研究,(E-mail)zhengping0413@163.com。

吴 明(通讯作者),男,教授,博士,主要从事土壤多场耦合问题研究,(E-mail)wum ing0413@163.com。