计及空腔能量耗散的尖劈结构声学特性研究

计 方 姚熊亮

哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

计及空腔能量耗散的尖劈结构声学特性研究

计 方 姚熊亮

哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

以喇叭型空腔为例分析了声波在尖劈空腔中的传播规律，给出了计及空腔能量耗散作用的尖劈结构吸声系数计算方法，通过声管测试验证了本文算法的有效性。在此基础上，通过数值试验预报了声呐平台区振动及自噪声分布，对比分析了空腔尖劈敷设方案对其声学特性的影响。结果表明：空腔对较低频段声波能量吸收有很大作用，在3 kHz以下频段计算空腔尖劈吸声性能时必须予以考虑；敷设空腔尖劈的声呐平台区的振动及自噪声总声压级显著降低，尖劈部分优化敷设既要兼顾声呐基阵位置处的声压分布。

空腔尖劈；腔体能量耗散；吸声系数；声呐平台

1 引言

在水下结构表面敷设水声材料是应用最广泛也是非常有效的一种提高水下航行器隐身性能的方法［1］。尖劈吸声结构具有阻抗逐渐过渡的性质，在较低频率下具有优良的吸声性能，通过添加空腔、填料等可以增加其吸声频带宽度。在消声水池、大型消声室及水面舰艇上尖劈吸声结构得到广泛应用［2］。

尖劈吸声结构声场理论的研究有相当长的历史，然而由于其截面的不规则性及吸声性能影响因素的复杂性等原因，用严格的波动理论很难给出精确解，只能做近似计算，至今尚未建立严格的声场理论。尖劈吸声系数计算常用的方法是在截面上把尖劈材料和传声媒质的密度、压缩模量等声学参数按面积做某种计权平均得到等效参数［3］，然后按分层媒质声传播理论计算吸声系数［4］。王仁乾等类比变截面管中的声传播特性，应用变截面波动方程建立了尖劈吸声系数计算方程［5］。为了更加精准地反映尖劈结构对入射到其表面上的声波能量的吸收，本文对传统变截面波导理论吸声系数计算方法进行补充，以喇叭型空腔为例分析了声波在空腔中的传播规律，给出了计及空腔能量耗散作用的尖劈结构吸声系数计算方法。以腔尖劈材料力学参数及吸声性能测试数据作为输入，通过数值试验的研究了敷设空腔尖劈的声呐平台区的振动及声学特性，对比分析了空腔尖劈敷设方式对平台区声学特性的影响规律。

2 变截面波管理论

空腔尖劈结构中声传播特性与变截面管道中声传播问题类似，考虑尖劈材料为弹性介质，不考虑空腔内空气的影响，平面声波垂直于尖劈结构入射，声场满足变截面形式的波动方程［6］：

若波动方程的形式解 P ＝P（x）ejωt，则对于变量x的常微分方程可写为：

式中，k ＝ω／c；S′＝dS（x）／dx，式（2）～式（9）为变系数常微分方程，其解可表示为变系数的指数函数的组合：

式中，A（x）与 σ 为待定量；参数 B1，B2由边界条件确定，将式（3）代入式（2），得到如下关系式：

若使式（4）恒成立，其实部和虚部应分别等于0，得到如下2个方程：

由质点振速和声压关系，可得振速：

则在x点截面处的输入声阻抗：

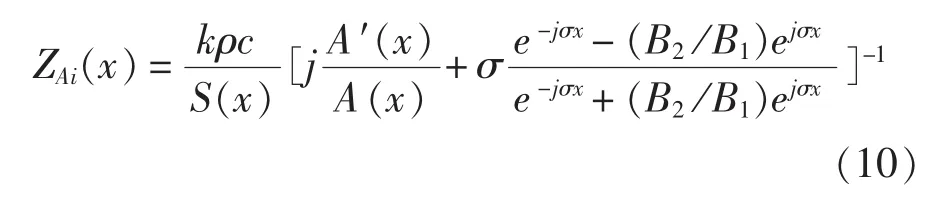
将声学覆盖层等分 n 个环形台面［7］，S0、S1、S2，…，Sn，分别为声学覆盖层的底面、环面和顶面的面积，声学覆盖层分层处理示意图如图1所示。

入射到声学覆盖层顶端和侧面的声波总能量可表示为［5］：

定义第 j个环形面的声强反射系数rj＝ Irj／Ii，则总的反射能量和吸收能量分别为：

空腔尖劈吸声结构顶端和各环形面声强反射系数由变截面波导理论得到：

式中，声学覆盖层顶端输入声阻抗 ZAm＝ρwcw／S0。

3 传统吸声理论的不足

运用传统的变截面波导理论来计算带有空腔的声学覆盖层结构，通过将声学覆盖层结构分层，把每层面积加权计算，然后得出等效实心聚氨酯吸声层。 对于截面 S（x）＝π［（x）－（x）］ ＝πr2（x）的带空腔的圆锥，r（x）是环形面的等效半径。

这种方法忽略尖了劈吸声结构腔体中空气对声波的耗散作用，将尖劈结构横截面按面积加权计算，得出每个截面的聚氨酯平均半径。其结果只是考虑了聚氨酯介质对声波能量的吸收和损耗，而忽略了腔体中的空气对声波能量的耗散。实际上，声学覆盖层腔体中的空气也耗散了部分声波能量。

因此，为了更加精准地反映出尖劈吸声结构对入射到其表面上的声波能量的吸收，有必要对传统的变截面波导理论吸声系数计算方法进行补充和修正，对计及腔体中空气作用的尖劈吸声结构吸声性能进行深入研究。

4 计及空腔作用的尖劈吸声结构吸声性能分析

以喇叭型聚氨酯空腔尖劈吸声结构为例，图2给出了喇叭型空腔示意图。假定原来封闭在距离x、x＋δx处的2个平面P、Q之间的气体在声波传递过程中移动P′Q′，P的位移是ζ，而Q的位移是 ζ＋ δζ。

以喇叭型空腔尖劈为例，空腔对称于它的中线，且截面积随距离按A＝A0e2ax变化，其中a和A0是常数。

利用腔型的变化规律，式（19）化为：

利用分离变量法，通解的形式是［9］：

其中，第1项表示向右移动的波，而第2项表示向左移动的波。喇叭空腔中波群速度为：

其中，ω＝kc。

由此可见声波沿着尖劈喇叭空腔速度依赖于频率和截面衰减因子，对式（21）求导可得到空气管中x点横截面上的质点速度u（x）：

根据以上理论对声波在尖劈空腔空气中的能量损耗进行计算。如图1所示，声波垂直于尖劈结构横截面入射，首先在聚氨酯介质中传播，通过式（9）可求出质点振速u（x）。当声波传播到空腔围壁时，由于聚氨酯和空气特性阻抗不同，横截面上不同部位的质点振速会发生变化。运用式（9）和式（23）分别求出尖劈聚氨酯中质点振速 u1（x）和空气中质点振速 u2（x），将 u1（x）和 u2（x）按横截面面积等效求出x点截面处质点振速u3（x），进而求出x点截面处的输入声阻抗，最后求得吸声系数。

S1为聚氨酯部分截面面积，S2空腔空气部分截面面积，u3（x）可表示为：

聚氨酯空腔尖劈试验具体尺寸为：L＝200 mm，l1＝80 mm，l2＝40 mm，l3＝40 mm，r1＝6 mm，r2＝12 mm

计及空腔能量耗散作用的尖劈结构吸声系数和传统变截面波导理论吸声系数对比曲线如图5所示。

从图5可以看出，考虑到空腔中空气对声波的能量吸收作用后，尖劈结构低频段吸声性能较传统方法有一定程度的增强，曲线谐振峰数值有所增大，高频段吸声性能略有下降。究其原因，尖劈吸声结构的吸声是由于声波透射到尖劈内部的声能被耗散，以及在声波作用下内部空腔所产生的共振吸收。中高频段以耗散吸声为主，低频段以共振吸收为主，当尖劈腔体发生共振时，腔内的空气柱会随整个腔体一起振动，进一步消耗了传入声波的能量。计及空腔中空气的吸声作用后，尖劈吸声结构低频段吸声性能加强，因而低频段吸声系数高于传统的变截面波导理论吸声系数。但是，这样会使尖劈结构截面等效平均半径减小，减弱了聚氨酯对传入声波的能量的损耗，因此高频段尖劈结构吸声系数曲线较传统的变截面波导理论吸声系数曲线略有下降。

由上述分析可以得出结论，腔体空气对中高频段声波的能量吸收有限，而对低频段声波能量吸收有很大作用。腔体中的空气是尖劈结构低频段吸收声能的一种非常重要的介质，在3 kHz以下频段计算空腔尖劈吸声性能时必须予以考虑。

本文通过声脉冲管法实验测试了空腔尖劈不同静压下的吸声系数，验证了本文算法的有效性。

如图6所示，随着水深的加大，吸声系数曲线形状基本不变，但尖劈吸声结构的吸声系数有所下降，静水压力越大，吸声系数下降越大，这主要是由于在静水压力作用下尖劈吸声结构产生形变，空腔的有效容积变小引起的。

分析图6、图7可以看出，本文采用计及空腔能量耗散作用的分层介质模型理论计算得到的尖劈吸声系数与实验结果在总体变化趋势上基本一致，这也证明了本文计算吸声系数理论方法的正确性。由于测试实验具有误差性，试验测试曲线在个别处出现凹凸，没有仿真计算曲线光顺。

5 空腔尖劈在声呐平台区中应用研究

由于声呐平台区为一复杂的混响场，其自噪声具有多声源特征，声呐平台区自噪声的预报除定量估算自噪声的量级大小外，还可以通过分析掌握不同噪声源对平台区自噪声的贡献量，为空腔尖劈的优化敷设方案提供依据，量化自噪声控制措施及其的技术指标［10］。

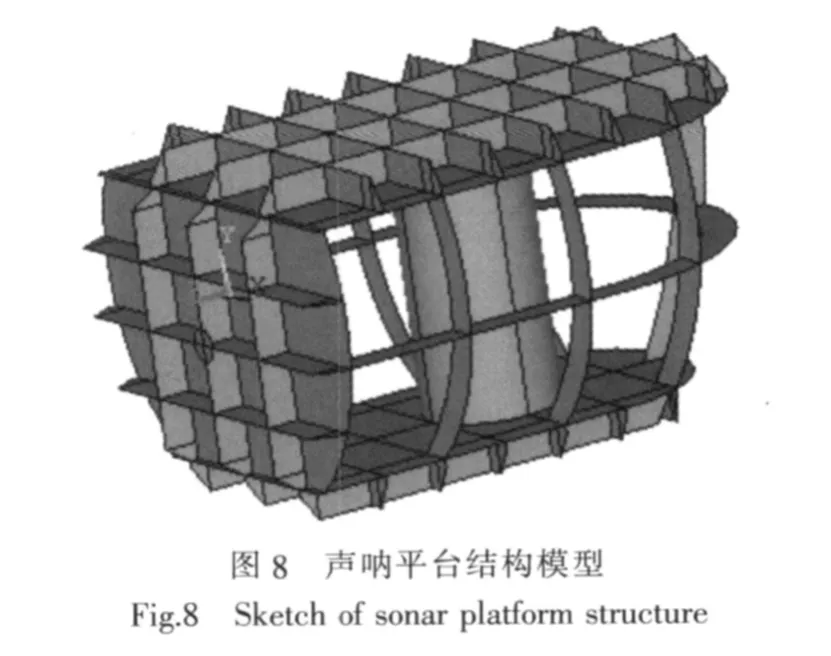
本文应用壳、梁和3D等单元构造一个接近于实艇的声呐平台一体化有限元模型，该模型不仅在形状上和实际结构相似，而且所有的几何参数和物理参数都是正确的。同时以腔尖劈材料力学参数及吸声性能测试数据作为数值试验的输入，低频采用声固耦合法，中高频采用SEA方法，数值计算了10 Hz～10 kHz的振动激励下，敷设空腔尖劈的声呐平台区的结构振动及自噪声响应，从而验证空腔尖劈的吸声作用。

为了对比分析空腔尖劈的减振降噪作用，以及不同敷设方式对平台区振动和声辐射特性的影响，从吸声尖劈的敷设方式方面设计了3种计算工况，具体工况描述如表1所示。

表1 空腔尖劈敷设工况Tab.1 Laying conditions of cavity wedge

图10所示为声呐平台敷设空腔尖劈前后结构的振动速度响应。可以看出，敷设吸声尖劈前后声呐平台的振动分布特性发生了一定改变，敷设吸声尖劈后声纳平台表面振动速度幅值在多数频点处有较大下降。

图11所示为平台区后壁的辐射声压级不同敷设工况下的对比曲线。可以看出，后壁对声呐平台区自噪声总声级的贡献量最大，后壁的辐射声压级的幅值和变化趋势基本决定了平台区的自噪声特性。

如图12、图13所示（限于篇幅只给出部分结果曲线），空腔尖劈60%敷设工况下上平台、声呐基阵安装位置的减振降噪效果甚至优于全敷设工况。因此，空腔尖劈的部分敷设方案及要考虑全频段声呐平台区的自噪声总声级，又要兼顾声呐基阵位置处的声压分布，从而最大程度地降低声呐平台区的自噪声，提高本艇声呐的探测距离和精度。

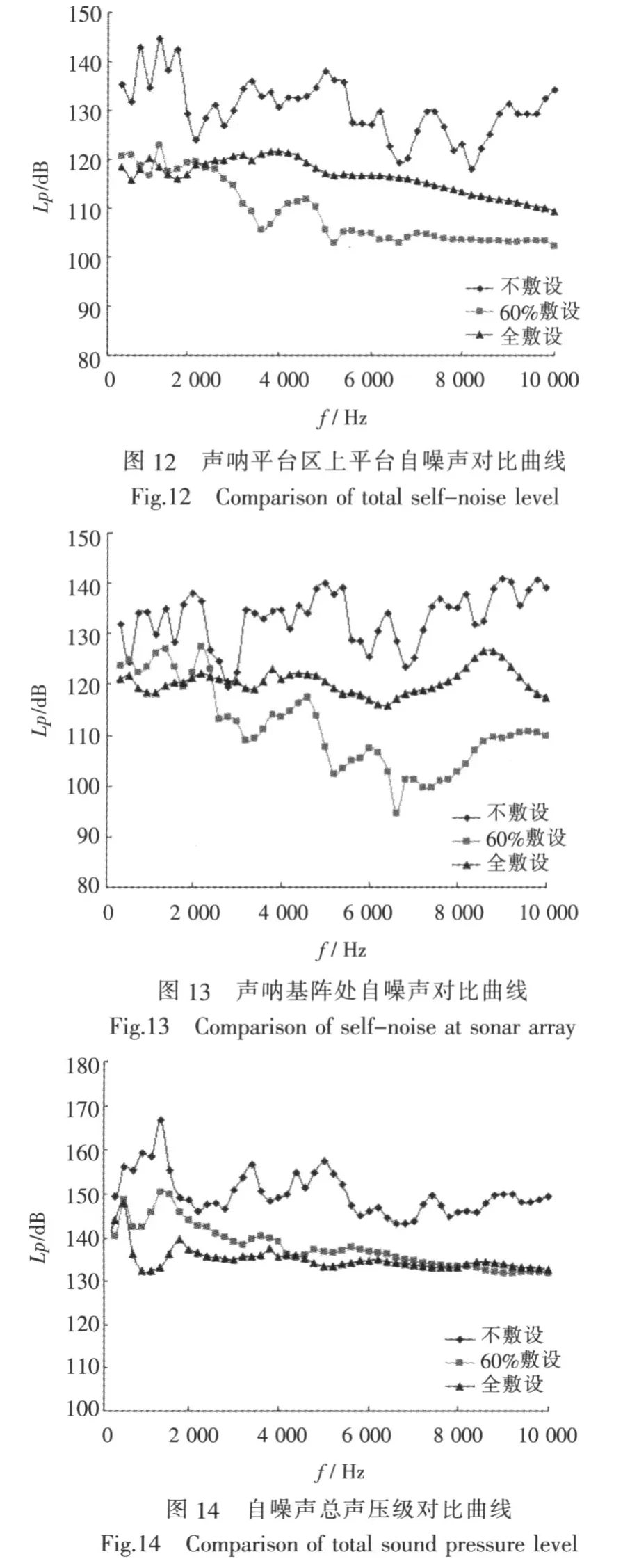
图14所示为声呐平台区自噪声总声压级不同敷设工况下的对比曲线。可以看出，空腔尖劈明显削弱了声呐平台区自噪声总声压级的峰值，曲线变化趋势和缓且全敷设与60%敷设工况曲线的变化趋势基本一致，其自噪声总声压级平均降低14 dB。60%敷设工况亦有较好降噪效果，声呐平台区自噪声总声压级平均降低11 dB，但是与全敷设工况相比中低频降噪效果要差一些。

6 结 论

本文以聚氨酯喇叭型空腔尖劈为例，分析了声波在空腔中的传播规律，给出了计及空腔能量耗散作用的尖劈结构吸声系数计算方法。通过数值试验研究了敷设空腔尖劈的声呐平台区的振动及声学特性，主要结论如下：

1）尖劈空腔对较低频段声波能量吸收有很大作用，在3 KHz以下频段计算空腔尖劈吸声性能时必须予以考虑；

2）扩大空腔尺寸可以增大空腔对声能的损耗作用，提高低频段尖劈的吸声效果，但过大的空腔尺寸会使尖劈结构等效阻抗与水失配严重，影响尖劈整体吸声效果；

3）空腔尖劈全敷设工况声呐平台区的减振降噪效果最好，平台区后壁对自噪声总声级的贡献量最大；空腔尖劈的部分敷设方案要兼顾声呐基阵位置处的声压分布。

［1］朱金华，王源升.水声吸声高分子材料的发展及应用［J］.高分子材料科学与工程，2005，21（4）：46－50.

［2］姜闻文，陈光冶，朱彦.静水压变化下橡胶结构吸声性能的计算与分析［J］.噪声与振动控制，2006，（5）：55－57.

［3］杨雪，王源升，余红伟.梯度聚氨酯吸声性能研究［J］.武汉理工大学学报，2008，30（3）：21－23

［4］HABERMAN M R， YVES H B， JARZYNSKI J， et al.Micromechanical modeling of viscoelastic voided composites in the low frequency approximation ［J］.J.Acoust.Soc.Am，2002，112（5）：1937－1943.

［5］王仁乾，马黎黎.基材含微粒的空腔结构吸声器吸声性能预报的研究［J］.声学技术，2006，25（3）：175－181.

［6］ONURSAL O， MEHMET C.Design of a single layer micro－perforated sound absorber by finite element analysis［J］.Applied Acoustics，2010，71（4）：79-85.

［7］何曼君，陈维孝，董西侠.高分子物理［M］.复旦大学出版社，

［8］DAVID M.Acoustic waves in elastic solids［M］.Spon Press，Oxon，2007.

［9］ZOU J，SHEN Y，YANG J，et al.A note on the prediction method of reverberation absorption coefficient of double layer micro－perforated membrane ［J］.Applied Acoustics，2006，67（2）：106-111.

［10］姚熊亮，计方，庞福振，等.聚氨酯空腔尖劈吸声性能实验研究［J］.振动与冲击，2010，29（1）：88－93.

Acoustic Characteristics of Wedge Structure Taking Account of Cavity Energy Dissipation

Ji Fang Yao Xiong－liang
College of Shipbuilding Engineering， Harbin Engineering University， Harbin 150001， China

Taking horn cavity as an example， the rule of sound propagation in cavity was researched，and the amended calculation method taking account of energy dissipation in the cavity was summed up.The validity of calculation method was also verified through sound pulse pipe test.Furthermore， the vibration and self－noise distribution of sonar platform was predicted through numerical experiment.The influence of cavity wedge laying conditions to sonar platform acoustic characteristics was analyzed.The results show that the cavity acoustic energy absorption is very effective in low frequency，and the calculation of cavity wedge acoustic performance must be taken into account below 3kHz.The laying of cavity wedge obviously reduces the vibration level and total self－noise level of sonar platform， part laying method of wedge must consider the pressure distribution of sonar array.

cavity wedges； cavity energy dissipation； sound absorption coefficient； sonar platform

U661.44

A

1673－3185（2011）03－73－06

10.3969/j.issn.1673-3185.2011.03.016

2010-07-21

国防重点预研项目（4011*****0201）；国防科技合作项目（2007DFR80340）

计 方（1984－），男，博士研究生。研究方向：船舶振动噪声控制。E-mail：heujifang＠163.com