船舶尾轴承倾斜计算分析研究

张少凯 周建辉 吴 炜 魏颖春

1海军驻大连船舶重工集团有限公司军事代表室，辽宁 大连 116011

2中国舰船研究设计中心，湖北 武汉 430064

3武汉理工大学 能源与动力工程学院，湖北 武汉 430063

船舶尾轴承倾斜计算分析研究

张少凯1周建辉2吴 炜2魏颖春3

1海军驻大连船舶重工集团有限公司军事代表室，辽宁 大连 116011

2中国舰船研究设计中心，湖北 武汉 430064

3武汉理工大学 能源与动力工程学院，湖北 武汉 430063

为改善船舶尾轴承受力状况，应用有限元方法建立船舶尾轴承与尾轴接触模型，对其进行计算分析，研究降低轴承峰值压力的措施。计算结果表明，改善压力分布可采用倾斜尾轴承方式，轴承倾角大小应以尾轴弹性变形曲线为依据。倾角太小起不到增加尾轴承接触面积和降低峰值压力的目的；倾角过大可能导致尾轴承前端与尾轴接触，轴承尾端出现腾空现象。

船舶尾轴承；接触压力；倾斜角度；计算分析

1 引言

尾轴承是船舶动力装置中工作条件最恶劣的部件之一，国内外对此开展许多相关研究［1－5］。 为保证尾轴承具有良好的工作性能，船舶规范对其长径比L／D作了严格规定，如白合金尾轴承为2～2.5，赛龙、橡胶等高分子材料尾轴承为4。但由于螺旋桨的悬臂作用，尾轴产生过大弯曲变形，尾轴承的实际接触长度较设计长度要短，接触面积要小，导致尾轴承边缘效应，局部压力过高，润滑不良，出现过大的振动与噪声，使用寿命缩短。

本文基于ANSYS有限元方法，以弹性接触计算为研究手段，对船舶后尾轴承展开研究，建立轴系有限元模型，并在尾轴承支承处建立接触单元，进行尾轴承受力分析，提出增加接触面积，降低轴承峰值压力的措施，以改善尾轴承的使用性能，延长工作寿命。

2 尾轴承有限元计算模型

某船轴系与主机曲轴的末端共有7个支承轴承［6］。其中包括2个尾轴承、1个中间轴承、2个推力轴承和2个主轴承。轴系没有推力轴，推力轴承安装在主机内，由尾端（螺旋桨）至首端（曲轴倒数第2个主轴承）全长共16.64 m，轴系各轴承跨距 l1～l7依次为 1 220 mm、2 400 mm、4 400 mm、3 900 mm、1 020 mm、1 140 mm、1 140 mm， 如图 1所示。轴系的主要参数如下：中间轴轴径460 mm；尾轴轴径600 mm；尾轴承材料为白合金；尾轴承长度1 500 mm；尾轴承内径600 mm；尾轴承长径比 2.5∶1；螺旋桨空气中质量 14.64 × 103kg。

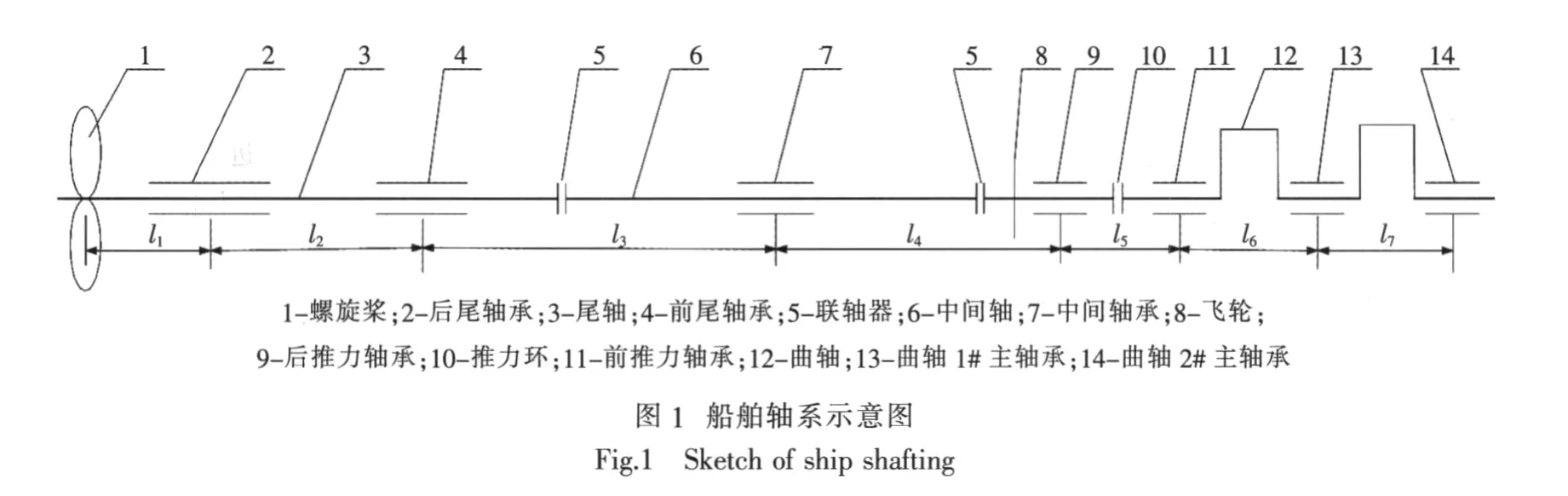
采用ANSYS单元库中Beam188单元模拟船舶轴系受力状态。轴系以导流罩处为尾端，以主机倒数第二个主轴承处为首端。建模时，导流螺帽、螺旋桨、飞轮、推力环和活塞连杆机构按照集中载荷处理，除尾轴承外，轴承支承处施加垂向约束，尾轴承衬套外边面施加x、y和z 3个方向的约束，首尾按照自由端处理，如图2（a）所示。

尾轴和与尾轴承相配合的轴段采用8节点实体单元Solid185进行模拟，在尾轴外表面与尾轴承内表面接触处覆盖一层接触单元，并建立接触对模拟尾轴承真实受力状况。轴系其他部分采用2 节 点 Timoshenko 梁 Beam188 单 元 进 行 模 拟［7］，如图 2（b）所示。

由计算结果（见表1）可以得到尾轴承的负荷W为217 kN，理论平均比压（轴承设计单位面积比压）为 W／（D×L）＝0.24 MPa。

表1 各轴承负荷Tab.1 Load of bearings

3 尾轴承倾斜分析

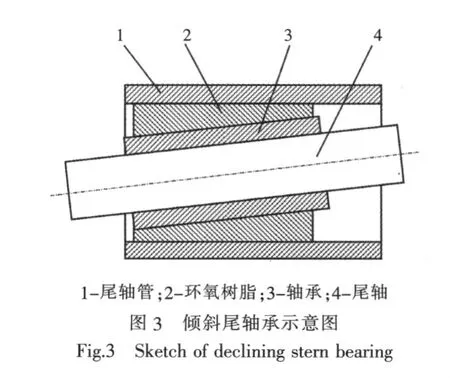
尾轴承与尾轴的接触面积决定压力的大小与分布，对轴承承载能力有重要的影响。由于螺旋桨的悬臂作用，导致尾轴承边缘效应，接触面积减小，峰值压力增大。目前，采用斜镗尾轴孔或倾斜尾轴承是增加尾轴承接触面积，降低峰值压力的重要方法之一，尤其倾斜尾轴承方法施工方便，较为常用，如图3所示。

是否采用倾斜尾轴承方法，各国船级社的标准并不统一。英国劳氏船级社规定尾轴转角超过3.0×10－4rad为标准，美国ABS认为这一规定的理由不充分，但进行实际计算时，他们还是以3.0×10－4rad为标准；中国船级社CCS认为转角超过3.5×10－4rad， 可采用倾斜尾轴承； 挪威船级社DNV则重新定义尾轴承与尾轴相对名义转角［8］，并制定相应的转角安全标准，如图4所示。

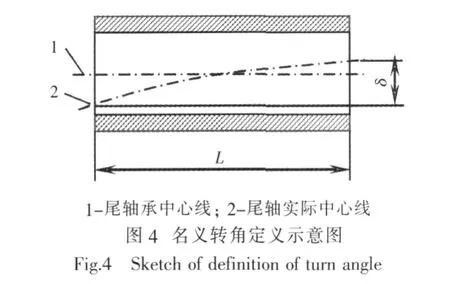
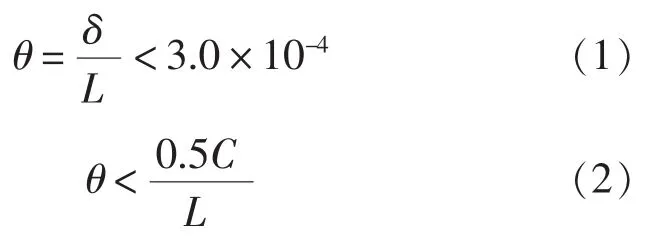
式中，θ为尾轴承与尾轴相对名义转角，rad；L为尾轴承长度，mm；δ为尾轴中线首尾端高度差，mm；C为尾轴承与尾轴安装间隙，mm。

DNV认为尾轴承与尾轴相对转角同时满足式（1）和式（2）时，尾轴承不需要倾斜，否则需要考虑。

由此可见，各国船级社对尾轴承转角的标准都制定了参考标准，其依据是尾轴的弹性变形曲线。本船尾轴的弹性曲线如图5所示，该弹性变形曲线反映了在外力作用下尾轴的垂向弯曲程度，而转角（尾轴中心线和尾轴承中心线的倾斜程度）反映了尾轴与尾轴承接触状况。

由于尾轴的轴线呈二次抛物线形状，因此在各个位置的转角不同。安装在白合金尾轴承上的尾轴变形、转角情况如表2所示。

从表2可以看出，该尾轴段最大转角为1.91×10－4rad，且从尾端到首段转角不断减小。 为了增加尾轴与尾轴承的接触面积，尾轴承需要选择合适的倾斜角度与尾轴的弹性曲线相匹配。

4 尾轴承倾斜计算

继续采用尾轴承有限元计算模型对倾斜后的尾轴承与尾轴进行接触仿真计算。尾轴承倾斜之后，尾轴承上的支承位置会发生变化，尾轴的弹性变形曲线也可能会发生改变，这里分别选取0.5×10－4、1.0 × 10－4、1.5 × 10－4和 2.0 × 10－44 个倾斜角度进行白合金尾轴承接触面积与峰值压力对比。

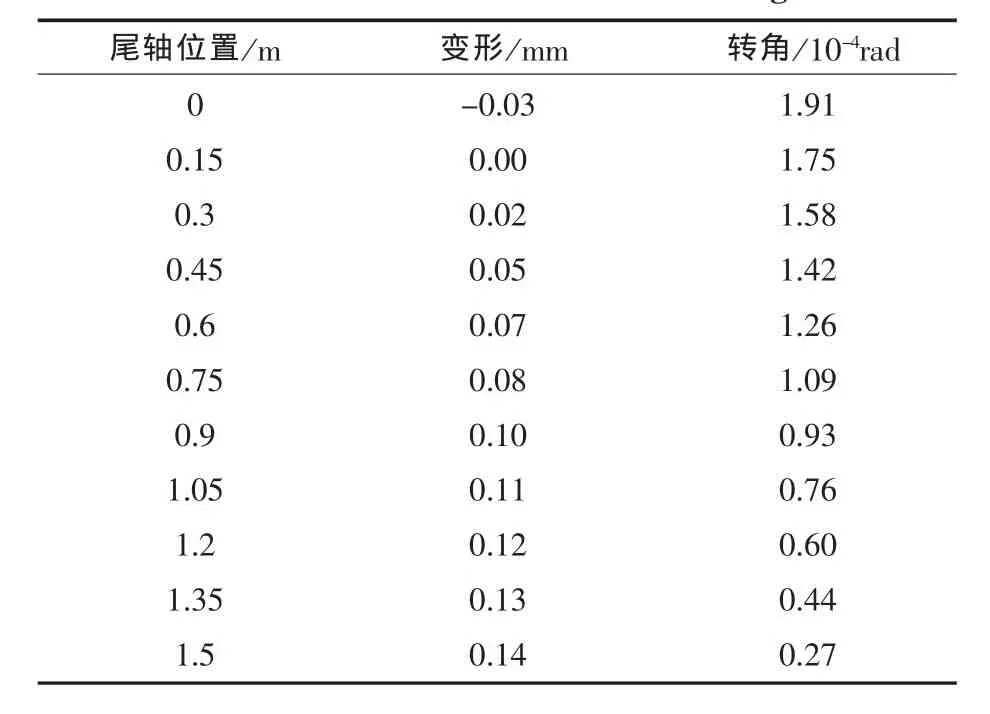
表2 尾轴转角数据表Tab.2 Data table of tail shaft turn angle

1）接触面积比较

通过有限元计算，尾轴承的4个倾斜角度的接触面积如图6所示。

从图6可以看出，白合金尾轴承接触对区域倾斜角度并不是太敏感，接触长度并没有发生较大的变化。由于白合金轴承弹性模量比较高，刚度较大，变形较小，与尾轴接触状况不大理想，容易造成尾轴部分腾空，局部负荷过大，甚至出现轴承两端接触的情况，如图 6（b）～图 6（d） 所示。 随着尾轴承倾斜角度的增加，轴承的支点会向首端转移。 0.5 × 10－4rad 时，只有尾端接触；1.0 ×10－4rad时，首段也出现部分接触区域，但支承中心还是在尾端；1.5 ×10－4和 2.0×10－4rad 时，首尾两端都发生了接触，支承中心转移到首端。

发生上述情况是因为倾斜计算时采用直线进行逼近方法。尾轴轴线的变形为二次曲线，当倾斜角度较小时，主要是尾端接触，当倾斜角度较大时，且尾轴首端转角较小时，则导致首端与尾轴先发生接触。

2）峰值压力比较

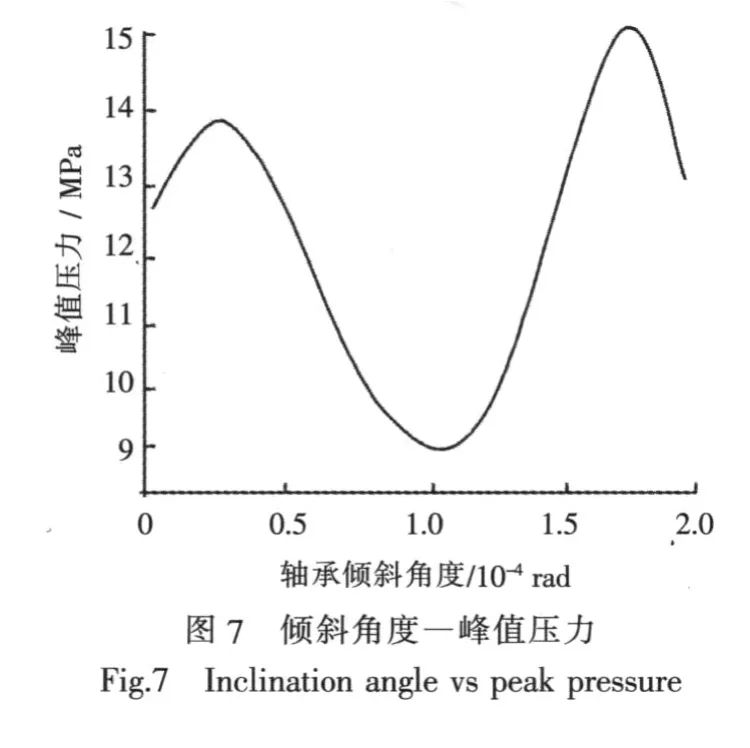
倾斜角度与峰值压力分布状况见图7所示。由图可见，峰值压力为二次曲线。当倾斜角度在1.0×10－4rad时，峰值压力最小。 这时轴承尾端与尾轴接触良好，首端也出现部分接触，首尾两点直线倾斜角度约为 1.0×10－4rad； 当倾斜角度为2.0×10－4rad 时，首端接触，峰值压力下降，但这不是理想的结果。过大的倾斜角度可能会造成压力中心转移到首端，尾端腾空，实际上抬高了尾轴承的垂向位置，这对于其他轴承的承载不利，容易出现负荷，这是不允许的。

5 结 论

1）基于ANSYS有限元方法对船舶轴系受力计算和尾轴承倾斜接触分析计算，可较好地模拟尾轴承在不同倾斜角度下与尾轴的接触情况，为船舶尾轴承的设计提供理论参考。

2）尾轴承倾角过小不利于增加接触面积，过大则可能导致尾轴承首端与尾轴接触，甚至引起其他轴承腾空，出现负负荷。因此，选择合适的尾轴承倾角，有助于增加轴承接触面积，降低峰值压力。

［1］俞强，郭全丽.潜器轴系校中计算研究［J］.船海工程，2003，157（6）：32－34.

［2］杨和庭，唐育民.船舶水润滑尾管橡胶轴承的设计［J］.武汉造船，2000（2）：19－22.

［3］ALES D K，RON A J.Calculation of Stribeck curves for water lubricated journal bearings ［J］.Tribology International，2007，40（3）：459－469.

［4］刘正林，周建辉，朱汉华，等.计入尾轴倾角的船舶尾轴承液膜压力分布计算研究［J］.武汉理工大学学报，2009（9）：111－113.

［5］周春良，刘顺隆，郑洪涛.船舶艉管轴承内部流场数值分析［J］.船舶工程，2006（28）：26－29.

［6］温玉奎.57300 DWT散货船轴系校中研究 ［D］.大连海事大学，2007.

［7］尚晓江.ANSYS结构有限元高级分析方法及范例应用［M］.北京：中国水利水电出版社，2005.

［8］许运秀.主推进轴系校中状况分析与对策（中）［J］.中国船检，2008（11）：87－88.

Computational Analysis on the Inclination of Ship Stern Bearing

Zhang Shao－kai1 Zhou Jian－hui2 Wu Wei2 Wei Ying－chun3
1 Military Representative Office in Dalian Shipbuilding Industry Co.， Ltd， Dalian 116011， China
2 China Ship Development and Design Center， Wuhan 430064， China
3 School of Energy and Power Engineering， Wuhan University of Technology，Wuhan 430063， China

In order to improve the strained condition of marine stern bearing， the contacting model of both marine stern bearing and tail shaft was built with Finite Element Method，then computed and analyzed to research the measurement for reducing peak pressure of the stern bearing.The computation results indicate that the stern bearing inclination is often used to improve the pressure distribution.The angle of inclination of a stern bearing is depended on the elastic deformation curve of the tail shaft.The smaller angle of inclination cannot increase the contacting area and reduce peak pressure，but overlarge angle may make the lead end of stern bearing contacted to the tail shaft and the backend emptied out.

marine stern bearing； contacting pressure；inclination； calculation

U664.21

A

1673－3185（2011）03－60－04

10.3969/j.issn.1673-3185.2011.03.013

2010-04-09

湖北省自然科学基金项目（2008CDA027）

张少凯（1966－），男，学士，高级工程师。研究方向：轮机工程。E-mail：dongtingdao＠tom.com

周建辉（1974－），男，博士，工程师。研究方向：船舶动力装置。