耦合板结构振动波传递及能量分布可视化研究
2011-02-27李凯,黎胜,赵德有
1 引 言
动力设备在海洋工程及船舶结构中引起的振动能量传递一直以来都是工程师和研究人员所关心的重要研究方向之一。在实际振动结构中,能量以弯曲波、剪切波和纵波三种形式传播,其中弯曲波携带大部分的能量;而纵向、剪切运动与振动能量在耦合结构中传播密切相关[1]。
振动波在经过结构转角和连接处会发生波形的转换和能量传递。Cuschieri和McCollum[2]基于功率流法研究了耦合平板连接处的面内波和弯曲波功率流特性。Wang和Xing[3]基于子结构法研究了L形板振动功率流。Kessissoglou[4]研究了面内纵波和剪切波对L形连接板振动功率流的影响,运用功率流的方法,比较了各种波形对转角连接处功率流传递的贡献。李天匀等[5]利用导纳方法研究了L形加筋板在外载荷作用下的输入振动功率流和传递振动功率流。周平和赵德有[6]基于动态刚度阵法计算了加筋板在中高频区域内的振动能量比,并通过与统计能量分析方法和有限元方法的计算结果比较,验证了方法的可行性和高效性。伍先俊[7]从有限元动力方程推导出发,给出了节点频域复数力的表达式,进而给出基于有限元动力分析的功率流计算方法,但计算处理过程比较复杂,不便于工程应用。谢基榕[8]在Msc/Nastran的基础上二次开发了结构功率流分析模块,并对悬臂梁结构进行了功率流分析。但是该功率流分析模块并未集成流线可视化技术,在图像可视化方面还需进一步完善。
许多学者针对板中的能量流特性进行了研究。Bernhard[9]首次提出用时域和空间平均的能量密度矢量来研究结构声在板中的传递。Bouthier[10]和Ichchou[11]等学者进一步将热传导理论应用于板能量流动数学模型中,同时证明了该理论可以推广到二维平面波传递中。
振动声强法(vibration intensity method)是上世纪七十年代由Noiseux[12]将空气声学中的声强理论移植到连续介质力学上,考虑了结构内力和质点响应,研究弹性介质中单位宽度截面上的功率流,它可以认为是功率流密度[13]。振动声强技术突出的优势在于可以提供结构中任意位置振动能量流的强度和方向等重要信息,并且不依赖于边界条件[14-15]。 等[16]基于复模态理论,将外力和弯矩荷载引入振动声强的理论表达式,利用有限元法计算了简支板的能量流分布情况。Khun等[17]探讨了不同外部阻尼敷设位置及阻尼系数对振动能量传递路径的影响,并对离散螺栓连接板的振动声强传递特性进行了研究。此外,很多学者将振动声强法用于复合材料和波纹板结构中的结构声传递研究中。
本文便是通过自编MATLAB程序调用有限元动力分析软件ANSYS,自行完成振动声强分量及能量流计算等工作,然后根据输出数据进行图像流线和云图显示,揭示振动结构中能量流传递和分布。振动波传递集成可视化程序可以方便应用于复杂结构物减振降噪工程中。
2 结构振动声强基本理论
Pavic[14]给出了结构瞬态振动声强的时域平均表达式为:

式中,σij(t)和 vj(t)为应力分量和速度分量。
根据弹性薄板理论,(1)式中Ix可以表示为:

其中,G=E/(1-2 μ),E为弹性模量,μ 为泊松比,φx和 φy为转角,ξΜ为质点在x方向的位移,h为板厚,vx,vy,vz为速度分量。板单元的广义力和位移如图1所示。
结构振动波通过内力(Qx和 Qy),面内力(Nx,Ny和 Nxy)弯矩(Mx和 My)和扭矩(Mxy和 Myx)来传递能量,则对于x方向的振动声强分量可以表示为:

其中内力和弯矩分量可由下述公式计算:
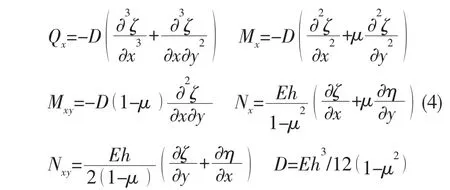
对于二维板单元,给出振动声强的频域表达式[9]为:
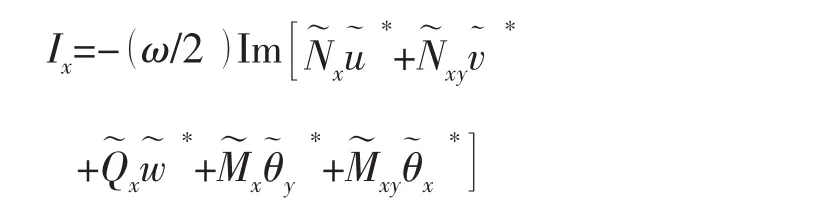


图1 板单元的广义力和位移Fig.1 Plate element with defined force and displacement
流线图[18]可以直观表征振动能量传递路径,通过这种流线可视化技术,可以准确分析和理解复杂结构中能量的流动形式以及能量涡流特性。应用向量代数运算公式,流线上应满足

式中,r为能量流动的方向坐标。
则对于三维连续介质,流线方程变为

对于二维板结构,可以表示如下:

3 板结构振动能量流
在平板结构中,弯曲波携带主要的振动能量,并在声辐射中起主要作用,因此本文对(2)式进行简化,仅考虑弯曲波分量,对其在板厚方向进行积分,可以得到单位长度板横截面中瞬态能量流的公式为:

而对于耦合结构,纵向、剪切运动与振动能量传播密切相关,并可以引起连接构件的弯曲振动,不能忽视[4]。因此在研究L形耦合板振动能量分布时,需引入剪切波和纵向波分量。
通过计算单位时间内通过振动结构特征面积的能量来获取各种波形总的振动能量[19]。考虑板的纵向振动模态,可得纵向波振动能量流为EL:

同理可得板的弯曲波振动能量流为EB:

板的剪切波振动能量流为ES:

其中,CL=为弹性波在板中传播的波相速度,ρ为单位表面积质量密度。则弹性结构中总的能量流E等于上述三种波形能量之和,即:

4 可视化程序实现
本文基于MATLAB软件和APDL程序语言对ANSYS进行二次开发,充分发挥ANSYS对复杂结构建模和强大的结构动力分析能力。采用MATLAB作为主控程序,设置好所有的参数与选项传递给ANSYS(通过文件)并调用计算。计算结束后再用MATLAB处理ANSYS的输出文件,完成自编程序和ANSYS软件的相互调用,实现振动能量流的集成可视化显示。流程图如图2所示。
5 数值计算
5.1 方法验证

图2 程序流程图Fig.2 The flow chart of program

表1 矩形板的具体参数Tab.1 Parameters of plat plate
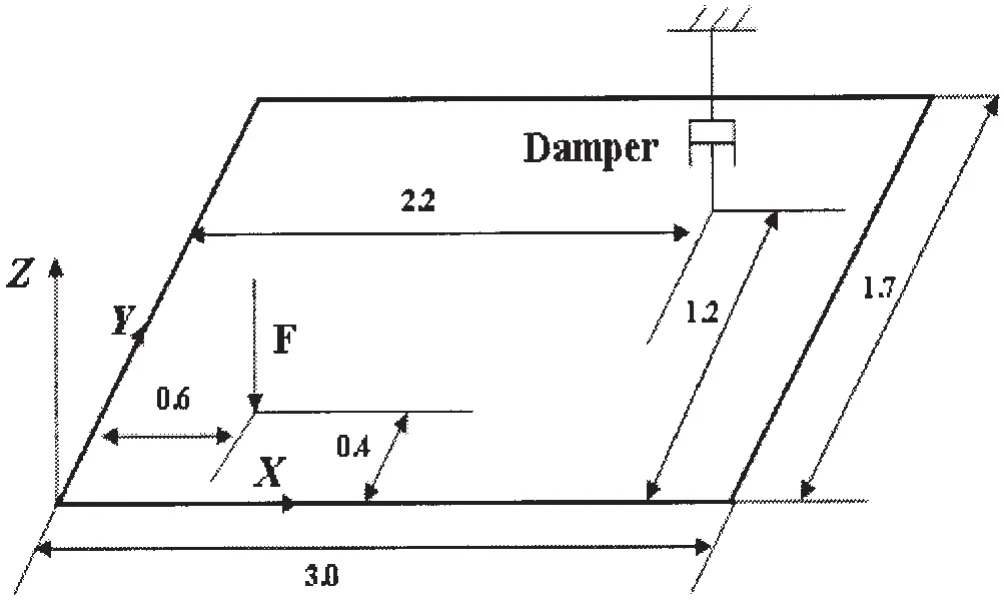
图3 文献[14]中板结构示意图Fig.3 Plat plate showing positions of force and damper in Ref.[14],the plate was simply supported along the edges
首先为了验证本文计算方法的准确性,采用文献[14]四边简支钢板为例进行计算,板的具体参数如表1所示,结构尺寸,激励力位置和阻尼器安置位置如图3所示,边界条件取四边简支,忽略结构阻尼影响,有限元模型由510个8节点等参shell93单元进行模拟,谐响应分析采用完全法进行计算。振动声强矢量结果(声强矢量未标准化处理)如图4(a)所示,能量从激励点流出,汇集到阻尼器位置被吸收,通过与文献[14]所列结果进行比较可得,本文声强分量计算方法及可视化程序实现是准确可行的。同时基于公式(9)计算了平板结构中的弯曲波振动能量流如图4(b)所示。

图4 本文方法计算振动声强矢量图和能量云图Fig.4 Vector representation of structural intensity and energy distribution for a flat plate
5.2 耦合板振动波传递及分布特性
本节以海洋工程结构中常见的耦合板为研究对象,结构尺寸、简谐集中力位置(0.6,0.5,0)和阻尼器位置(0,0.7,1.3)如图5所示,边界条件取短边对边简支,耦合边界处取自由,则面内波可以在边界处传输能量。有限元网格模型见图6。材质为钢板,具体参数见表2,简谐力、外部阻尼系数同上。根据L形耦合板结构固有频率和谐响应计算结果,选取了有代表性的前四阶固有频率f=8.5Hz,f=32Hz,f=69Hz,f=94Hz进行振动声强参数的计算,利用可视化技术给出相应的流线图和能量云图。

图5 L形耦合板示意图 单位(m)Fig.5 L-shaped plate showing positions of force and damper(m)

图6 有限元模型Fig.6 Finite element mesh of L-shaped plate

表2 L形耦合板的具体参数Tab.2 Parameters of L-shape plate
由图7(a)和图7(b)可以明显地看出,在激励频率为f=8.5Hz时,大部分振动能量从激励点流出,在阻尼器位置被吸收,能量的源点即为简谐集中力输入点,主要汇集于外部阻尼器所在位置,能量的流动路径比较清晰。可以看到,振动波在传输过程中,在耦合边界处出现了一定的反射。
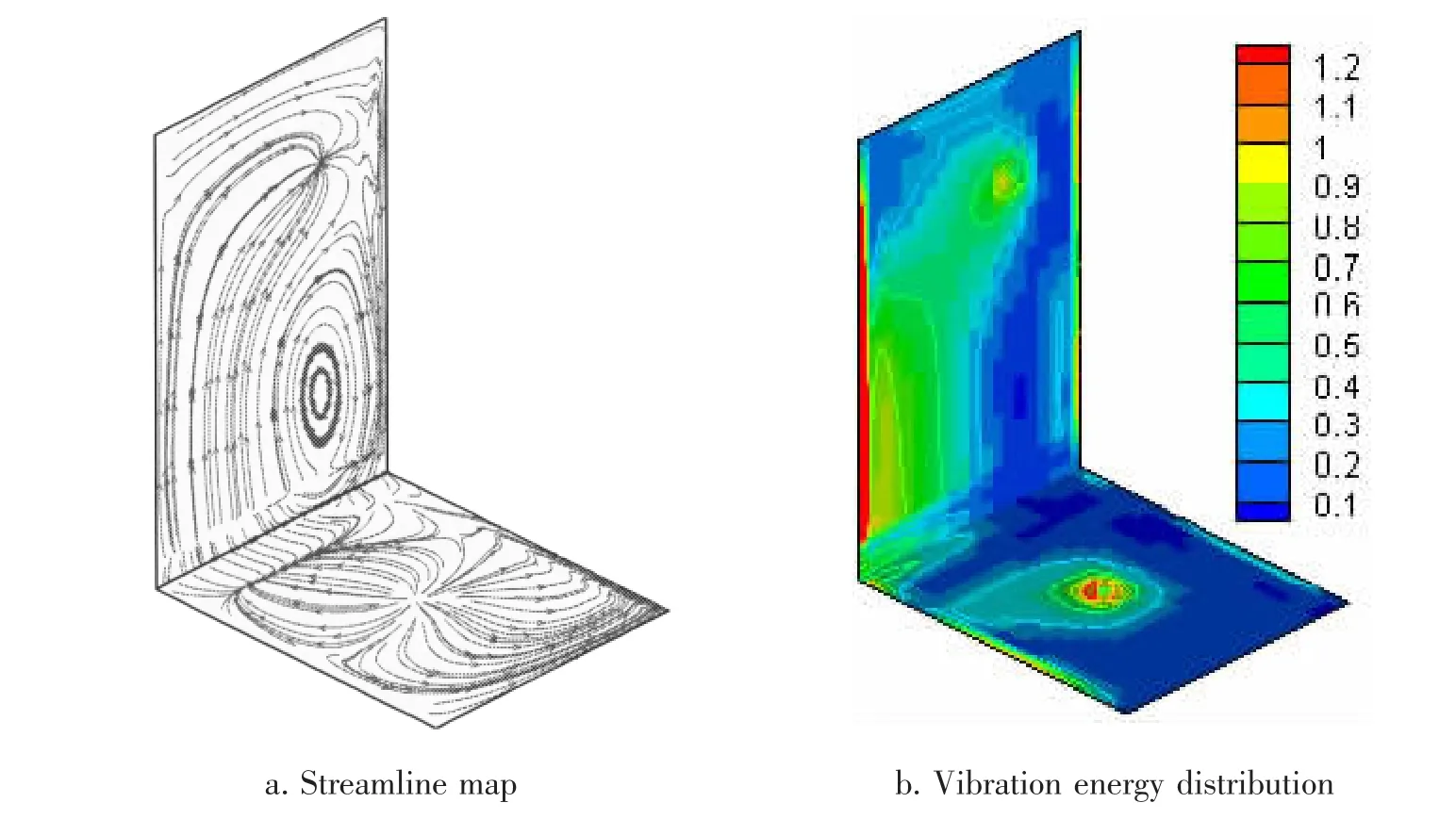
图7 振动声强流线图(a)和能量云图(b),f=8.5HzFig.7 Streamline(a)of structural intensity and vibration energy distribution(b)representation for the L-shape plate,f=8.5Hz

图8 振动声强流线图(a)和能量云图(b),f=32HzFig.8 Streamline(a)of structural intensity and vibration energy distribution(b)representation for the L-shape plate,f=32Hz
对比图7和图8看出,振动能量的分布可以非常直观地显现出来,能量的强弱分布与振动声强矢量图比较吻合。但随着激励频率的不同,能量分布也出现了明显的变化,从图7(b)可以看出,能量在激励点位置、板2的自由边分布最多,同时只有少部分能量通过耦合边界到达阻尼器位置。
随着激励频率的升高,从图9可以看出,振动能量传递路径更加复杂,能量从激励点流出,并没有完全传递到阻尼器位置,而是密集分布在板2,且出现了较明显的涡流场。大部分的能量汇集在板2涡流场位置和自由边界处,有一部分的能量传递到阻尼器位置点。
当激励频率的升高到94Hz时,从图10可以看出,振动能量传递路径更趋复杂,涡流分布也比较密集。大部分的能量分布在板1简谐激励力附近、板2自由边界处和耦合边界处。

图9 振动声强流线图(a)和能量云图(b),f=69HzFig.9 Streamline(a)of structural intensity and vibration energy distribution(b)representation for the L-shape plate,f=69Hz

图10 振动声强流线图(a)和能量云图(b),f=94HzFig.10 Streamline(a)of structural intensity and vibration energy distribution(b)representation for the L-shape plate,f=94Hz
6 结 论
本文利用自编程序实现了振动声强及能量可视化技术,并研究板结构中振动能量流向及分布,得到以下结论。
(1)本文基于MATLAB软件和APDL程序的集成可视化技术可以为结构声源识别提供直观的图像显示,并可以实现振动结构中能量流传递和分布的可视化,流线可视化技术可以直观显示能量的流动路径和涡流特性,文中算例提供了有力的验证。振动能量流的集成可视化显示程序可以方便地应用于复杂结构物减振降噪工程中。
(2)借助于能量云图可以更准确揭示振动能量在结构中的分布,并在分析振动波在复杂结构中的传播机理及进一步实施主/被动控制中提供更准确的科学依据。
[1]Cremer L,Heckl M,Ungar E E.Structure-borne Sound[M].Second Edition.Berlin:Springer-Verlag,2005.
[2]Cuschieri J M,McCollum M D.In-plane and out-of-plane waves power transmission through an L-type junction using mobility power flow approach[J].Journal of the Acoustical Society of America,1996,100(2):857-870.
[3]Wang Z H,Xing J T,Price W G.An investigation of power flow characteristics of L-shaped plates adopting a substructure approach[J].Journal of Sound and Vibration,2002,250(4):627-648.
[4]Kessissoglou N.Power transmission in L-shaped plates including flexural and in-plane vibration[J].J Acoust.Soc.Am.,2004,115:1157-1169.
[5]李天匀,张维衡.L形加筋板结构的导纳功率流研究[J].振动工程学报,1997,10(1):112-117.
[6]周 平,赵德有.基于动态刚度阵法的加筋板间能量流研究[J].大连理工大学学报,2008,48(1):98-104.
[7]伍先俊,朱石坚.基于有限元的功率流计算及隔振系统优化设计技术研究[J].船舶力学,2005,9(4):138-145.
[8]谢基榕,吴文伟.基于有限元的功率流分析方法及实现[J].船舶力学,2009,13(1):144-149.
[9]Bernhard R J,Bouthier O.Model of the space averaged energetics of plates[J].AIAA Paper 90-3921,1990.
[10]Bouthier O,Bernhard R J.Simple models of energy flow in vibrating plates[J].Journal of Sound and Vibration,1995,182:149-164.
[11]Ichchou M N,Jezequel L.Comments on simple models of the energy flow in vibrating membranes and transversely vibrating plates[J].Journal of Sound and Vibration,1996,195:679-685.
[12]Noiseux D U.Measurement of power flow in uniform beams and plates[J].Journal of the Acoustical Society of America,1970,47(1):238-247.
[13]Pavic G.Measurement of structure borne wave intensity[J].Journal of Sound and Vibration,1976,49(2):221-230.
[14]Gavric L,Pavic G.A finite element method for computation of structural intensity by the normal mode approach[J].Journal of Sound and Vibration,1993,164(1):29-43.
[15]Hambric S A,Taylor P D.Comparison of experimental and finite element structure-borne flexural wave power measurements for straight beam[J].Journal of Sound and Vibration,1994,170(5):595-605.
[16] J,Bochniak W.Vibration energy flow in ribbed plates[J].Mechanics,2006,25(3):119-123.
[17]Khun M S,Lee H P,Lim S P.Structural intensity in plates with multiple discrete and distributed spring-dashpot systems[J].Journal of Sound and Vibration,2004,276(3):627-648.
[18]Xu X D,Lee H P,Lu C,Guo J Y.Streamline representation for vibration intensity fields[J].Journal of Sound and Vibration,2005,280:449-454.
[19]尼基福罗夫·阿·斯.船体结构声学设计[M].北京:国防工业出版社,1998.
