舰艇螺旋桨水下噪声预测

杨琼方，王永生，张明敏

（1海军工程大学a.船舶与动力学院；b.水声研究所，武汉 430033）

1 引 言

无论是水面舰艇还是潜艇，声隐身性能都是衡量其战斗力的重要指标。水面舰船通常在航速大于10kns下运行时，都有充分发展了的螺旋桨空泡，这种声源左右了由5Hz到100kHz的全部辐射噪声[1-2]。至于潜艇，其活动能力也受到螺旋桨噪声的限制，二战时期声纳监听人员能听到的主要是螺旋桨噪声，在当时声纳工作的声频段（约6kHz），螺旋桨空化后的声级可能比空化前高出30～40dB。另外，在空泡筒中试验时，发现空泡出现之前，先出现高频声讯号，随后才看到空泡，整个噪声谱级都会增加。由此，目前已公认螺旋桨噪声是最主要的舰船噪声源，并且普遍承认螺旋桨空化是最强的辐射噪声源。螺旋桨噪声预测作为一个与水面舰船和潜艇战斗力休戚相关的命题，一直是工程设计人员所关注的对象。

在低频段，螺旋桨噪声表现为频率为叶频整数倍的线谱声，文献[3-4]对此进行了分析。本文主要分析特征频率以上高频段的螺旋桨噪声谱。依据已公布的水面舰船和潜艇螺旋桨噪声谱曲线图以及螺旋桨空泡筒实测经验，首先分析了螺旋桨噪声平坡形谱曲线的特点，给出了无空化状态和空化状态下噪声源声级谱曲线衰减指数值，分析了“声学空泡”产生后噪声谱曲线特征频率以及峰值谱级的影响因素。然后，利用文献[2]给出的声强表达式和文献[5]给出的螺旋桨空化状态下两个特征航速对应的部分频段内谱级的计算式，推广得到了水面舰船在螺旋桨发生空化后的任意可行航速下的噪声谱曲线图以及整个频段内的近似总声级。最后，利用文献[6]对旋转叶片表面空化噪声的实验结果和文献[1-2]给出的部分潜艇螺旋桨空化噪声谱，整理得出了潜艇在任意航态下（无空化或者空化）整个频带内任意频率处的谱级计算式，并利用已有数据进行了检验，谱级相对误差小于3%。在空泡筒试验确定螺旋桨初生空泡数和判断潜艇用螺旋桨是否出现窄带"调"噪声后，利用本文所给表达式，可直接预测水面舰船和潜艇螺旋桨噪声谱级曲线。

2 螺旋桨噪声谱平坡形谱曲线特点

实船螺旋桨的水噪声，具有宽带谱的性质。实际测得的舰船螺旋桨噪声谱（包括空化与无空化），其频率是很丰富的，各个频率均有分量，一般在数百赫兹到若干千赫范围，是一种连续谱。并且，噪声谱虽然在各个频率处峰谷交替，但其总的趋势是从某一频率（f1≈200Hz）起，噪声谱级SL随着频率的增高而衰减。结合公开发表的美、英二战以后测得的螺旋桨噪声谱，可以认为螺旋桨噪声谱具有平坡形特性，即对于特定工况，由某一特征频率f1=（100～300）Hz起，噪声谱级SL以一定的斜率随频率的增大而降低，而在低于f1的频段，噪声谱级SL基本上是平的。该假定与国际海洋探测委员会（ICES）推荐的螺旋桨噪声标准一致。上世纪八十年代，法国Agosta-80潜艇在技术说明书中指出，其在航速Vs=3.5kns时（无空泡）螺旋桨噪声频谱级为SL=202.6-100/3·log f（f≥300Hz），如图1所示。图1表明，在特征频率f1=300Hz处，SL=120dB，300Hz以上频率，SL对应衰减率为-10dB/octave。二战时期美国Corvette护卫舰在航速Vs=15kns时（螺旋桨已出现空泡）螺旋桨噪声谱曲线如图2所示，其特征频率f1=100Hz，衰减斜率为-6dB/octave。桨噪声谱的平坡形谱曲线特征与螺旋桨发生空泡与否无关，但噪声谱级的高低和衰减斜率，却主要受制于空化情况。

谱强度随频率的平方增加而衰减，每一个倍频程噪声谱级下降约6dB[2]。实际测得的潜艇和某些水面舰船低速航行时，螺旋桨噪声谱以（-8～-10）dB/octave斜率随频率增加而衰减。当螺旋桨工作在非常恶劣的流场中时（如污底、严重空化），其噪声谱衰减斜率为其它值，但是，其噪声谱级SL与对数频率log f的关系都是接近直线。可推广得到声强一般表达式：dI=df，n为衰减指数。考虑一个倍频程频带，频率由f增加到2f，相应地其噪声谱级变化量为：

图1 Agosta-80潜艇航速Vs=3.5kns时噪声谱线Fig.1 Agosta-80 submarine noise spectra with the speed of 3.5 kns

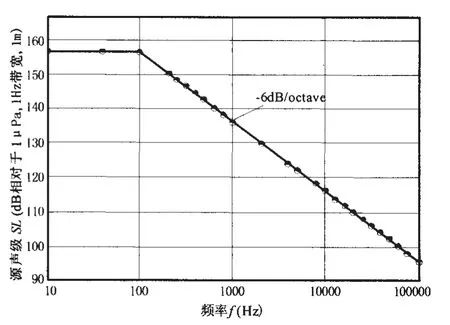
图2 Corvette护卫舰航速Vs=15kns时噪声谱线Fig.2 Corvette frigate cavitation spectra with the speed of 15kns

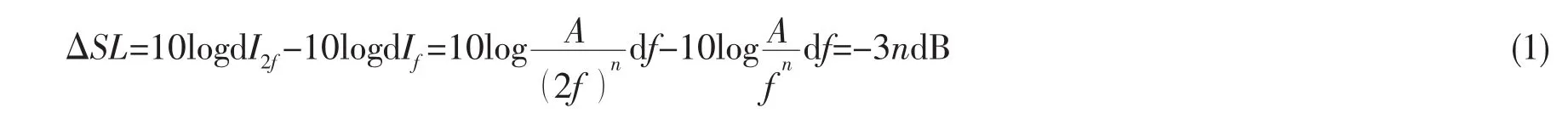
与文献[2]对应起来，当螺旋桨有空泡时，谱线衰减斜率-6dB/octave=-3ndB/octave，则指数n=2。依据实测值，在通常情况下，舰艇在无空泡低速航行工况时，其谱线衰减斜率为-10dB/octave（图1），则n=10/3。螺旋桨工作于特定恶劣工况时，衰减指数n为其他常数。

至于平坡形谱曲线的特征频率 f1及该频率处的噪声谱级SLf1=10logI0，与螺旋桨几何参数和运行工况有关，尚无法进行量化。文献[1]中给出：特征频率，其中s为桨叶截面弦长，p为局部压力，ρ为密度，σt为空泡数。峰值谱级SLf1=10logI0对应的声强B为发生空化的桨叶片数，r为观察点距声源距离，D为螺旋桨直径，U为叶梢周向速度，σti为初生空泡数。则可以得到：f1随螺旋桨线性尺度增加而降低，随沉深增加（压力增加）而上升，随航速增加而降低。随着螺旋桨直径增大、初生空泡数变大以及航速增加，谱级SLf1均表现为变大，并且在观察距离一定时，SLf1还与桨轴沉深和f1的大小有关。

螺旋桨空化依据空化产生位置的不同主要有：梢涡空化、毂涡空化和叶片表面空化（吸力面或者压力面）。叶片表面空化辐射噪声要比涡空化强，其中，吸力面空化是最强的噪声源，毂涡空化最弱[1]。螺旋桨工作时，叶梢局部合速度最大，梢部剖面最大厚度处压力最低，首先达到临界压力，最易产生空化，所以以叶梢空泡数来分析特征频率f1。

叶梢空泡数描述为：

其中，pa为水面大气压，H为叶梢距水面距离，pv为水的汽化压力，Vt为叶梢合速度，VA为螺旋桨进速，n为转速，为进速系数。螺旋桨通常工作范围为J=0.4～1.0，则可近似认为：螺旋桨空泡筒试验表明，在空泡可以被目测之前，即“可见空泡”出现之前，早已测得高频噪声讯号，即早已出现“声学空泡”。具体来说，对实船用螺旋桨，一般其初生空泡数σti＞2，但是一般在σt=4～5 时就已经出现空泡噪声了。 取 pa=101 325N/m2，g=9.8m/s2，pv=1 600N/m2（约 15℃），ρ=1 025kg/m3进行分析，水面舰船H≈1m，取空泡初生时σti≈2，由此得到：叶梢周向速度Ui≈10.35m/s。螺旋桨一般工作于 J=0.7～0.9，1-ω≈0.8，那么对应临界空泡数的航速（5.6～7.2 ） kn，由此证明了文献[2]中提出的水面舰船在通常航态下螺旋桨已充分空化的结论。

3 水面舰船螺旋桨噪声估算

如前所述，衰减指数为n的平坡形谱曲线在频带df内的声强的一般表达式为：

则df=1Hz的带宽内噪声谱在频率 f1和高频段内（f＞f1）任意频率f处的声强分别为：，对应的源声级谱级分别为：SLf1=10logI0=10logA-10nlog f1，SLf=10logIf=10logA-10nlog f，即可得到高频段内任意频率处的谱级为：

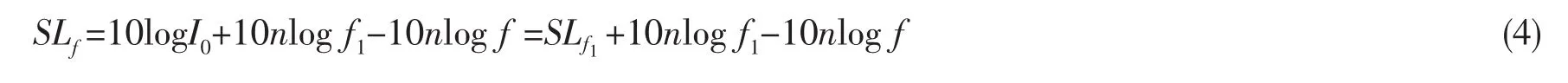
若给定带宽范围为 （fa,fb），则带宽内声强对应为：I=），总声强级为：

当 fa=f1， fb>>fa且 n≥2 时，得到高频段（f＞f1）的总声强级为：

可以看出：（4）式和（6）式计算均与特征频率f1和峰值谱级SLf1有关。依据前文分析，f1和SLf1均随航速而变化，即不同航速状态下对应的螺旋桨噪声谱线不同。

文献[5]给出了常见水面舰艇螺旋桨对应空化时噪声谱线开始以衰减指数n=2衰减的航速Vs1和对应空化充分发展到即将出现桨推力下降的航速Vs2的计算式，以及这两种航速下不同频段内噪声谱级的估算式。分别如下：

式中，A0为桨叶伸张面积，Ad为螺旋桨圆盘面积，A0/Ad即为螺旋桨盘面比，Kt为推力系数。仍然取J=0.7～0.9，H≈1m，由（7）式得 Vs1≈（6.4～8.1 ） kns，要比 Vsi大。

当航速Vs=Vs1时，谱级

当航速Vs=Vs2时，谱级

式中，Z 为桨叶数，kp为工作螺旋桨个数。在 f＞1kHz时，（9）、（10）式均对应为衰减指数 n=2，与前文一致，并且认为特征频率f1=100Hz。 对于频段 100Hz＜f＜1kHz，将频段 10～100Hz和 1～100kHz谱线光滑过渡连接即可，从而可以得到航速Vs1或Vs2下频段10Hz～100kHz内的空化噪声源声级谱线。当航速Vs1＜Vs＜Vs2时，给定频率 f，文献[5]建议可由Vs1对应的谱级SLfVs1和Vs2对应的谱级SLfVs2线性插值得到该频率处的谱级SLfVs：

到此即得到了水面舰船在螺旋桨发生空化后的任意可行航速下的噪声谱级预测图。由该理论预报模型得到某水面舰船螺旋桨空化噪声谱曲线如图3所示。 若需要得到高频段（f＞100Hz）的总声强级，因频段 100Hz＜f＜1kHz 的谱线衰减指数不确定，可近似也取为n=2，则由（6）式可估算得：SL100Hz→100kHz=SL100Hz+20。

4 潜艇螺旋桨噪声估算

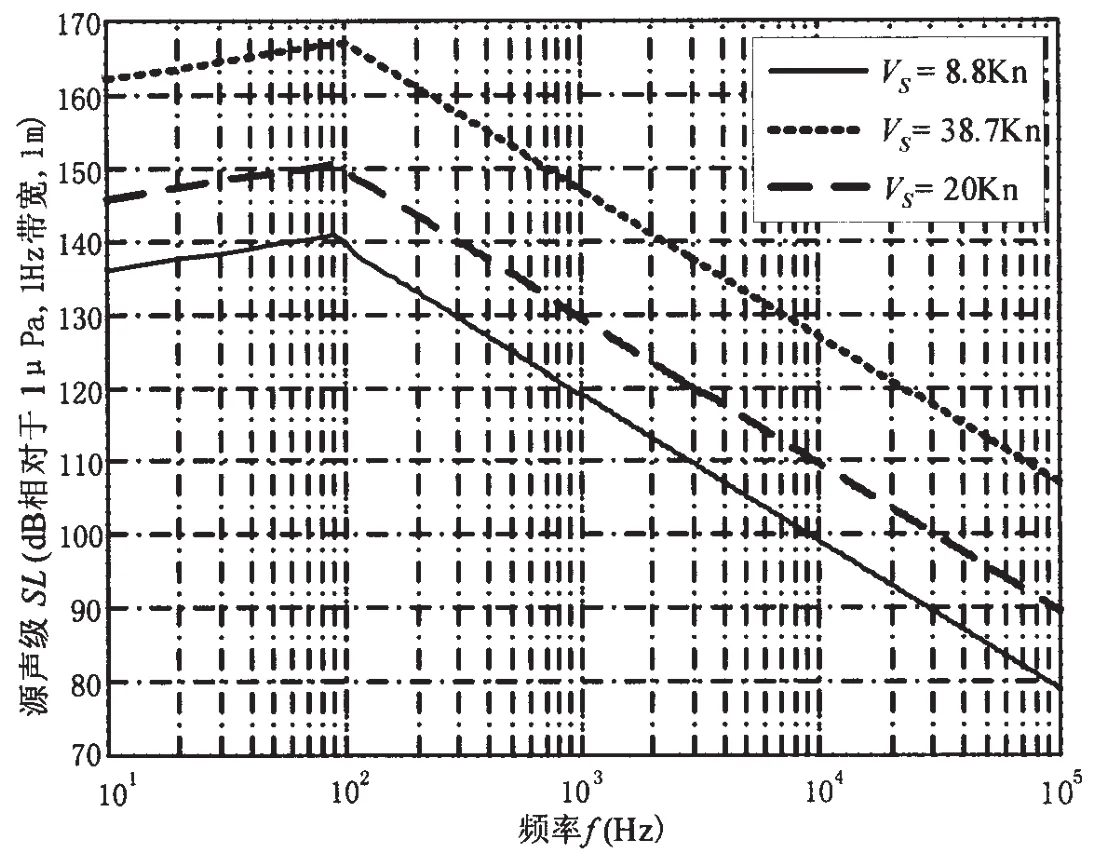
图3 某水面舰船螺旋桨空化噪声谱曲线理论预报Fig.3 Theoretically predicted ship propeller cavitation spectra with different speeds

在第2节中已提到，水面舰船对应空泡初生的临界航速约为（5.6～7.2）kns。而对于潜艇，通气管状态航行深度约为 18m（参照美国“Hake”号潜艇），螺旋桨工作范围一般为 J=0.5～0.8，若仍取 σti≈2，1-ω≈0.8，则同样可得到：Vsi≈（6.4～10.3）kns，当航行深度增加到 30m 时，该临界航速可达到约 14kns，而此时（6～14）kns范围正好对应于常规潜艇的通常航态，也就是说，潜艇也通常工作于螺旋桨空化初生状态或者是已经空化状态（σti=4）。为便于分析螺旋桨工作状态，取空泡初生时对应的转速Ni（rpm)进行分析，螺旋桨每个运行转数N对应一个工作状态。由（2）式可得：

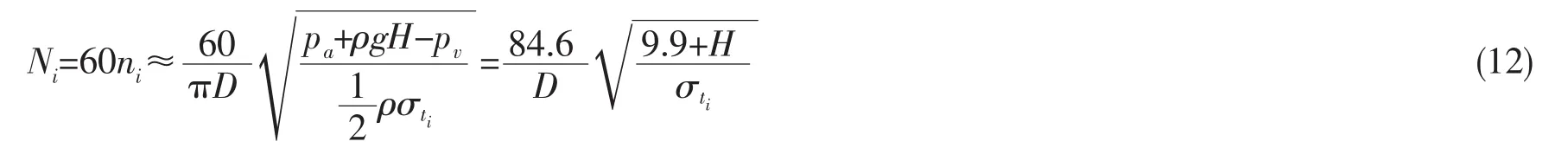
仍然在上述给定条件下，当D=2.5m，σti≈4时，Ni≈90rpm，即转数在超过约90rpm时，螺旋桨噪声谱级在约1kHz以上频段将按空化时对应的衰减指数n=2进行衰减。这里D和σti所取值均参照二战时美国USS-212型潜艇螺旋桨。

Lesnnovskii（1968）[6]对叶片表面空化噪声进行了深入的分析，σti≈1.9，得到谱级和总声级随相对转数N/Ni的变化如图4所示。总声级随转数升高分成明显的三个区域。在N/Ni=1.28～1.55区间，出现窄带“调”噪声，呈现一个尖锐的谱峰区，总声压级升高约6dB。转数升高时，高频段谱级先增加，尖锐谱峰区逐渐向低频段转移，转速达到约1.6Ni时，窄带“调”噪声消失。转速从Ni增加到1.28Ni，即从“声学空泡”产生到出现窄带“调”噪声，总声级升高约25dB。

图4 旋转叶片噪声谱级随相对转速的变化曲线[7]Fig.4 Noise spectra from rotating blades versus relative rotational speed,after Lesunovskii and Khokha(1968)

二战后公开发表的潜艇螺旋桨噪声系列测试，只有USS-212型潜艇的数据[1-2，8]。文献[1]中给出的美国USS-212型潜艇在不同转速下的螺旋桨空化噪声谱，如图5所示。其Ni≈90rpm，当N增加到110rpm时，对应为N/Ni≈1.22，刚好进入到图4对应划分的尖锐谱峰区。由上述分析，可近似取谱级增量为ΔSL≈25dB。再对应图4，转速110rpm谱线存在窄带调噪声，并且在频率f=5kHz处，相比于90rpm谱线的谱级增加量正好约为25dB，与图4对应起来。结合理想空化谱存在特征频率的特点，这里可将特征频率取为fm=5kHz，刚好对应为螺旋桨噪声主要高频段1～20kHz区间约为2octave中间频率处。

图5 美国USS-212型潜艇螺旋桨不同转数下噪声谱级[8]Fig.5 Measured cavitaion spectra of USS-212 submarine with different rotating speeds,after Strasberg and Sette(1944)

文献[2]中也同样给出了美国“Hake”号潜艇的空化噪声谱，且对应的转速值更多。当转数为170rpm时，约为1.9Ni，仍然存在窄带“调”噪声，由此可近似将尖锐谱峰区范围扩展为N/Ni≈（1.2，2.0）。由图5可知，在转数大于110rpm时，对应1～20kHz频段不同转数噪声谱线相互平行，均以约（-2～-3）dB/octave的斜率衰减，并且在同一频率处，谱级随转速增加近似呈等间隔分布。由此，可以利用线性拟合得到转数在N/Ni≈（1.2，2.0）范围内特征频率fm=5kHz处谱级SLfN的表达式：SLfN-SLf1.2Ni=13.75N/Ni-16.5。则在 fm=5kHz处，转数由 Ni增加到 N（1.2Ni＜N＜2.0Ni）时，谱级增加约（25+13.75N/Ni-16.5）dB。 同时，可由衰减斜率近似取衰减指数n=0.8，即平均衰减量约为2.4dB/octave。在确定了特征频率和衰减指数后，由（4）式即可求得对应图5中1～20kHz频段内任意频率处的噪声谱级，见（13）式，以及由（5）式可计算得到1～20kHz频段的总声级，见（14）式。

前文已提到，峰值谱级SLf1与螺旋桨直径、沉深、初生空泡数、航速（叶梢周向速度）以及特征频率有关。这里将特征频率取为5kHz后，在航行深度一定时，其噪声谱级SL5kHz将仍然与直径和航速有关。有学者根据收集到的一些潜艇螺旋桨在无空泡状态运行下对应同一个叶梢周向速度U=10m/s时的特征频率处谱级值SL5kHz，整理得到SL5kHz与螺旋桨直径D的单一函数关系：

同理，对于同一个螺旋桨，其直径一定，在频率一定时不同叶梢周向速度对应的噪声谱级也一定存在着某种转换关系。参照空泡数的定义式，对应压力系数Cp有：p-p0=CpρU2，p0为参考压力，即非定常流动引起的逾压 Δp可表示为：Δp=CpρU2=Cp′ρU2， 其产生的声压级为：40logU，由此可得叶梢周向速度由U1变为U2时引起的声压级增量近似为：

到此，由（15）式求得U1=10m/s时的特征频率处谱级后，再经（16）式转换可得到所求航速（转速）下特征频率对应的噪声谱级为：

再由（13）式即可得出无空泡状态下高频段内任意频率处的谱级值。但是，因为（15）式是在无空泡状态下得出的表达式，依据前文分析，转数由Ni增加到N（1.2Ni＜N＜2.0Ni），即空泡产生时，fm=5kHz处谱级增加约为（25+13.75N/Ni-16.5）dB，所以螺旋桨在空泡状态下运行时，特征频率处谱级应表达为：同样再代入（13）式即可得到空化状态下高频段内任意频率处的谱级值。

以图5中转速为130rpm航态来检验上述计算式是否准确。N/Ni≈1.44，出现空泡。 由（14）式得 SL5kHz10m/s≈76dB。 U=17m/s， 则SL=76+40log+25+13.75×1.44-5kHz16.5≈113.5dB，再由（13）式可得到：SL2kHz=113.5+8log5 000-8log2 000=116.7dB，SL10kHz=111.1dB。查图 5，2kHz、5kHz和 10kHz处谱级分别约为113dB、111dB和109dB，误差均小于4dB，说明上述计算式可以用来进行粗略估算。由上述理论预报模型对法国Agosta-80潜艇噪声谱级计算如图6所示，3.5Kn时计算值较技术说明书数据低，可能是厂方留有裕度。

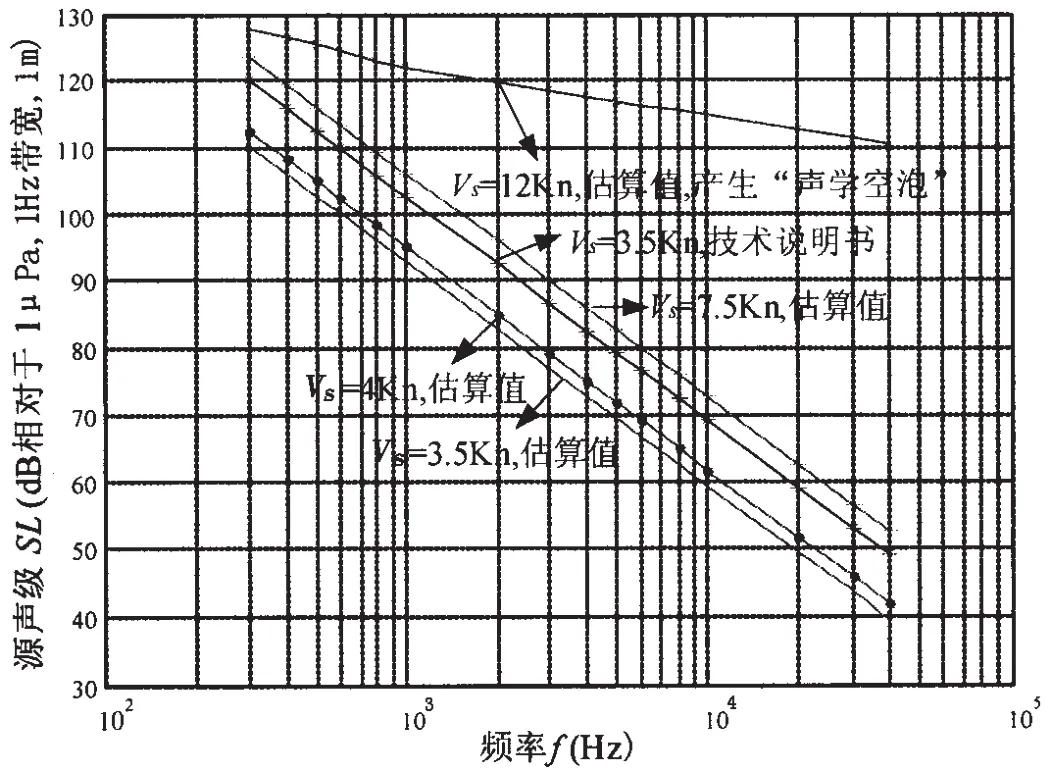
图6 法国Agosta-80潜艇螺旋桨噪声谱级理论预报Fig.6 Theoretically predicted propeller noise spectra of France Agosta-80 submarine with different speeds

再考虑低频段 100Hz～1kHz。由（13）式得到 1kHz处谱级为：SL1kHz=SL5kHz+5.6，若将（4）式由高频段推广到频段100Hz～1kHz，那么可得到该频段内任意频率处噪声谱级为：

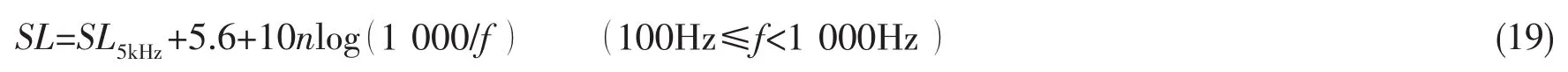
（19）式中n可理解为平均衰减指数。从理论上讲，可以先由图5中每一个转数的噪声谱曲线得出十频程100Hz～1kHz内的谱级衰减量，对应一个衰减指数n，再进行线性拟合，即可得到任意转速下的谱线衰减指数，代入（19）式，即可确定低频段内任意频率处的谱级。但是这里因为图5中给出的不同航态很少，拟合得到的n值可能误差很大，所以没有给出转数N与衰减指数n的关系式。

最后，分析（17）式，只是表述了转速在尖锐谱峰区内时特征频率fm=5kHz处的谱级增加量，而对于出现在低频段100Hz～1kHz内的窄带“调”噪声中心频率ftonal和峰值谱级SLftonal并不能得到。再次分析图5，转速为110rpm、130rpm和160rpm所对应的调噪声谱级峰值相对于不存在窄带调噪声时该中心频率处的谱级增加量均约为15dB，见图5所示，可认为其具有一般规律。对于频率ftonal，文献[6]给出其近似的1/3倍频程：

其中，Z为螺旋桨桨叶数。由ftonal和该频率处的谱级增加量即可确定该1/3倍频程内的调噪声谱曲线。至此，结合（16）、（17）、（13）、（18）式和（20）式即得到了潜艇在任意航态下整个频带范围（100Hz～20kHz）内的螺旋桨噪声谱曲线。

5 结 论

螺旋桨空化噪声是最主要的舰艇辐射水噪声源。水面舰船在通常航态下螺旋桨已充分空化。螺旋桨空化初生时对应的临界航速也正好是潜艇的通常航态。确定螺旋桨噪声平坡形谱线的关键在于特征频率、峰值谱级以及谱线衰减指数的确定。利用平坡形谱曲线在高频段微小频带内声强的一般表达式可推广得到整个频段内（～100Hz-40kHz）任意频率处的谱级表达式以及频带级。利用水面舰船螺旋桨空化状态下两个特征航速对应的部分频段内的噪声谱级计算式，可拟合得到螺旋桨发生空化后任意可行航速下的噪声谱曲线图。对于潜艇螺旋桨噪声谱级，在无空化状态下，可结合叶梢周向速度一定时特征频率处谱级与直径的单参数函数关系和频率一定时叶梢周向速度变化引起的特征频率处谱级的变化量得到特征频率处谱级，进而得到频段内任意频率下的谱级；而在空化状态下，特征频率处谱级还需要加上由于进入尖锐谱峰区和转速进一步增加引起的声级增量。计算中用到的初生空泡数大小和在一定转速下潜艇螺旋桨是否会出现窄带“调”噪声要通过空泡筒试验进行确定。

[1]Ross D.Mechanics of underwater noise[M].Pergamon Press,New York,1976.

[2]Urick R I.Principle of underwater noise[M].McGraw-Hill,New York,1981.

[3]朱锡清,唐登海,孙红星等.船舶螺旋桨低频噪声研究[J].水动力学研究与进展,2000,15(1):74-81.

[4]孙红星,朱锡清.螺旋桨离散谱噪声计算研究[J].船舶力学,2003,7(4):105-109.

[5] Издателъство.Справочиник по теории корабля[M].Ленинград,1986.

[6]Lesnnovskii V P,Khokha Y V.Characteristics of the noise spectrum of hydrodynamic cavitation of rotating bars in water[J].Sov.Phys.-Acoustics,1968,14:474-478.

[7]Boguslavskii Y Y,Korets V L.Cavitation threshold frequency dependence[J].Sov.Phys.-Acoustics,1966,12:364-368.

[8]Strasberg M,Sette W J.Measurement of propeller noise on three submarines of the SS 212 class[R].D.T.M.B.Rept.R-205,1944.