振荡水柱波能发电装置气室的三维数值模拟研究＊

纪君娜,刘 臻,纪立强

(1.中国海洋大学工程学院,山东青岛 266100;2.胶东调水局青岛分局棘洪滩水库管理处,山东青岛 266111;3.中交烟台环保疏浚有限公司,山东烟台 266100)

我国作为有着漫长海岸线的海洋资源大国,在利用开发海洋能源,特别是海洋波浪能方面具有先天优势。波浪能的分布广泛,能量密度高,波浪能发电多是在沿岸和海上进行,因此不占用土地,不需要迁移人口,且具有综合利用效益,多年来一直是海洋可再生能源中的开发热点。

目前,振荡水柱波能发电装置是实用化与商业化开发程度最高的波浪能转换装置之一。该类装置主要由气室、输气管道、空气透平与发电机组构成。气室为一半淹没空仓结构,仓室前墙下部开敞,入射波浪将带动气室内的水柱做上下振荡,并带动水体上部的空气通过输气管道与外界大气之间做往复运动,称为能量一次转换过程。空气驱动透平电机转动,便可实现波浪能向电能的转换,称为能量二次转换过程。其中,气室是实现能量一次转换过程的主要结构。

随着对波能发电装置重视程度的日益增加及研究手段的愈加丰富,国内外学者对气室和能量一次转换过程等相关问题进行了广泛而深入的研究。刘月琴等[1]对传统岸式振荡水柱波能装置的气室部分进行了实验研究,重点考察了海岸岸坡之间的效应关系及其规律。当入射波周期较大时,海岸岸坡对振荡水柱的垂向运动响应影响不大,但对吸能效率和单位宽度波能俘获率的影响较为明显。梁贤光等[2]在造波水槽中进行了汕尾100kW 波力电站气室模型的性能试验。气室的波能转换效率不仅随波周期变化,而且随波高而异。试验还表明,气室的形状对波能转换率的影响也较大。Brito-Melo[3]用直接计算方法预测振荡水柱装置的水动力特性,为求解气室内压力分布,他们改进了气室内自由水面处的动力学边界条件,同时利用压力辐射法计算气室内往复气流的压力。计算结果证明边界元方法能够有效地计算波浪的绕射和衍射问题。Lew is&Delaure[4]提出一种计算岸式振荡水柱系统的数值模型,利用一阶混合面元法求解在定常边界条件下规则波与波能装置的相互作用。对规则波与不规则波的计算与实验结果的对比,验证了该模型的可靠性。

本研究构建了基于计算流体力学软件Fluent的三维数值波浪水槽,用以研究气室前的波浪传播与气室内的水面振荡变化。该数值波浪水槽的控制方程为连续方程和基于雷诺平均的纳维尔斯托克斯方程,自由水面的重构方法为VOF法。通过与试验数据的对比,验证了本研究构建方法的准确性及在相关研究中应用的可能性。

1 三维数值波浪水槽

1.1 控制方程

三维数值波浪水槽造波板位于水槽的左侧,开边界则位于水槽的右侧(图1)。该水槽的数值波浪水槽分别为控制方程和基于雷诺平均的纳维尔斯托克斯(RANS)方程：

图1 三维数值波浪水槽示意图Fig.1 Sketch for a 3D numericalw ave tank

式中,t为时间;xi,xj和ui,uj为x,z方向的坐标向量和对应的速度分量;ρ,p,ν和 fxi为流体的密度、流体的压力、运动粘性常数和体积力。

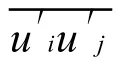
自由水面的追踪与重构采用H irt&Nichols提出的流体体积分数法,简称VOF方法[5]。该方法假设在某一计算单元内水相所占体积与气相所占体积的总和为定值,水相的计算公式如下：

式中,aw为水相体积分数;t为时间。此外,水气界面重构与通量计算通过由Youngs在1982年提出的假设单元内的线性斜坡的方法获得[6]。

1.2 数值方法

为了更好的揭示振荡水柱波能发电装置的工作机理,主要采用规则入射波进行研究。造波方法为推板式,数值波浪水槽的开边界条件则采用Sommerfield辐射边界条件,该方法已经被证明对规则波的吸收较好。

造波与消波边界的功能主要通过Fluent软件的用户自定义(UDF)函数实现,计算程序中的动网格运动则采用边界铺层的方法。计算网格则由Gambit 2.0生成,并在水气交界面处进行了加密。

控制方程的数值求解方法采用有限体积法,对流项的求解则为二阶迎风格式。速度压力耦合使用“含有分裂算子压力隐式的非迭代时间步进(NITA-PISO)”方法。上述方法与VOF法相兼容,且能够显著降低计算耗时。

2 振荡水柱波能装置的气室结构

振荡水柱波能发电装置前方的波浪传播、气室内的自由水面振荡及输气管内的往复气流的运动都受到气室形状的影响。因此,气室及其相关参量在能量一次转换过程中具有重要作用。开展针对气室形状参量的研究,对揭示振荡水柱波能装置的工作机理、提高气室工作性能将有较高的工程意义和实用价值。

本研究所采用的气室主要的气室形状参量包括：气室宽度lf;气室前墙吃水深度ds;气室内静水面上高度lh;气室前墙厚度ls;气室顶部开口宽度ld,底坡水平长度lm;底坡坡角θs;气室墙前平均水深h。若ld=lf,则代表气室为完全开敞,否则为部分开敞。圆柱形输气管安装在气室的顶部中央位置,输气管的直径为ld,高度为hd(图2)。

为了考察振荡水柱波能装置结构对气室工作性能的影响、验证所构建三维数值波浪水槽的准确性,研究计算了不同的气室结构参量(表1)。除表中的形状参量之外,输气管的高度hd=13.2 m,底坡水平长度lm=22.86m,底坡坡角θs=26°,气室的墙前平均水深为16m。此外,本研究采用的入射波高度为1m,入射波周期为3.5～8.0 s。

图2 振荡水柱波能装置气室结构示意图Fig.2 Sketch showing the air chamber in a OWC wave energy convertor

表1 不同试验工况条件下的形状参量(m)Table 1 Experimental cases with various shape parameters(m)

3 数值模拟结果与讨论

工况1～3中,在不同入射波周期条件下气室内波面生成变化特征相似(表1),以工况2入射波周期 T=5.5 s时气室内的波面升沉变化为例。如图3a所示,当振荡水柱的波面达到波峰时,气室内各点处的波面高程并不相等：气室前墙及后墙附近的波面高程大于中部,但前墙与后墙附近的波面达到最高的时刻不同。前、后墙两位置处的波面高程平均值约等于气室中部的高程值。由图3b可见,气室内振荡水柱达到波谷时,其自由水面的运动特征与其到达波峰时的规律基本相同,即气室内自由水面高程分布沿入射波方向存在区别,而在垂直于入射波方向上波面高程的分布差别不大。

相对波幅指气室内的振荡波幅(a)与入射波幅(a0)的比值,反映了气室内水面振荡的幅度和剧烈程度。当气室内的波幅较大时,振荡水柱将推动更多的空气在输气管内做往复运动,意味着更多的波浪能量可以在能量一次转换的过程中变为空气能量。因此,气室内的相对波幅可以较为准确的反应该装置工作性能的优劣。由图4可见工况2条件下,入射波周期为T=5.5 s时气室中部自由水面相对波幅的变化情况。气室中自由水面的摆式振荡造成波幅升沉运动不再呈正弦变化。此外,自由水面振荡的周期与入射波周期基本相同,且入射波幅有明显的提高。

各工况条件下的振荡水柱波能发电装置气室内中部的自由水面相对振幅三维数值模拟计算结果如图5所示。为更好的验证计算结果,本研究与Zhen Liou[7]等二维数值模拟计算也进行了比较。从总体上看,三维数值模拟结果与试验数据较为吻合;在长周期区,三维数值计算的结果与试验数值更为符合,优于刘月琴[2]中的二维数值模拟计算结果,但仍小于试验值,这是由于相对于二维计算,三维数值模拟能够更好的处理和垂直于入射波向的波面分布情况及其对气室中部的影响。

从总体上看,本研究各形状参量条件下的相对波幅沿入射波周期的分布规律基本相同。在短周期区(T=3.5～6.0 s),气室内的相对波幅随着周期的增加而增加。在长周期区(T=6.0～8.0 s),气室内的相对波幅则随着周期的增加而趋于一个较为稳定的数值,相对波幅在2.0左右。由此可见,在进行波浪能装置运行的选址过程中,应尽量选择实海况平均周期大于6.0 s的海域。在上述条件下,波能能量的转换效率较高,且装置的工作性能也较高。

图3 三维振荡水柱波能装置气室内水面升沉变化Fig.3 3D view for the up and dow nmovementof the free surface in the chamber of the OWCw ave-pow er convertor

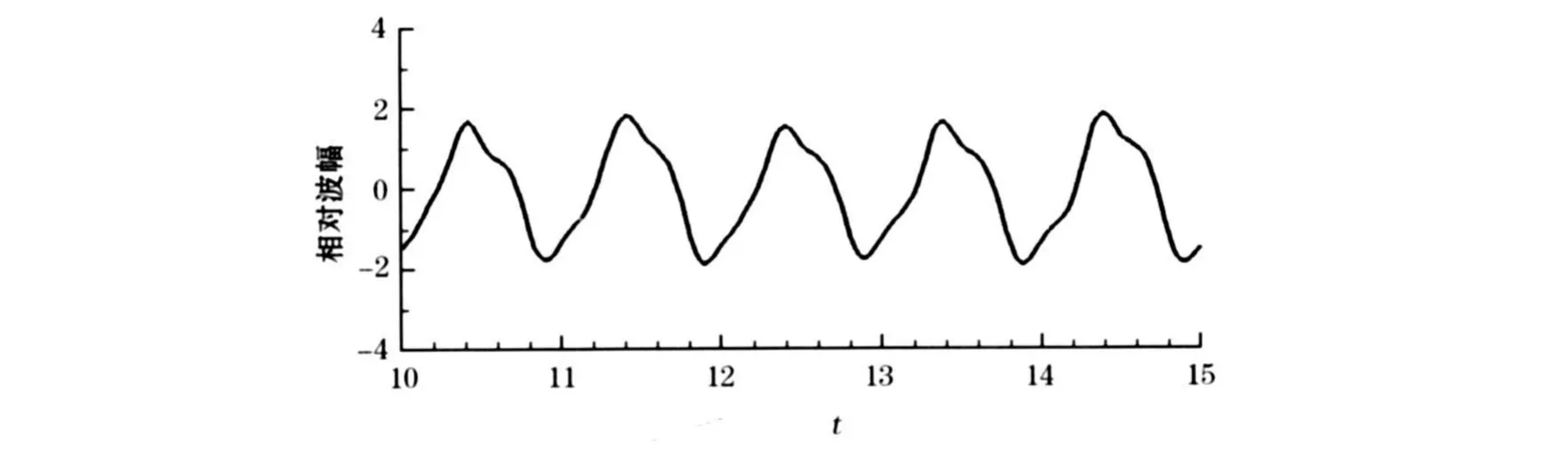
图4 三维振荡水柱波能装置气室中部相对波幅时程曲线Fig.4 Time Series of relative amplitude at them idd le of the chamber in the 3D OWC w ave-power convertor

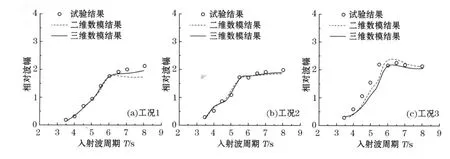
图5 振荡水柱波能装置相对波幅的计算比较Fig.5 Comparison among the results respectively from the calculations of relative wave am plitude for a OWC w ave-pow er convertor

4 结 语

本研究构建了基于计算流体力学软件Fluent的三维数值波浪水槽。该数值水槽的控制方程为连续方程和RANS方程,自由水面追踪与重建则采用PLIC-VOF方法,并将上述数值计算模型成功应用于振荡水柱波能发电装置气室内水面振荡变化的研究中。

计算结果表明,本研究的数值模拟结果与试验数据较为吻合,且优于文献中的二维数值计算方法。因此,可被用于该领域内相关问题的研究。此外,振荡水柱波能发电装置的气室结构在长周期区(T=6.0～8.0 s)条件下的工作性能较好,能量转换效率较高。气室前墙吃水与输气管径则对自由水面的振荡的影响较小。

[1] 刘月琴,武强.岸式波力发电装置水动力性能试验研究[J].海洋工程,2002,20(4)：93-97.

[2] 梁贤光,孙培亚,游亚戈.汕尾100kW 波力电站气室模型性能试验[J].海洋工程,2003,21(1)：113-116.

[3] BRITO-MELO A,SARMENTO A JN A,CLE′MENT A H,et al.A 3D boundary element code for analysis o f OWCw ave-pow er p lants[C]∥Proceedings of the Ninth International Offshore and Po lar Engineering Conference.Brest：[s.n.],1999：188-195.

[4] DELAURE Y M C,LEW ISA.3D hydrodynamicmodeling of fixed oscillating w ater column w ave pow er p lant by a boundary elementmethod[J].Ocean Engineering,2003,30(3)：309-330.

[5] H IRT C W,N ICHOLS B D.Vo lume of fluid(VOF)method for the dynam ics o f free boundary[J].Journalof Computational Physics,1981,39(1)：201-225.

[6] YOUNGS D L.Time-dependentmu lti-material flow with large fluid distortion[J].Numerical Methods for Fluid Dynam ics,1982,22(1)：273-285.

[7] LIU Z,JIN J Y.Numerical analysis o f wave field in OWC chamber using VOFmodel[J].Journal of Ocean Technology and Engineering,2008,22(2)：1-6.