桩列透空堤的水动力计算＊

朱大同,傅朝方

(1.东南大学江苏省工程力学重点试验室,江苏南京 210096;2.东南大学土木工程学院,江苏南京 210096;3.南京水利科学研究院河流与海岸研究所,江苏南京 210024;4.东南大学华宁交通监理咨询公司,江苏南京 210018)

随着海岸带深度开发和港口工程的快速发展,各种类型的防浪与消波透空结构得到普遍重视[1-3]。矩形桩列组成的防波堤是软土地基上常见的透空堤,由于它能防护波浪对海岸和港口的冲击,又能透流,保持港内水体循环,维护水体质量和生态环境,所以在我国己被广泛应用,并列入防波堤设计与施工规范[4]。但至今没有合理的水动力理论公式可供工程应用。Hagiwara,Isaacson等和Kakuno等[5-7]对桩列防波堤的反射、传递系数和波浪力展开了理论和试验研究。我们通过阻抗分析法[8-9]讨论矩形桩列防波堤的水动力学特征,得到一组理论公式,可以方便地计算波浪反射、传递系数和波浪力。

1 矩形桩列防波堤水动力学特征的阻抗分析

计算图式和坐标轴取法如图1。桩列由若干个宽度为b,厚度为δ的矩形柱组成。桩间净距为2a。坐标轴放在静水面上,原点在堤中心,x轴指向来波方向,y轴与桩列轴线重合,z轴垂直向上。水深d,波高h,周期T的推进波正向入射到堤面上。设定堤厚度δ与港池相比是一个很小的量。将总的流场分为两个子域：港池外海域(x≥0)和港池内域(0≥x)。

1.1 桩列上力平衡方程和阻抗公式

法向入射波(波向与x轴平行)在桩列迎海面单位宽度上的波浪力为Fo0,传递波在桩列背海面上的波压力和在x方向水质点的速度分别为PT0和VT0,桩列的流阻为R0。桩列上力平衡方程有如下形式：

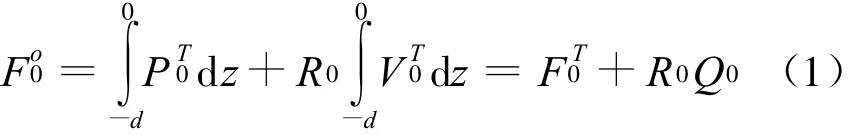
式中,FT0为桩列背海面单位宽度上的波浪力;Q0为通过桩列的体积流量。

按阻抗率定义[8]和式(1),桩列迎海面上的阻抗率是：

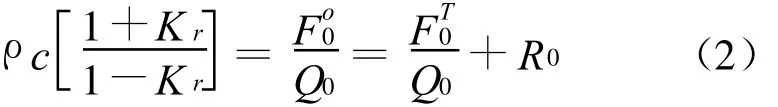
式中,ρ,с分别为水的密度和波的相速度,两者乘积称为特性阻抗;K r是反射系数。式(2)中右端两项(港池内传递波的阻抗率和桩列的流阻)可用下面方法确定。

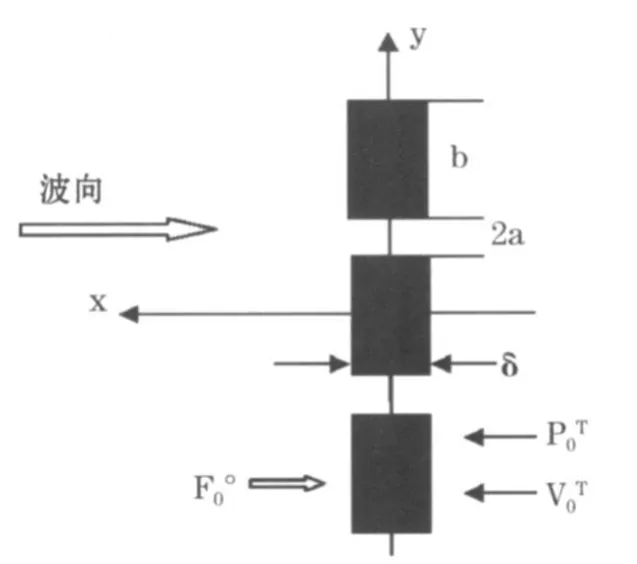
图1 桩列透空堤顶视图Fig.1 A top view over the pile-permeable dike

1.2 港池内传递波的速度势

港池内传递波的速度势、水质点在x方向速度和水波压力有：

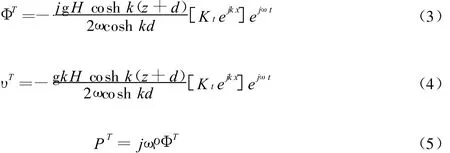
式中,k、g和ω分别为波数、重力加速度和波圆频率;Kt为传递系数。

在式(4)和(5)中取x=0,并沿水深积分,于是式(2)右端第一项可表为：

式(6)表明,传递波在常水深港池内传播时阻抗是匹配的。

1.3 外部海域中波的速度势

入射波的速度势：

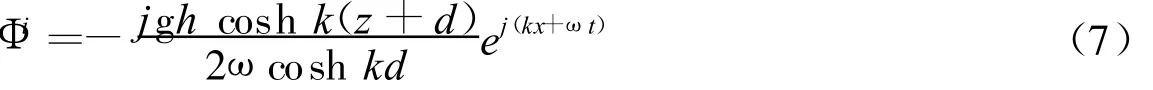
法向入射波与反射波迭加后波场的速度势为：

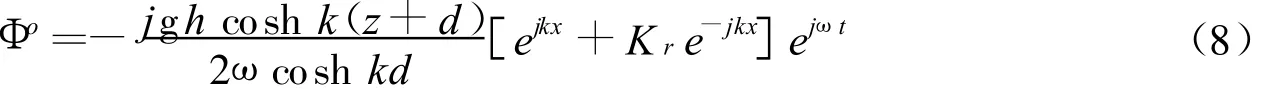
1.4 桩列流阻分析

水波通过桩列的压力损失可表为[9]：

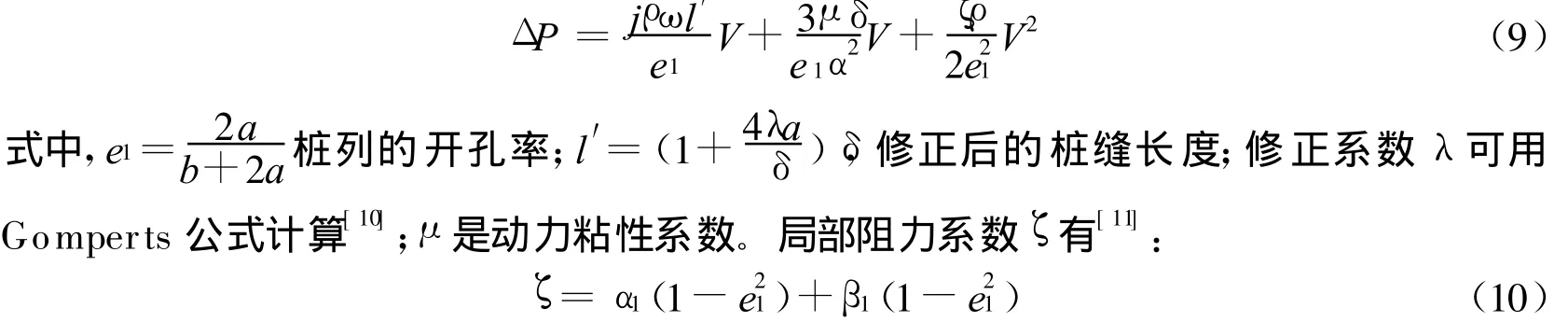
对于尖棱直角α1=0.75,β1=0.4;对于圆弧或缓变α1=0.5,β1=0.2。于是桩列的非静态流阻R0为：

式中,vn为速度的幅值,并且沿水深取平均值,得：

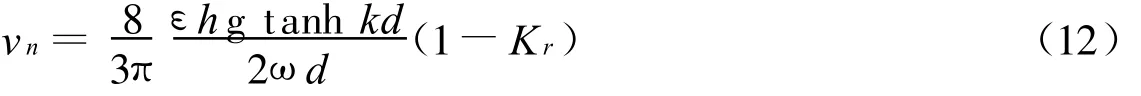
按文献[9],对于浅水波和相对浅水波(kd≤0.7),有：

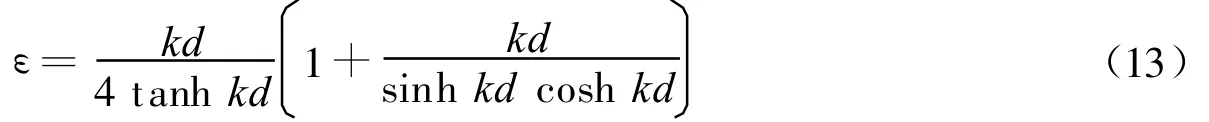
对于中等水深波和相对深水波,有：

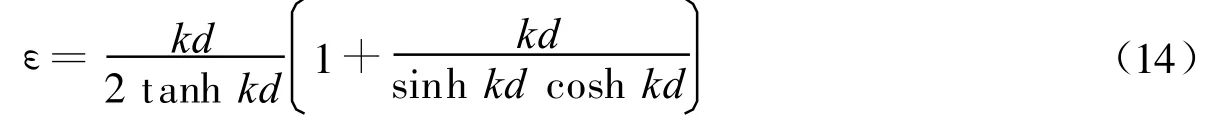
2 桩列防波堤的波浪反射和传递系数计算公式

2.1 波浪反射系数公式

将式(6)和(11)代入式(2),经整理得波浪反射系数计算公式：

2.2 波浪传递系数公式

波浪从矩形桩列上传递系数的公式如下：

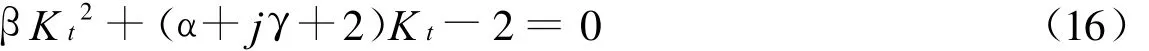
3 桩列上波浪荷载计算公式

在x=0断面处,单位宽度(b+2a)上入射波波浪力可由式(7)得到：

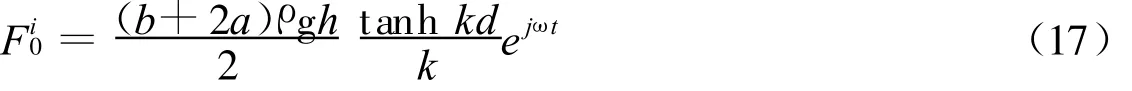
桩列迎海面单位宽度(b+2a)上,入射波和反射波波浪力可由式(8)得到：

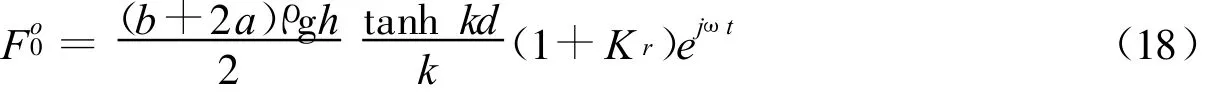
桩列背海面单位宽度(b+2a)上传递波波浪力可由式(5)得到：

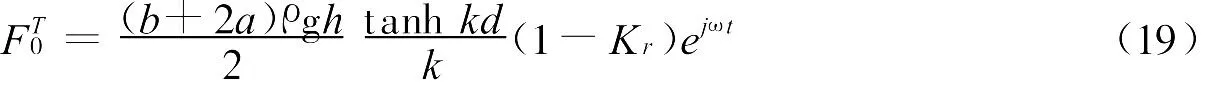
于是,桩列单位宽度(b+2a)上净波浪力为：

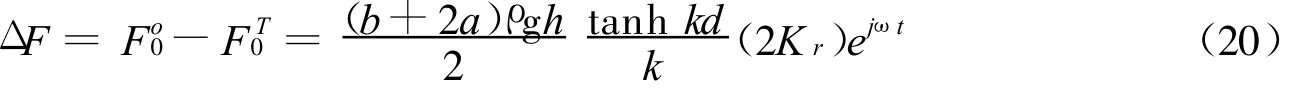
式(17)与式(20)之比为桩列上净波浪力的传递函数：

4 对比验证

对于海况条件和结构参数已经确定的桩列防波堤,在式(15),(16)和(21)内需用的数据已齐全,没有待定或要预先从模型试验反算的参数。由于公式结构十分简单,数据均是现成可查,所以计算工作非常方便。

现将文中的理论公式与文献[5]～文献[7]中试验成果对比。

4.1 计算的反射系数和传递系数与试验数据比较

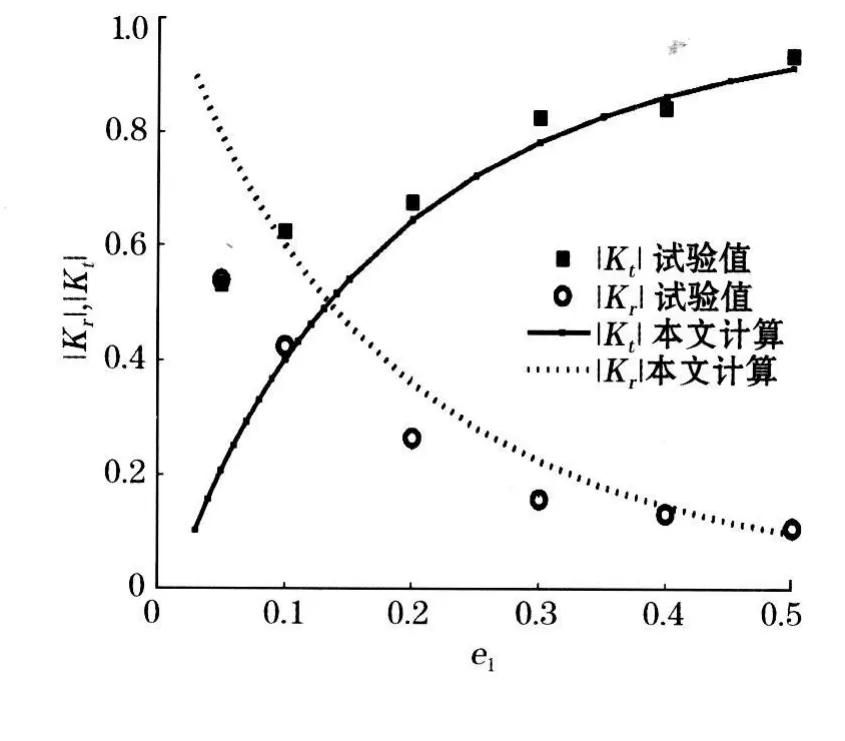
图 2 预测值|K t|和|K r|与试验值[6]比较Fig.2 Com parisons respectively between the predicted|Kt|and the|K t|from experiment,and betw een the p redicted|K r|and the|K r|from experiment

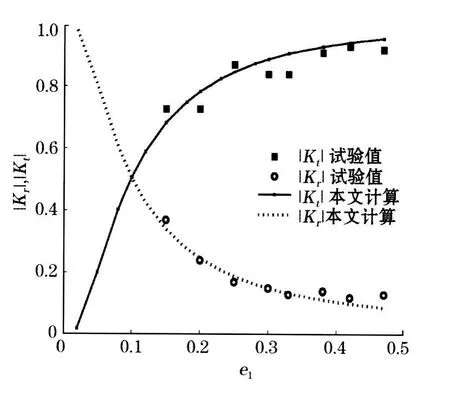
图3 预测值|K t|和|K r|与试验值[5]比较Fig.3 Comparisons respectively between the predicted|K t|and the|K t|from experiment,and between the p redicted|K r|and the|K r|from experiment

比较结果列于图2和图3上。图2是计算值与Isaacson等[6]试验对比。计算中按文献[6],附加质量的影响不考虑,即取λ(以后同)。式(11)中右端第一项是感抗,在电磁波或声学理论中,只有在发生共振和高频振动时重要,低频段通常可略去。但是在分析水波与单层透空结构相互作用(不会发生共振)时不能忽视。图示曲线表明,无论是反射系数还是传递系数,计算值与试验吻合较好。图3是反射和传递系数计算值与Hagiwara[5]试验对比,计算值与试验值一致。

4.2 计算波浪力与试验数据的比较

由于Kakuno等[7]用二倍的入射波波浪力与桩列上净波浪力做对比,所以式(21)应改写为：

图4是波浪力预测值与Uda等[7]试验结果对比。Uda等的试验是在相对浅水条件下进行,因此,用对应的理论公式(13)和(22)计算。图示曲线表明,计算与试验非常吻合。

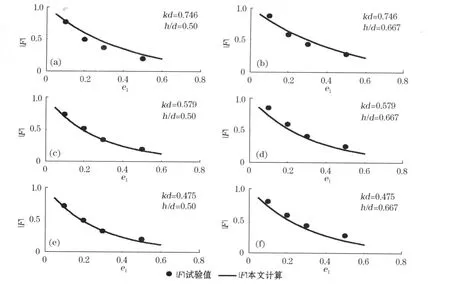
图4 预测值|F|与试验值[7]比较Fig.4 Comparison betw een the predicted|F|and the|F|from experiment[7]

Kakuno等[7]波浪力试验值与本文的理论予测吻合也很好(图5)。

5 结 语

文内导出的反射、传递系数和波浪力计算公式,简单严密,计算精度优良,便于工程应用。桩列透空堤有较好的应用前景,但它对长周期波的消减作用很小。为适应特定频段内的波浪作用,可用多列桩配以不同的间距,组成具有带通特征的滤波器,可以发挥更好的防浪消波作用。

本研究获得进一步发展的阻抗法,是一个适应性强的解析方法,它还可应用于水波与其它结构相互作用。

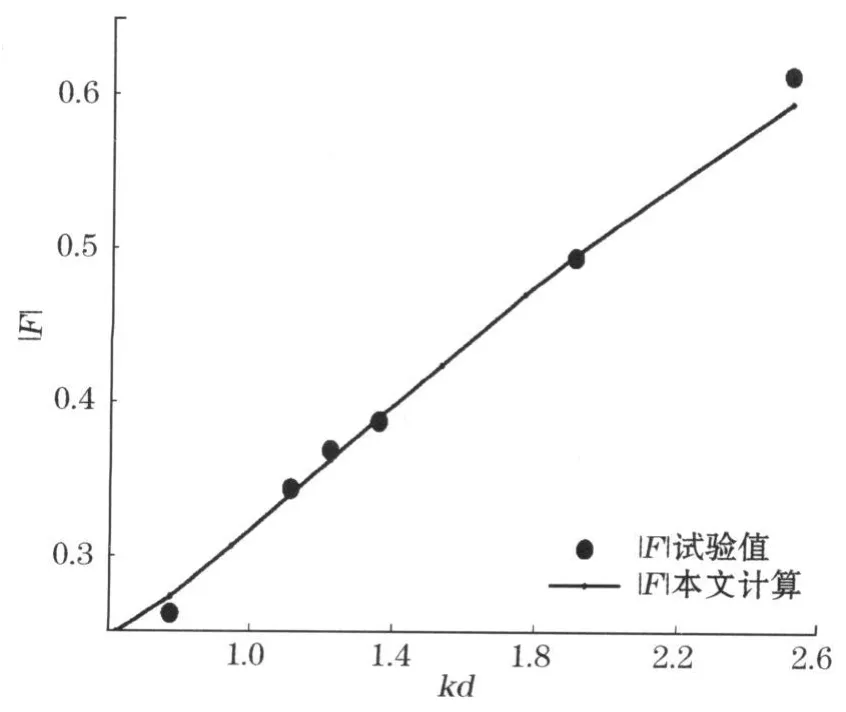
图5 预测值|F|与试验值[7]比较Fig.5 Comparison between the predicted|F|and the|F|from experiment[7]

[1] 候国本.管式透空防波堤试验研究[J].海岸工程,1982,1(1)：1-8.

[2] 贾玉成.挡板式高桩码头透浪特性分析[J].海岸工程,2009,28(1)：1-8.

[3] 龚崇准,陈美发,朱宪伟,等.桩式离岸堤保滩促淤工程消浪效果试验研究[J].海洋工程,2001,19(4)：72-77.

[4] JTJ298-98防波堤设计和施工规范[S].北京：人民交通出版社,1998.

[5] HAGIW ARA K.Analysis of up right structure for wave dissipation using integral equation[R].Proc.19th Int.Conf.on Coastal Engineering(ICCE),H ouston：ASCE,1984：2810-2826.

[6] ISAACSON M,PRENASURIS,YANG G.W ave interactions with vertica l slotted barrier[J].Waterw ay,Port Coast,and Ocean Engineering,1998,124(3)：118-126.

[7] KAKUNO S,NAKATA Y,LIU P L-F.Wave forces on an array o f vertica l cylinders[J].W aterway,Port,Coast,and Ocean Engineering,1996,122(3)：147-149.

[8] ZHU D T,ZHU SW.Impedanceanalysis of hyd rodynam ic behaviors for a perforated-wall caisson breakwater under regular wave orthogonal attack[J].Coastal Engineering,2010,57(8)：722-731.

[9] ZHU D T.Impedance Analy ticalMethod o fw ave run-up and ref lection from a slotted-wall caisson breakwater[J].China Ocean engineering,2010,24(3)：453-465.

[10]GOMPERTSM C.The sound insulation of circular and slit-shaped apertures[J].A custica,1964,14：10-16.

[11]吴持恭.水力学[M].北京：高等教育出版社,1987.