基于霍普金森压杆系统的动态压痕实验*
2011-02-26李玉龙
张 新,候 兵,李玉龙
(西北工业大学航空学院,陕西 西安710072)
压痕硬度实验是一种应用广泛的材料性能测试技术,主要思想是强制压迫“较硬”的压头进入“较软”材料的表面,通过记录压入过程中载荷和压痕深度的关系曲线,研究材料抵抗外物侵入的能力,即材料硬度[1]。压痕法具有成本低、损耗小、使用简便、试样加工方便等优点。在压痕实验中,变形主要集中在压痕附近区域,使得该方法与传统单轴压缩或拉伸等测试技术相比,具有复杂的2D/3D 变形效应,然而鉴于该方法本身特有的简易性,仍有大量理论、实验和数值计算等研究工作致力于发展其在材料性能测试方面的应用[2-3]。然而已有的研究[4]表明,许多金属材料在高应变率下表现出明显区别于静态加载的变形特性,如屈服和流动应力提高,断裂韧性增大,绝热温升显著等[5-8]。若将静态压痕实验技术直接拓展用于研究材料动态性能,可能会出现较大偏差,因此有必要发展动态压痕实验技术,研究材料硬度对加载速率的敏感性,以期得到一种新的材料率敏感性研究方法。
早期的动态压痕实验技术基于落重实验和“回弹技术”[9-11],这种方法不仅增加了数据处理的复杂性,也因数据处理方法的差异无法与静态硬度实验结果进行对比。Y.Tirupataiah 等[12]用气枪冲击球形压头的方法设计了一种动态压痕实验,研究了平均应变、平均应变率与流动应力或动态硬度之间的关系,铜和钢的变形应变率在103~104s-1之间。J.P.Nobre 等[13]发展了一种基于摆锤装置的动态压痕技术,通过在摆锤后部安置压电传感器,测量压痕过程中的冲击载荷信号,可以得到应变率为102s-1量级的材料动态硬度。J.Lu 等[14]的动态压痕装置使用了光学干涉测量方法,测量压深-时间曲线,弥补了之前动态压痕实验中无法测量这一重要物理量的不足。
Hopkinson 装置是目前较为常用的材料动态性能测试方法,由于在加载方式和测量精度方面相对于其他动态测试技术具有显著优势,一些学者也曾试图进行改造用以进行动态压痕实验。文献[15-17]中利用Hopkinson 杆的宽幅应力脉冲加载技术和子弹撞击入射杆产生的应力脉冲,通过安置在入射杆另一端的压头直接撞击固定在支座上的试样加载;该装置分别采用了安置在试样和支座之间的载荷传感器和压头附近的位移传感器测量压痕过程的载荷和位移。M.Nilsson[18]利用Hopkinson 装置中采集的入射、反射和透射信号来推导压头承受的载荷和位移信息,但是由于没有采纳任何二次加载的抑制技术,使得在数据处理中要采用复杂的两应变片法和迭代算法,造成数据处理的复杂性。
本文中,设计了用于动态压痕实验的SHPB 系统,采用S.Nemat-Nasser 的MT(momentum trap)[19]装置消除二次加载,利用入射杆和透射杆上应变片处测得的信号来计算压痕载荷和位移,对压痕全过程进行数值模拟,并对该装置的可行性进行分析和验证。利用该装置对无氧铜、钛、铝合金3 种不同材料进行动态压痕实验,得到一系列的材料动态性能。结果表明,本文中发展的动态压痕实验技术,具有测量精确可靠、应用简单方便等优点。
1 实验技术和方法
1.1 试样材料及几何尺寸
实验中测试的材料为LY12 铝合金、纯钛和无氧铜3 种材料。每个试样的尺寸为Ø12.7 mm×7 mm,粘连在透射杆的端面上。实验前对所有试样进行退火处理,并进行端面抛光。
1.2 实验装置简介
采用改进后的分离式Hopkinson 压杆(split Hopkinson pressure bar,SHPB)系统对试样进行动态实验研究,类似于静态压痕实验仪器。为了得到材料的动态硬度,在SHPB 系统的基础上,增加了动态压痕设备部分,包括硬质合金压头、套筒和试样3 部分。在动态压痕实验中,需要得到实验过后试样表面压痕的尺寸,为避免实验过程中的二次加载问题,增加了能量块装置[18]。SHPB 系统的入射杆、透射杆和子弹直径均为12.7 mm,材料为高强度合金钢,其中入射杆长1.2 m,透射杆长1 m,在不同冲击速度下,为了使压痕大小尺寸差别不大,选用了不同长度的子弹。实验中需获得试样的压痕深度及试样所受到的冲击载荷,压深和载荷都可以通过应变片上测得的信号推算出来
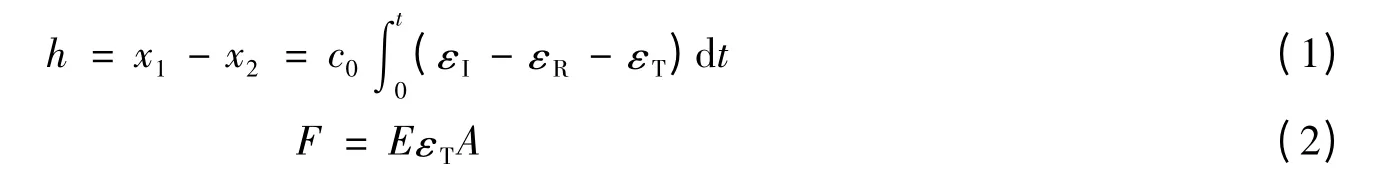
式中:h 是压痕的深度,x1、x2是试样两个端面的位移,c0是应力波在杆中的传播速度,εI、εR、εT分别是应变片捕捉到的入射信号、反射信号和透射信号,F 是试样在实验过程中所受的冲击载荷,E 是杆材料的弹性模量,A 是杆的端面面积。
1.3 压头参数的确定
通过有限元软件的模拟,得到冲击实验过程中压头所受到的最大应力,根据该应力,选择满足最大应力要求的YG6X 硬质合金[20]作为压头和压头支撑物的材料。为了保证波形能够在压头与钛合金套筒组合体中无损的传播,保护脆性的硬质合金,根据波阻抗匹配公式:ρ1c1A1+ρ2c2A2=ρ cA,计算钛合金套筒和硬质合金支撑物端面面积,实现硬质合金压头和钛合金套筒组合体与入射杆波阻抗的匹配,如图1 所示。采用2 种压头组合体:圆锥压头组合体和棱锥压头组合体,钛合金筒的外径为12.7 mm。圆锥压头锥角为110°,棱锥压头锥角为136°。
压头组合体与入射杆用502 胶粘连为一体,为了保证在实验过程中反射波无损地达到贴在入射杆上的应变片,同时也保证压头组合体牢固地固定在入射杆端面上,选择长30 mm 的压头支撑物和钛合金套筒。通过数值计算,得到30 mm 压头支撑物长度下压痕深度实验误差约4%。
1.4 实验的可行性验证
为确定实验中应变片测量信号计算的实验数据能够准确代表实验中试样的真实情况,通过ABAQUS 有限元软件对整个实验过程进行模拟。对比发现,通过分离式Hopkinson 压杆系统获得的压痕试样受到的冲击载荷与实验中的真实数据基本吻合,如图2 所示,从而得出了实验可行的结论。
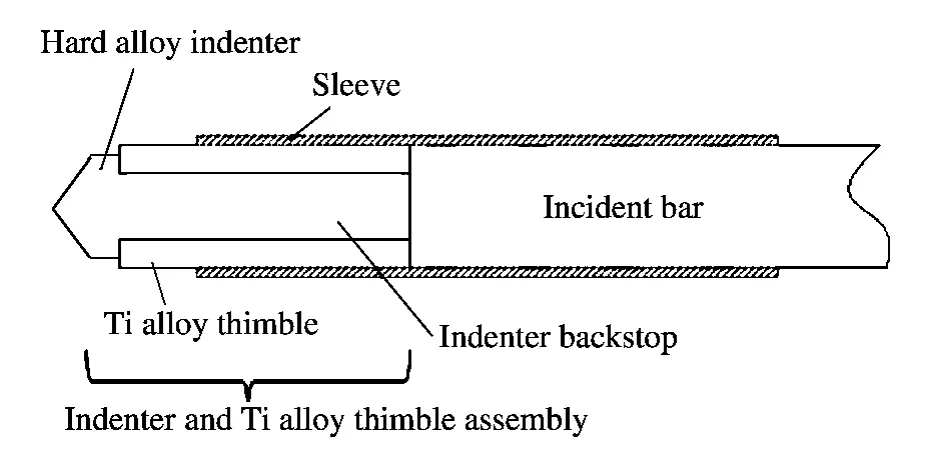
图1 压头与入射杆连接剖面图Fig.1 The cutaway view of the indenter and incident bar
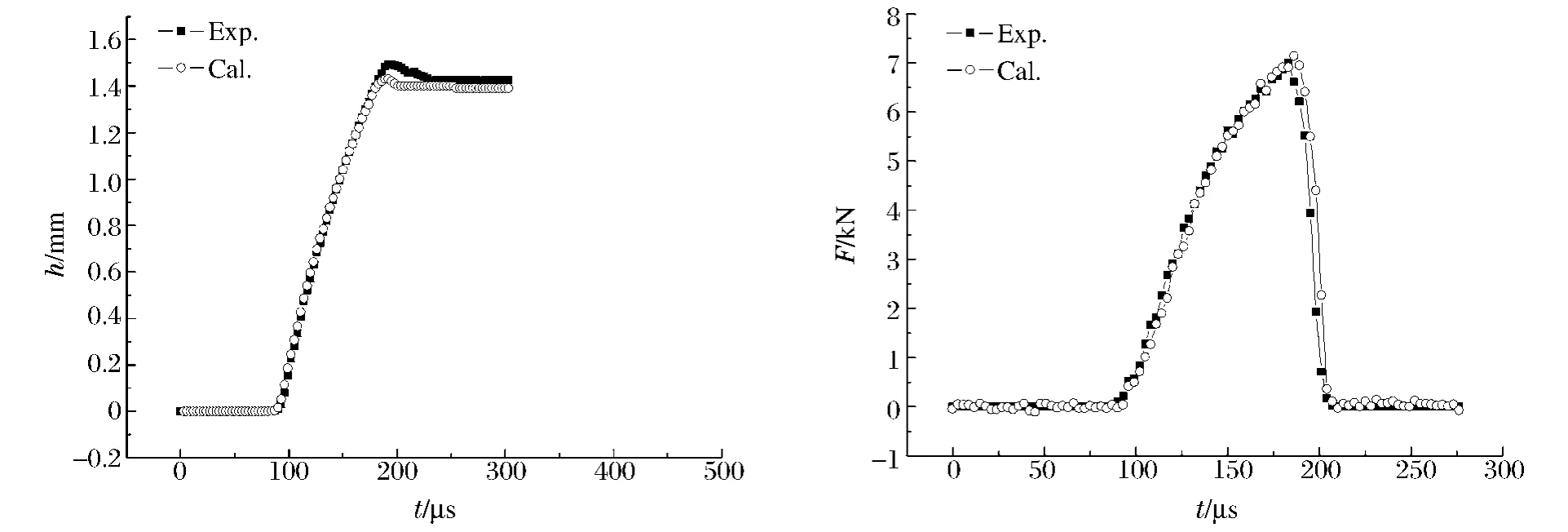
图2 压痕深度与冲击力的实验和计算结果对比Fig.2 The contrast of indentation and impact between experiment and calculation
2 实验结果
2.1 压痕的产生
在动态压痕冲击实验中选用126、266、395 mm 等3 种不同长度的子弹,得到一系列实验数据。图3是铝试样在实验后与数值模拟计算后的形状图。
压痕尺寸定义为试样的压痕面积,这样圆锥形和棱锥形压头下的压痕面积分别为
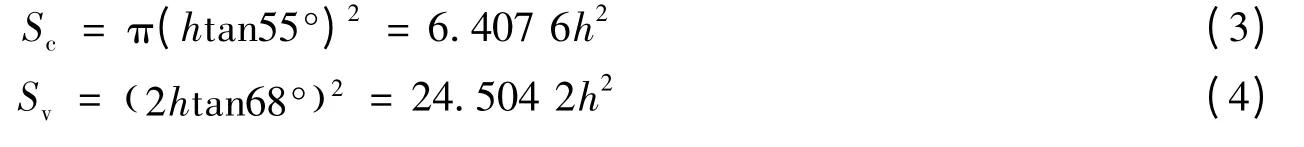
式中:h 是压痕深度。

图3 实验与有限元模拟下的铝合金试样分别在圆锥和Vickers 压头冲击后的形状Fig.3 Shapes of the aluminium sample under impact of cone and Vickers indenters in the experiment and numerical simulation
分析冲击实验过程中压痕的响应,如图4 所示,可以清楚地看出,随着时间增加到载荷峰值时刻,压痕的深度开始衰减。当冲击力载荷达到最大值时,压痕深度也达到最大值,压头组合体的速度为零。最后,压头组合体回弹,并获得一个离开速度。因此,动态压痕实验中,试样压痕的产生分为明显的3 个阶段:开始阶段、压痕阶段和回弹阶段。由图4 可以看出,压痕深度的产生与冲击力的产生对应于时间轴上起始点是基本一致的,因此可以说明2 个量之间的同步性。
2.2 实验结果误差分析
对试样的真实压痕尺寸与应变片信号计算得到压痕尺寸进行比较

式中:η 为误差,Le为实测得到的压痕对角线长度,Lc为应变片信号计算得到的压痕对角线长度。
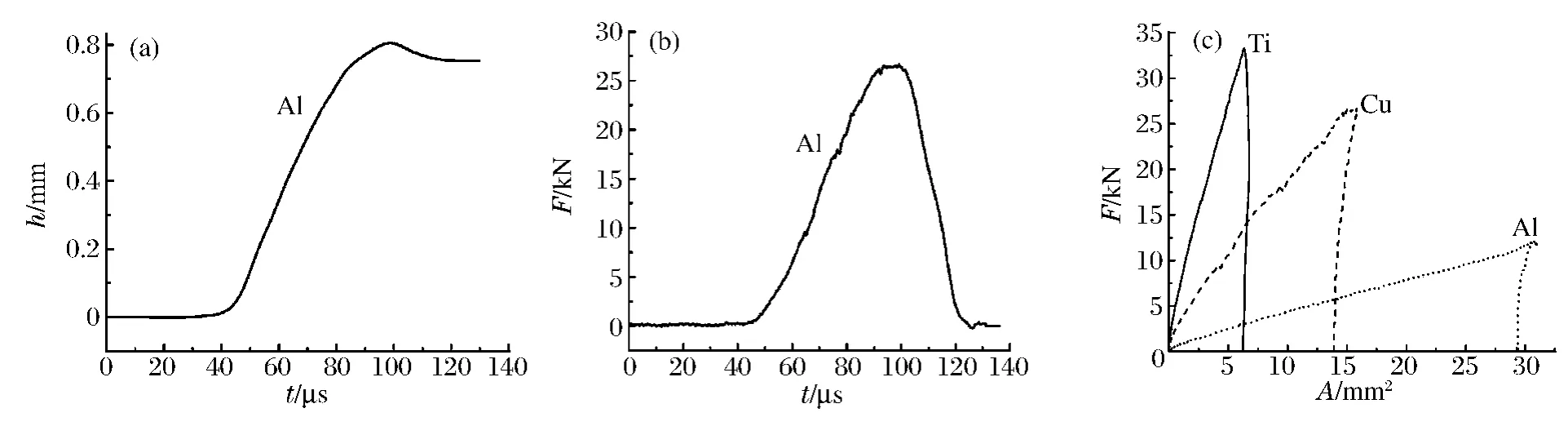
图4 铝试样压痕深度、冲击载荷与时间关系及3 种材料试样压痕面积与所受冲击载荷关系曲线Fig.4 Indentation-time and impact-time curves of the aluminiun sample and indentation acreage-impact curves of three kinds of samples

表1 3 种不同材料的部分试样计算压痕尺寸与实际压痕尺寸Table 1 Calculated and actual indentation sizes of partial samples of three kinds of different materials in experiment
对表1 中数据进行分析,由1.3 节可知,用应变片信号计算得到的压痕尺寸略小于实验中真实的压痕尺寸,产生偏差的主要原因是压痕尺寸的测量、反射波形的少量损失以及试样的弹性应变等造成的。
2.3 动态硬度
动态硬度的定义与静态硬度的定义类似,定义为试样所受载荷与压痕面积的比值。定义Vickers 压头下的动态硬度[17]为

同样,对于圆锥压头下的动态硬度[17]定义为
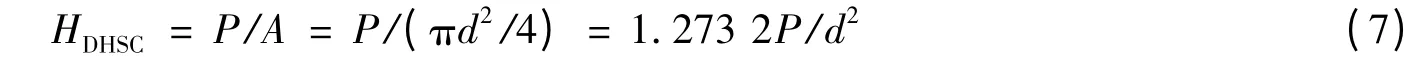
式中:P 是实验过程中试样所受到的冲击载荷的峰值,对于Vickers 压头,d 表示实验后压痕对角线长度的平均值,对于圆锥压头,d 表示实验后压痕直径长度的平均值。
表2 中给出了不同材料的试样在不同冲击速度下的动态硬度值。
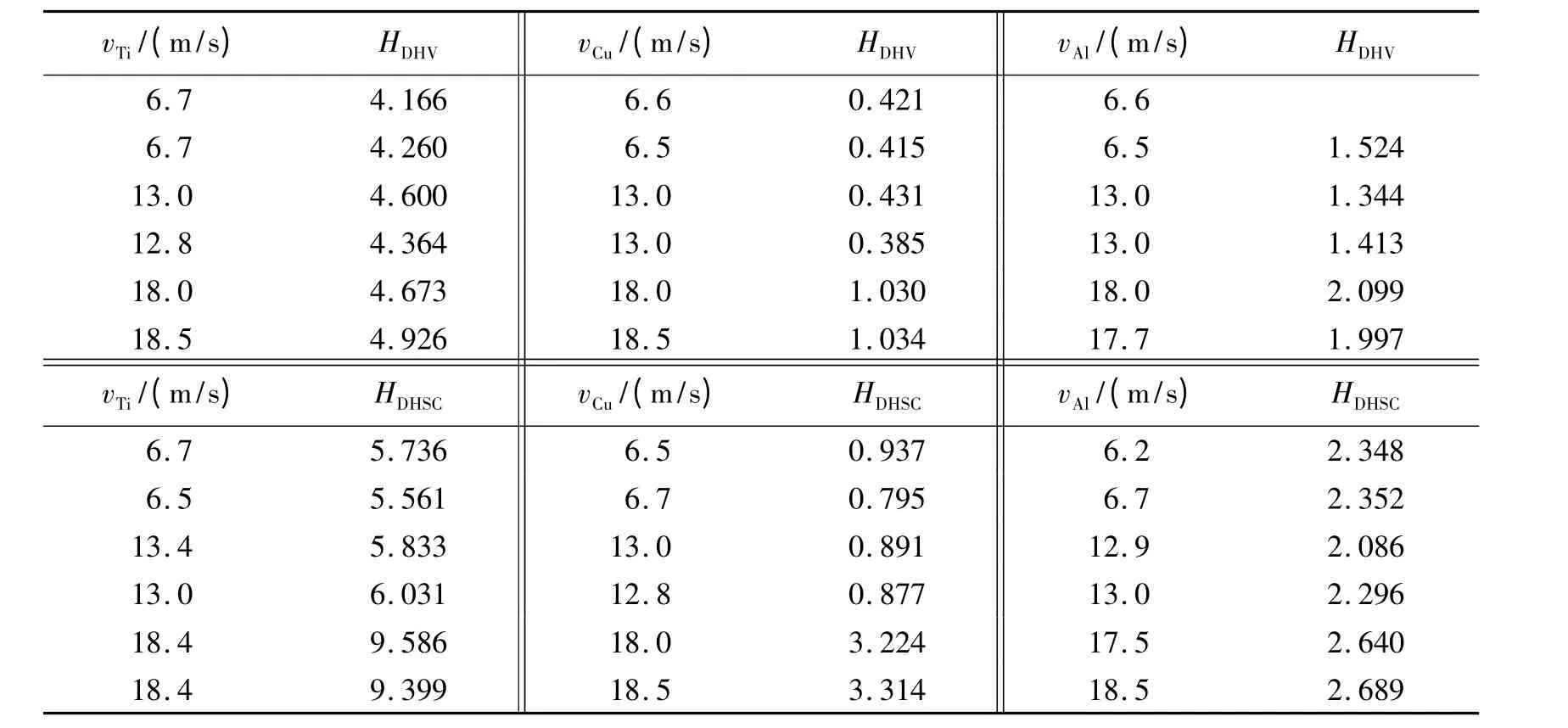
表2 3 种材料试样在不同冲击速度下的DHV 硬度和DHSC 硬度Table 2 DHV and DHSC hardness of samples of three kinds of material under different impact velocities
为了与动态硬度值相比较,在微硬度计上对3 种材料试样进行了准静态微硬度的测量。可以得到3 种材料的维氏硬度分别为:Ti,3.098;Cu,0.408;Al,1.312,与动态硬度相对比可以发现,材料的静态硬度是一个常数,动态硬度则随冲击速度的增加而增大。
2.4 材料的率敏感性
众所周知,钛和无氧铜在高应变率下表现出明显的率敏感性。当应变率达到103s-1量级时,它的流动应力对应变率的依赖性变得格外显著。为了通过动态压痕实验来研究材料的率敏感性,需要对平均应变率进行定义。
在压痕实验中,压痕区域变形极不均匀,应变在压痕顶点处最大,沿外围逐渐减小,在距离压头一定位置处减小为零;在整个压痕过程中,应变随时间变化的规律也非常复杂。因此,压痕区域的应变率不仅在空间分布上各点取值不同,在每一点处的应变率也是时间的函数。
通过有限元计算,得到基于经验的应变率确定方法。对于棱锥形压头,通过有限元软件模拟了不同子弹在不同冲击速度下的实验过程,取冲击后试样压痕紧靠尖端单元网格的方形环处各个点应变的平均值,将该应变曲线初始阶段的应变率定义为平均应变率。分别将这些平均应变率与相对应子弹的入射速度做对比,两者之间存在如下关系

G.Subhash 等[16]定义平均应变率为压痕的速度与压痕的尺寸的比值,他们将压痕形成的后期速度的平均值作为压痕的速度(如图4 所示),将压痕的尺寸定义为压痕的深度或对角线长度,很显然,这也是一个平均应变率的估算公式。在处理实验数据时,每次都需要找出压痕后期呈线性的部分,计算出压痕速度,这样较为繁琐。文中提出的公式,虽然在公式的获取上需要进行大量的有限元计算,但给出公式之后,应变率的确定就变得十分简便,在工程上具有更方便的应用。在相同的实验条件下,将文献[16]中定义的平均应变率与本文中定义的平均应变率进行比较,可以发现平均应变率的对数之间的误差不超过5%,从一个侧面也反映了公式(8)的可行性。
有了平均应变率之后,结合2.4 节得到的动态硬度,定义材料的率敏感性

式中:HD是材料的动态硬度,是试样的平均应变率。
将实验得到的DHV 硬度、DHSC 硬度及其他学者对3 种材料进行力学性能测试得到的流动应力进行量纲一处理,以静态的硬度以及低应变率下的流动应力为基准,将这种量纲一化后的硬度和流动应力记为N,3 种材料在不同应变率下的N 值如图5 所示。
从图5 可以明显地看出,不论是Vickers 压头还是圆锥压头下钛试样和无氧铜试样的DHV 和HSC动态硬度斜率随着试样所受到的应变率的增大而增加,由公式(9)可知,率敏感性也随着应变率的增加而不断增大。但对于铝合金试样而言,DHV 和DHSC 动态硬度随着应变率的变化而发生的变化要平缓得多,相应的率敏感性就要小,率敏感性的变化也小。因此可知无氧铜和钛材料的率敏感性高于铝合金材料的率敏感性。这与实际工程中3 种材料的率敏感性关系一致。
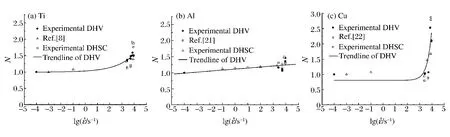
图5 钛、铝、无氧铜的应变率与不同间的N 值间的关系Fig.5 Relation between strain rate and N of Ti,Al and Cu samples
3 结 论
介绍了一种新的确定材料动态压痕硬度的实验技术,并将这种技术发展用来测试工程材料的率敏感性。将该种方法获得的材料的动态硬度值与广泛应用的硬度计下测得的硬度值进行比较,发现所测材料的动态硬度值略大于静态硬度值。通过对不同应变率下的动态压痕实验结果分析表明,本文中用到的3 种材料的动态硬度均表现出不同的应变率敏感性,与实际工程中的敏感性具有很好的一致性。
[1] Almasri A H,Voyiadjis G Z.Effect of strain rate on the dynamic hardness in metals[J].Journal of Engineering Materials and Technology,2007,129(4):505-512.
[2] Tabor D.The hardness of metals[M].London:Oxford University Press,1951:44-93.
[3] Dugdale D S.Cone indentation experiments[J].Journal of the Mechanics and Physics of Solids,1954,2(4):265-277.
[4] Oliver W C,Pharr G M.An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments[J].Journal of Materials Research,1992,7(6):1564-1583.
[5] Clifton R J.Dynamic plasticity[J].Journal of Applied Mechanics of the ASME,1983,50(4b):941-952.
[6] Meyers M A.Dynamic behavior of materials[M].New York:Wiley,1994:488-563.
[7] Subhash G.The Constitutive behavior of refractory metals as a function of strain rate[J].Journal of the Minerals Metals&Materials Society,1995,47(55):55-58.
[8] Nemat-Nasser S,Guo W G,Cheng J Y.Mechanical properties and deformation mechanisms of a commercially pure titanium[J].Acta Materialia,1999,47(13):3705-3720.
[9] Tabor D.A simple theory of static and dynamic hardness[J].Proceedings the Royal of Society:A,1948,192(1029):247-274.
[10] Marshall D B,Evans A G,Nisenholz Z.Measurement of dynamic hardness by controlled sharp-projectile impact[J].Journal of American Ceramic Society,1983,66(8):580-585.
[11] Sundararajan G,Shewmon P G.The use of dynamic impact experiments in the determination of the strain rate sensitivity of metals and alloys[J].Acta Metallurgica,1983,31(1):101-109.
[12] Tirupataiah Y,Sundararajan G.A dynamic indentation technique for the characterization of the high strain rate plastic flow behavior of ductile metals and alloys[J].Journal of the Mechanic and Physics of Solid,1991,39(2):243-271.
[13] Nobre J P,Gras A M.Resistance of a ductile steel surface to spherical normal impact indentation:Use of a pendulum machine[J].Wear,1997,211(2):226-236.
[14] Lu J,Suresh S,Ravichandran G.Dynamic indentation for determining the strain rate sensitivity of metals[J].Journal of the Mechanics and Physics of Solid,2003,51(11/12):1923-1938.
[15] Koeppel B J,Subhash G.Characteristics of residual plastic zone under static and dynamic Vickers indentations[J].Wear,1999,224(1):56-67.
[16] Subhash G,Koeppel B J,Chandra A.Dynamic indentation hardness and rate sensitivity in metals[J].Journal of Engineering Materials and Technology,1999,121(3):257-263.
[17] Anton R J,Subhash G.Dynamic Vickers indentation of brittle materials[J].Wear,2000,239(1):27-35.
[18] Nilsson M.Dynamic hardness testing using a split hopkinson pressure bar apparatus[R].Swedish Defence Research Agency,SE-147 25 Tumba.2002:35.
[19] Nemat-Nasser S,Isaacs J B,Starrett J E.Hopkinson techniques for dynamic recovery experiments[J].Proceedings the Royal of Society:A,1991,435(1894):371-391.
[20] 张丝雨,马维田,马雁冰,等.最新金属材料牌号、性能、用途及中外牌号对照速用速查实用手册[M].北京:中国科技文化出版社,2005:1654-1665.
[21] Nemat-Nasser S,Guo W G,Cheng J Y.High strain rate properties of selected aluminium alloys[J].Materials Science and Engineering,1999,278(1-2):225-235.
[22] Nemat-Nasser S,LI Yu-long.Flow stress of F.C.C.polycrystals with application to OFHC Cu[J].Acta Materialia,1998,46(2):565-577.
