光通量法在SHPSB 剪切应变测量中的应用*
2011-02-26赵鹏铎卢芳云李俊玲林玉亮谭多望
赵鹏铎,卢芳云,陈 荣,李俊玲,林玉亮,谭多望
(1.国防科学技术大学理学院,湖南 长沙410073;2.中国工程物理研究院流体物理研究所冲击波物理与爆轰物理国防科技重点实验室,四川 绵阳621900)
在各类涉及爆炸和冲击加载的领域中,材料的动态本构关系始终是重要的研究课题。动态本构关系涉及应力张量、应变张量,应变率以及温度等变量之间的关系。传统的一维波加载实验只能确定部分本构参数,动态压剪复合加载实验则可以为本构关系提供更加完整的实验参数。除此之外,材料的屈服、损伤演化、失效、相变等均与剪切密切相关。材料动态压-剪加载的研究不仅丰富了材料的动态力学现象,拓展了研究范围,而且对于认识材料动态响应的演化规律和机理有重要的意义[1]。
卢芳云等[2]提出了分离式霍普金森压剪杆实验的思想,主要借鉴了传统的SHPB 与动态压剪复合平板冲击加载实验技术[3-6],对传统SHPB 进行了拓展:入射杆端头为楔形状,同时使用了2 个透射杆。并讨论了相对于已有的动态压剪复合加载实验[7-10]的优点。
L.J.Griffiths 等[11]采用光通量法对碳纤维复合材料的动态性能进行了研究。唐志平等[12]对光通量法用于动态力学量测试的可行性进行了系统分析和研究,并与传统的电阻应变片法作了比较。结果表明:光通量法法能可靠地用于准静态直至应变率达105s-1范围内质点位移、速度,以及试件应变、应变率、应力和泊松比等力学量的测量。K.T.Ramesh 等[13]利用光通量法测量了SHPB 实验中试样的横向变形。李玉龙等[14]改进了Ramesh 测试装置,在激光器前加设了光学准直部件,使激光光束成为平行光,并测试了动态拉伸试件的径向应变。
本文中利用半导体准直激光器,采用光通量法,对SHPSB(split Hopkinson pressure bar)实验技术中试样的剪切应变测量进行实验研究,并对测试系统进行不确定度评定。最后对某含铝PBX 试样的剪切应变测试值和文献[2]给出的理论计算结果进行对比分析。
1 实 验
1.1 装置及基本原理
实验光学测试系统主要包括:半导体准直激光器、光学狭缝、光电接收器以及光学挡板,如图1 所示。其中准直激光器输出功率为20 mW,用以输出波长为660 nm 的平行激光。激光光束与透射杆平行,激光光斑为圆形,经过光学狭缝,光斑变为均匀带状。光电接受器主要包括接受透镜和光电传感器。接收透镜将激光汇聚到光电传感器的感光面,这样光电传感器的输出电压就与激光的通光量成正比。光电传感器的响应频率为2 MHz,系统噪音小于0.4 mV。光学挡板1 和光学挡板2 通过铝箍,分别与入射杆和透射杆固定连接。由于光学挡板1 和光学挡板2 的遮挡,投射在光电接收器上的光斑呈矩形。实验中,试样分别与入射杆、透射杆固连,试样界面的切向运动与实验杆界面的切向运动是一致的,而光学挡板1 与入射杆固定连接,因此入射杆界面的切向运动和挡板1 的切向运动是一致的。同理,光学挡板2 与透射杆界面的切向运动一致。当试样受载剪切变形时,光学挡板1 与光学挡板2 出现切向的相对运动,于是造成光通量的变化,而与光电接收器连接的示波器记录了由光通量变化对应的电压变化值。如果试样仅沿着透射杆轴向运动,光通量将不会改变,即无变化电压输出。
实验采用精密测微丝杆对实验测试系统进行标定。即利用精密测微丝杆在垂直于光路的方向,遮挡激光光斑来记录光斑宽度变化量以及输出电压值。测微丝杆的变化范围是0 ~10 mm,变化间隔为0.1 mm。丝杆的运动造成矩形光斑宽度S 的变化,即光斑宽度的变化(ΔS)就对应着光电传感器的输出电压变化(ΔU)。图2 给出了两次标定实验结果,在两次标定实验中测微丝杆的位置相距4 cm。由于激光光束为光强均匀的平行光,两次标定结果基本一致,且ΔS 与ΔU 高度线性相关


图1 实验装置示意图Fig.1 Schematics of the experiment
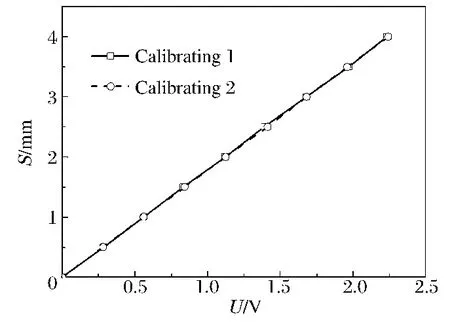
图2 实验标定结果Fig.2 Results of the calibration
由此标定出相对于单位电压变化所对应的距离变化值,即电压-距离转换系数k(mm/V)。假设试样的原始厚度为l0,而光束变化值与试样两个界面的相对切向位移一致,则试样剪切应变为

剪切应变率可以由相对位移的导数,即相对速度Δv 表示

剪切应变测量系统的不确定度主要来源是:电压-距离转换系数k 标定过程引入的不确定度,光电接收器的系统噪声引入的不确定度。由图2 计算出k 引入的标准不确定度[15]u1=0.003 14 mm/V。光电接收器的最大噪声为0.4 mV,以均匀分布考虑[15],则由均匀分布的标准不确定度计算方法可知,由光电接收器的系统噪声引入的标准不确定度,而合成标准不确定度可以表示为
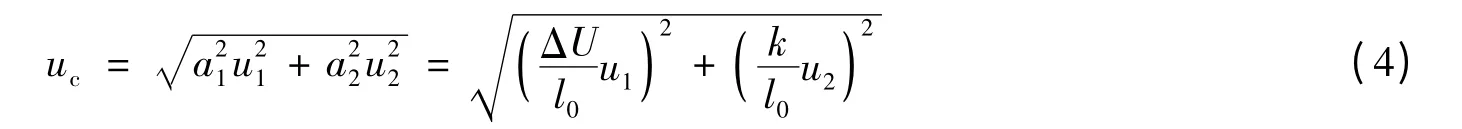
式中:ai是第i 项不确定度的灵敏度系数,其数值等于对公式(2)关于k 与ΔU 分别求偏导数。例如某次实验中,试样的厚度是5 mm,实验采集到的峰值电压ΔU=500 mV,则测试的剪切应变的标准不确定度uc=0.03%,这对于剪切破坏应变较小的脆性材料(γc<5%)来说,测量结果的不确定度依旧是小量,这表明本文提出的剪切应变测试方法具有较高的可靠性。
1.2 性能验证实验
剪切应变测试方法是否有效,关键是:(1)所选择的准直激光器的光斑在不同位置是否均匀;(2)激光接收器响应是否满足动态实验要求;(3)挡板与实验杆连接是否完全固连。
问题(1)已经由静态标定实验结果回答,如图2 所示。为了解决其余问题,设计如图3 所示的子弹撞击长杆验证实验。在实验杆端使用铝箍将光学挡板与杆固连,利用准直激光器与光电接收器对实验杆端面的运动时程曲线进行记录。实验杆上应变片记录了入射与反射应变,利用一维应力波理论计算实验杆端面的位移时程曲线。图4 给出了2 种方法所测得的杆端的位移时程曲线,其中实线是通过应变片计算的杆端位移时程曲线,虚线为激光系统测试的结果,图中曲线第2 次上升是由于应力波反射产生二次加载造成的位移。
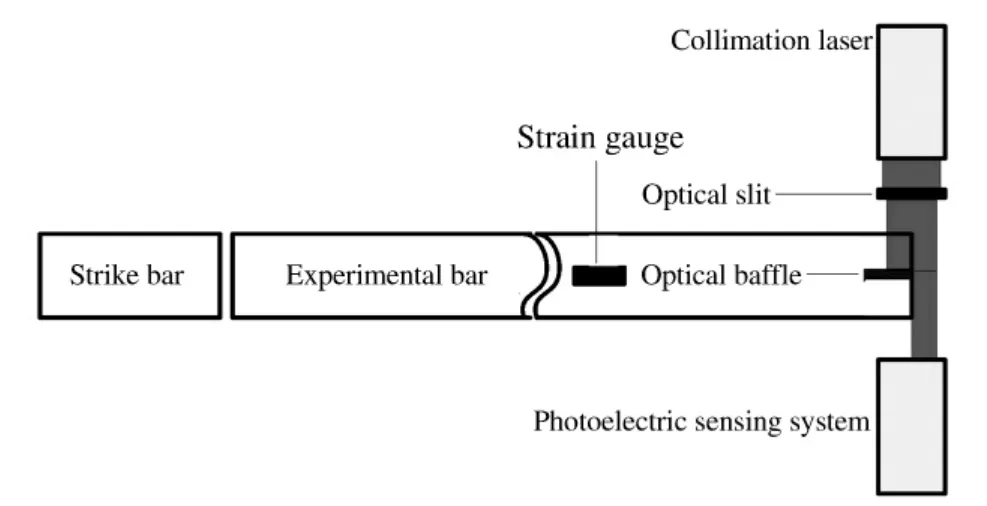
图3 实验装置示意图Fig.3 Schematics of the valid experiment
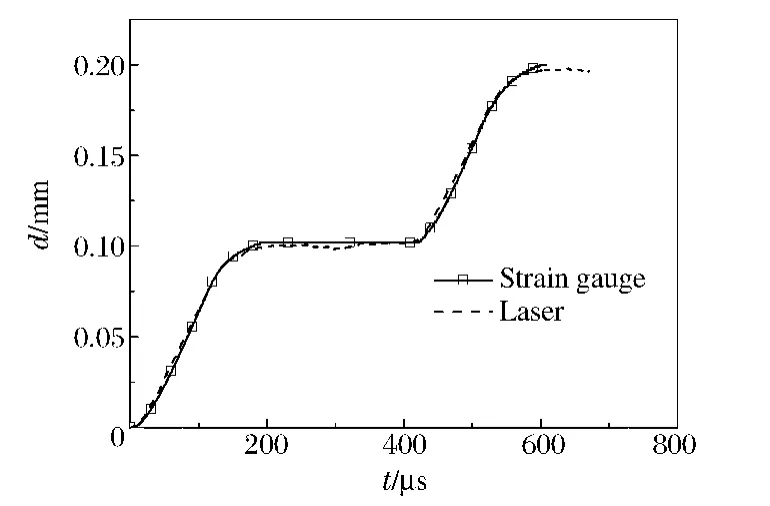
图4 杆端的位移时程曲线Fig.4 Displacement history of the end of the bar
由图4 可知2 种方法所得的位移时程曲线一致,上升斜率相同。这表明接收器的频响满足动态实验需要;挡板与实验杆固连,未出现松动,表明挡板与实验杆连接方法有效。问题(2)、(3)得到解决,因此本文中提出的剪切应变测试技术是有效的。
2 实验结果与讨论
对密度为1.7 g/cm3的含铝PBX 炸药进行SHPSB 实验。实验采用立方体试样,其尺寸为13 mm×13 mm×5 mm。图5 给出了典型的剪切应力、应变的原始波形,其中剪切应力测试方法与文献[2]相同。由图5 可知剪切应力与剪切应变测试的原始信号的起跳时间相当,前者的峰值时刻早于后者。图6 是典型的剪切应力、应变时程曲线,由图6 可知,2 种方法获得的剪切应变时程曲线不一致。
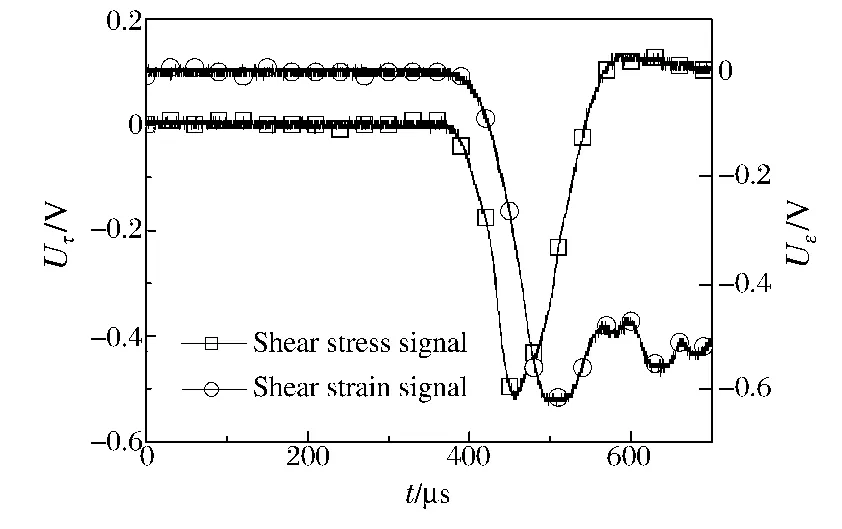
图5 典型的实验原始波形Fig.5 Oscilloscope signals of test
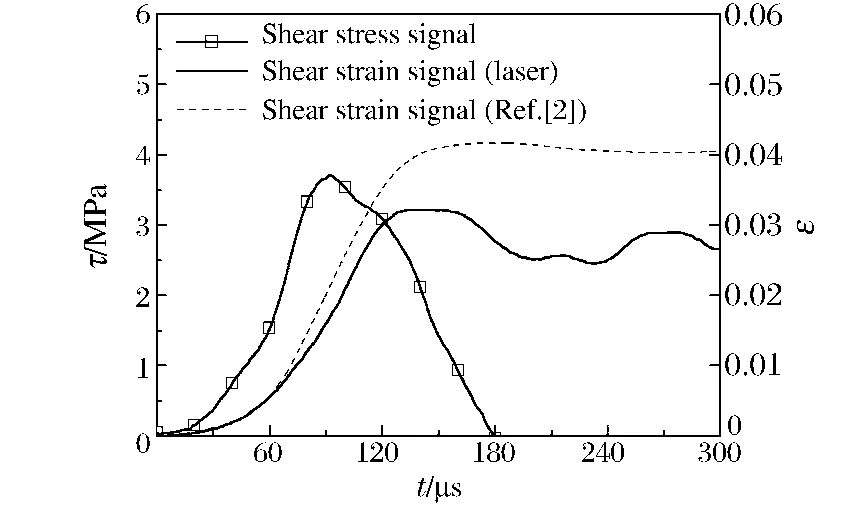
图6 典型的剪切应力、应变时程曲线Fig.6 Shear stress and strain histories of the specimen
文献[2]给出的剪切应变率为
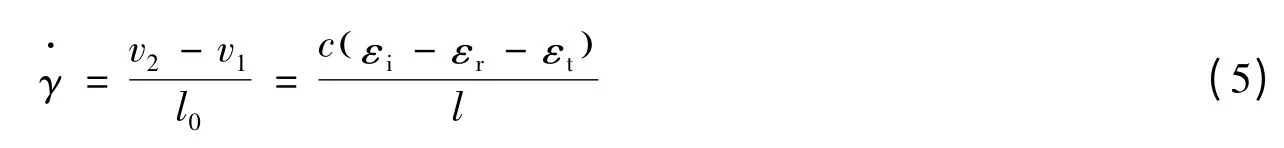
式中:l0为试样的厚度,v1、v2分别为试样两端的切向质点速度,εi、εr、εt分别为入射波、反射波和透射波产生的剪切应变为剪切波速,G、ρ0分别为透射杆的剪切模量与密度。文献[2]中是将一维弹性剪切应力波中应变与横向速度的关系近似表示为透射剪切应变与切向质点速度的关系,即

在压剪复合平板冲击实验中满足公式(6),即没有考虑侧向边界对剪切波的影响。在长杆中,加载脉宽大于杆的直径,侧向边界对剪切波传播始终是有影响的。这类扰动被定义为弯曲波[16]。弯曲波的动力学方程不但要考虑动量守恒,同时要考虑动量矩守恒,因此公式(6)已不完全适用。图7 中曲线1是利用LS-DYNA 模拟的弯曲波在细长杆中传播的横向速度曲线,代表了杆上某一横截面积内单元的平均横向速度,曲线2 代表了该截面内单元平均剪切应变与剪切波速乘积结果,即公式(6)的右侧项。
由图7 可知,利用公式(6)计算的杆的横向速度相对实际横向速度明显偏小。在SHPSB 透射杆上利用公式(6)建立横向速度与剪切应变的关系是不准确的,透射杆与试样端面的实际横向速度大于文献[2]计算结果。而试样的剪切应变可表示为
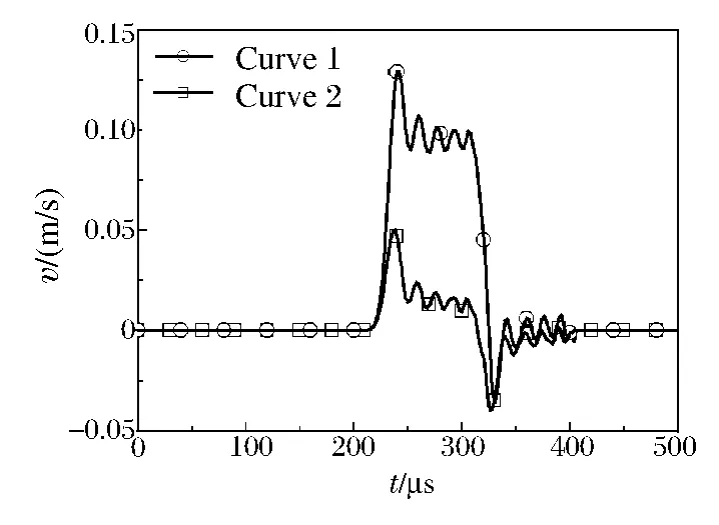
图7 横截面的横向速度时程曲线Fig.7 Transverse velocity histories of the bar
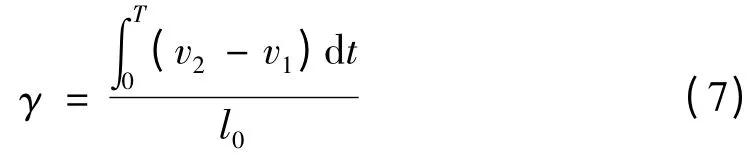
式中:T 是加载波宽。透射杆的实际横向速度v1>c εt,则
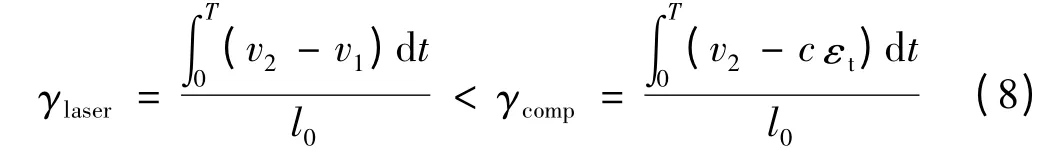
公式(8)基于光通量法测量的剪切应变值小于文献[2]处理结果。由于在初始上升阶段(图7 中两曲线的上升沿部分),透射杆-试样截面的横向速度明显小于入射杆-试样截面的横向速度,即v1<v2,并且在此阶段,v1与c εt相差较小,所以曲线上升阶段γlaser与γcomp基本吻合,如图6 所示。随着v1与c εt的差值以及v1增大,γcomp曲线逐渐高于γlaser时程曲线。剪切应变测试信号在达到峰值平台之后,信号出现了上下波动,如图5 所示。这可能是由于试样/实验杆界面连接出现了破坏,使得试样界面的运动与实验杆端面运动不再一致,此时波动的信号已经不能反映试样的剪切变形。信号出现波动的时刻对应于实验加载末段,剪切应力已降低到1 MPa 左右,如图6 所示,此阶段已不是实验关注的主要阶段。
3 结 论
利用光通量法对SHPSB 实验中的剪切应变进行了实验测量,得到了试样的剪切应变与剪切应变率。光学测试系统的标定结果和性能测试实验结果表明利用文中提出的基于光通量法的剪切应变测量技术能够准确地测量SHPSB 试样的剪切应变。测量系统的不确定度分析结果表明该测量方法具有较高的可靠性。对比分析了基于光通量法测量的剪切应变结果与理论近似处理结果,表明光通量法测量的剪切应变相较应用一维剪切波理论处理的剪切应变值更加准确。
[1] 唐志平.压剪复合平板冲击加载技术进展及其应用[J].力学进展,2007,37(3):398-408.TANG Zhi-ping.Progress and application of combined compression and shear wave loading technique[J].Advances in mechanics,2007,37(3):398-408.
[2] 崔云霄,卢芳云,林玉亮,等.一种新的高应变率复合压剪实验技术[J].实验力学,2006,21(5):584-590.CUI Yun-xiao,LU Fang-yun,LIN Yu-liang,et al.A new combined compression-shear loading technique at high strain rates[J].Journal of Experimental Mechanics,2006,21(5):584-590.
[3] Tong W.Pressure-shear stress wave analysis in plate impact experiments[J].International Journal of Impact Engineering,1997,19(2):147-164.
[4] Clifton R J,Klopp R W.Pressure-shear plate impact testing[Z].American Society for Metals,1985:230-239.
[5] Abou-Sayed A S,Clifton R J.Pressure-shear impact of 6061-T6 aluminum due to oblique-plate-impact[J].Journal of Applied Mechanics,1977,44(1):85-88.
[6] Gilat A,Clifton R J.Pressure-shear waves in 6061-T6 aluminum and alpha-tianium[J].Journal of the Mechanics and Physics of Solids,1985,33(3):263-284.
[7] Huang H,Feng R.A study of the dynamic tribological response of closed fracture surface pairs by Kolsky-bar compression-shear experiment[J].International Journal of Solids and Structures,2004,41(11/12):2821-2835.
[8] Meyer L W,Krüger L.Shear testing with hat-shaped specimen,metals handbook:Mechanical testing and evaluation[Z].American Society for Metals,2000:994-1000.
[9] Rittel D,Ravichandran G,Venkert A.The mechanical response of pure iron at high strain rates under dominant shear[J].Materials Science and Engineering:A,2006,432(1/2):191-201.
[10] Rittel D,Lee S,Ravichandran G.A shear-compression specimen for large strain testing[J].Experimental Mechanics,2002,42(1):58-64.
[11] Griffiths L J,Martin D J.Study of dynamic behavior of a carbon-fiber composite using split Hopkinson pressure bar[J].Journal of Physics,D:Applied Physics,1974,7(17):2329-2344.
[12] 唐志平,胡时胜,王礼立.动态力学量的光电测试法[J].实验力学,1991,6(4):401-406.TANG Zhi-ping,HU Shi-sheng,WANG Li-li.Photoelectric method for measuring dynamic mechanical variables[J].Journal of experimental mechanics,1991,6(4):401-406.
[13] Ramesh K T,Narasimhan S.Finite deformations and the dynamic measurement of radial strains in compression Kolsky bar experiments[J].International Journal of Solids and Structures,1996,33(25):3723-3738.
[14] Li Y,Ramesh K T.An optical technique for measurement of material properties in the tension Kolsky bar[J].International Journal of Impact Engineering,2007,34(4):784-798.
[15] 沙定国.误差分析与测量不确定度评定[M].北京:中国计量出版社,2003.
[16] Meyers M A.Dynamic behavior of materials[M].New York:John Wiley&Sons,Inc,1994.
