一种新型SPH-FEM 耦合算法及其在冲击动力学问题中的应用*

张志春，强洪夫，高巍然

(第二炮兵工程学院，陕西 西安710025)

SPH 最早由L.B.Lucy［1］、R.A.Gingold 等［2］用于解决三维开放空间天体物理学问题，特别是多变性问题。SPH 的近似函数建立在一系列离散的粒子上，不需要借助网格，通过使用一系列任意分布的粒子来求解相应的偏微分方程组，从而得到精确稳定的数值解。由于不需要借助网格，并且具有Lagrange性质，SPH 方法在处理大变形、自由表面等问题时具有明显的优势，目前已经广泛应用于连续固体力学和流体力学。但是在固体力学领域，SPH 的计算精度和效率较有限元方法低，并且其核函数不具有Kronecher delta 张量的性质，施加边界条件困难。因此耦合SPH 和FEM，在大变形区域使用SPH 粒子离散，小变形区域使用有限元离散，是计算冲击动力学问题的一种有效手段。

在同一材料中同时使用SPH 和FEM，耦合界面的计算是问题的关键。在这方面G.R.Johnson［3-4］和S.Ferna＇ndez-Me＇ndez 等［5］分别提出了各自的算法。G.R.Johnson 将SPH 粒子固结在有限元节点，通过固结的粒子传递与有限单元之间的相互作用力，但在计算界面粒子应变率时没有考虑邻近有限元节点的影响，无法保证耦合界面物理量的连续性。S.Ferna＇ndez-Me＇ndez 在有限单元和SPH 粒子之间设置了过渡区域，在过渡区域使用混合插值函数，不需要将有限元节点替换为粒子，但混合插值函数的计算过于复杂。

本文中，为解决SPH 和FEM 耦合界面的计算问题，提出一种新型耦合算法。将SPH 粒子固结在有限元节点，在有限元节点设置背景粒子，通过背景粒子的方式将有限元节点纳入SPH 粒子的邻近搜索列表。这种方法可避免SPH 的光滑核函数被边界截断，消除其边界效应，确保耦合界面处物理量的连续性。使用该耦合算法对圆柱形钢弹正冲击钢板进行三维数值模拟，其中钢弹和钢板中心区域采用SPH 离散，钢板其余区域采用有限元离散，施加固支边界条件;钢板参数的计算采用含损伤的Johnson-Cook 本构模型和Grüneisen 状态方程。子弹与靶板之间采用SPH 粒子接触算法。

1 SPH-FEM 耦合算法

1.1 算法流程

如图1 所示，SPH 粒子固结在有限元节点，其中小实线圆代表SPH 粒子，大虚线元代表粒子i 的支持域，小虚线元代表设置在有限元节点处的背景粒子。背景粒子具有SPH 粒子的属性，其质量、位置、速度、应力与相应有限元节点保持一致。计算流程如图2 所示，在每个时间步开始前，有限元节点的质量、位置、速度、应力传递给相应的背景粒子。在每个时间步结束后，界面处SPH 实粒子的位置、速度传递给相应的有限元节点。SPH 粒子采用跳蛙格式求解Navier-Stokes 方程，有限元采用中心差分法求解显示动力学方程。对SPH 粒子进行数值积分时，有限元节点以背景粒子的形式加入SPH 邻近搜索算法中，即任何位于邻近搜索范围内的SPH 粒子和有限元节点都被加入到临近列表。如对实粒子i 的积分包含SPH 粒子n1、n2、…、n5和有限元节点n6、n7、n8。背景粒子仅被动地被实SPH 粒子搜索，而自身不进行SPH 数值积分，数据的更新由相应的有限元节点确定。

使用该SPH-FEM 耦合算法处理耦合界面问题，对于SPH 部分，由于将耦合界面附近的有限元节点纳入到粒子的邻近搜索列表，积分时不会被界面截断，消除了SPH 的边界效应。对于有限元部分，界面处有限元节点数据由对应的SPH 粒子确定，相当于在耦合界面处对有限单元施加了边界条件，由于有限元形函数满足Kronecher delta 张量性质，该方案是可行的。

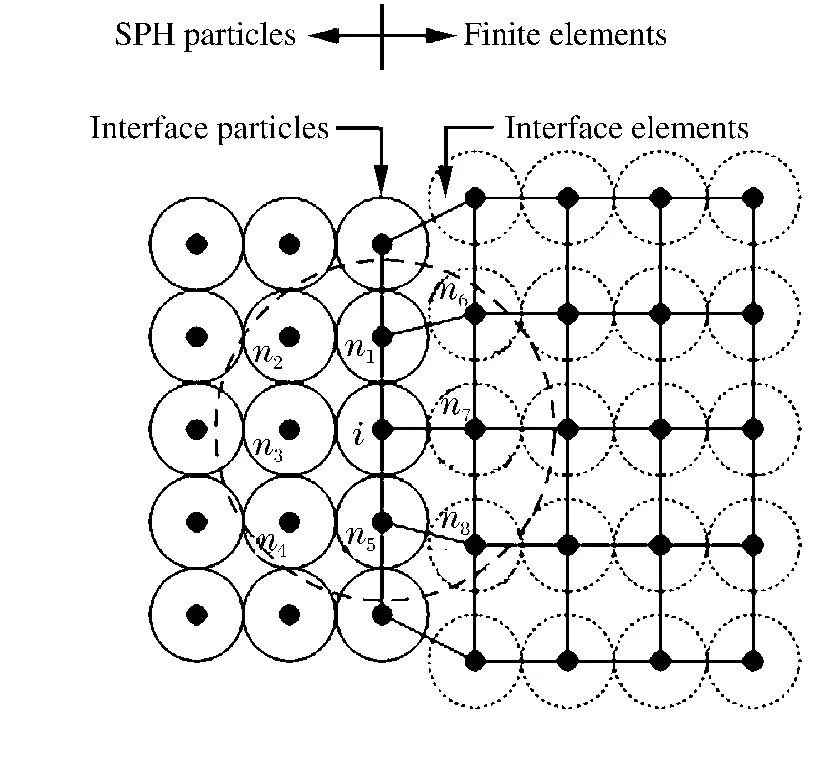
图1 SPH 粒子固结在有限单元Fig.1 SPH particles attached to finite elements

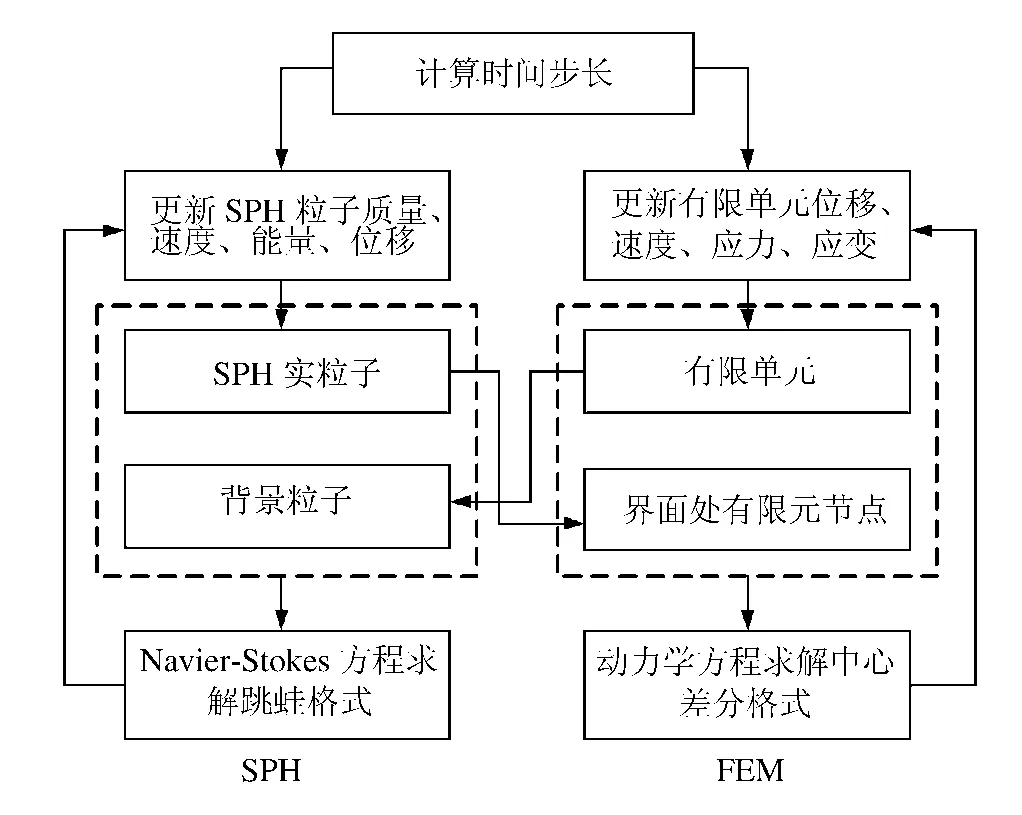
图2 SPH-FEM 耦合算法流程Fig.2 A solution procedure for the coupled SPH-FEM algorithm

1.2 时间步长控制

如图2 所示，SPH 部分采用跳蛙格式求解Navier-Stokes 方程，具体步骤如下:

(1)第1 个时间步结束后

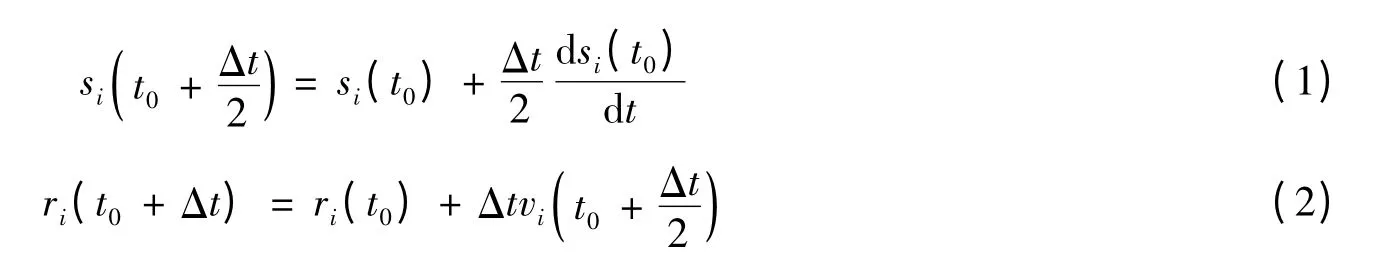
(2)在随后的每个时间步开始前

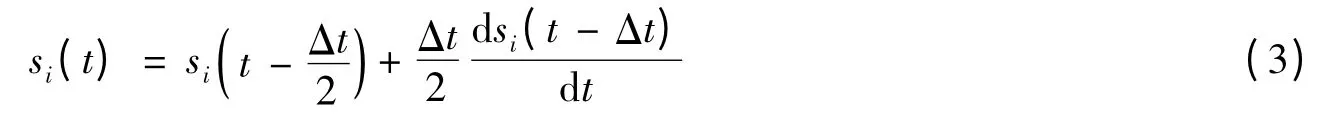
(3)在每个时间步结束后

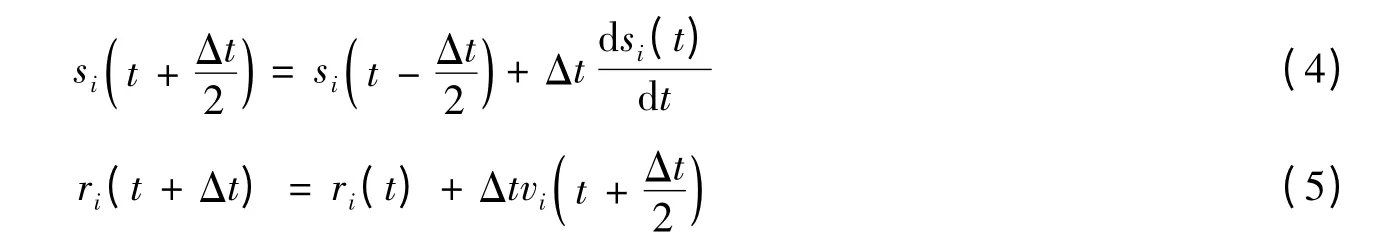
式中:si可以表示粒子i 的密度、速度和能量，ri和vi分别表示粒子i 的位置和速度，t 表示时间，Δt 表示时间步长。

对于有限元部分，采用中心差分法求解显示动力学方程，节点加速度、速度和位移分别为

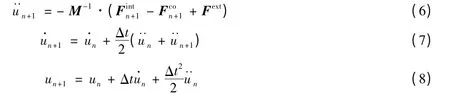
式中:M 是系统集中质量矩阵，Fint是内力，Fco是粘性力，Fext是外力。

在Lagrangian 框架下，SPH 与FEM 的耦合要求两者的积分必须同步，数据的传输必须是在同一时间点。这就要求在每一步计算中采用相同的时间步长，在此选择SPH 与FEM 时间步长的较小者

式中:SPH 时间步长ΔtSPH=βh/c，FEM 时间步长ΔtFEM≤L/c，其中h 是SPH 的光滑长度，L 是最小单元尺寸，c 是材料声速，β 是时间步长比例系数。

2 数值算例

为验证SPH-FEM 耦合算法的准确性，对杆一端受压和圆柱形钢弹正冲击钢板的问题进行了计算。采用J.J.Monaghan［6］提出的人工应力法来消除拉伸不稳定性造成的数值断裂，采用强洪夫等［7］提出的完全变光滑长度法来消除变光滑长度带来的影响。

2.1 杆一端受压

为验证SPH 粒子与有限单元耦合界面物理量的连续性，对方形杆一端受压问题进行计算。杆件的尺寸为5 mm×5 mm×100 mm，采用线弹性材料模型，密度ρ=7.83 t/m3，弹性模量E=207 GPa，泊松比ν=0.3。如图3 所示，杆件一半离散为1 835 个SPH粒子，另一半离散为1 250 个有限单元。在有限元一端突加矩形脉冲载荷，加载类型为均布压强p=40 GPa，加载时间为0 ～1 μs，计算总时间为14 μs。为了进行对比验证，相同的模型完全用有限元离散进行了计算。

图4 为耦合界面附近的SPH 粒子750、800、1 050、1 100 和有限元节点909、910、1 215、1 216 沿z 轴的速度和应力曲线，其中虚线表示对比算例中与SPH 粒子相同位置处节点的速度和应力。因为4 个粒子和4 个节点分别沿杆中心线对称分布，其速度和应力曲线分别重合，表明该算法完全满足对称性要求。初始时刻，速度和应力均为0，之后杆件产生沿z 轴的应力波，在t=10.5 μs 和t=11.0 μs，节点和粒子最大速度vz分别达到-582 和-539 m/s，应力最大值σz分别达到-27.3 和-27.9 GPa。图4 表明耦合界面两侧粒子的运动与节点保持一致，并且与对比算例中相同位置处的节点也保持一致，表明该耦合算法满足耦合界面处物理量的连续性要求。

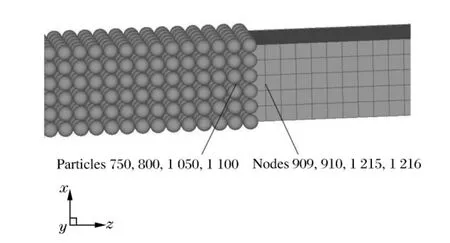
图3 杆一端受压模型Fig.3 The model of a bar pressed at one end

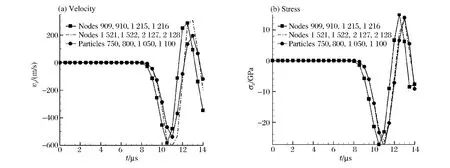
图4 耦合界面速度和应力曲线Fig.4 Plots for velocity and stress of the coupled interface

2.2 圆柱形钢弹正冲击钢板

对Arne tool 钢制圆柱弹丸与Weldox 460 E 钢板正冲击发生冲塞破坏的过程进行三维数值计算，计算模型如图5 所示。其中钢弹及靶板中心区域采用SPH 粒子离散，粒子间距1 mm，粒子总数47 133。靶板其余部分采用六面体单元离散，粒子附近网格尺寸为1 mm，其余部分网格尺寸由靶板中心向四周逐渐增大，单元总数18 816。子弹与靶板初始间距2 mm，靶板四周施加固支边界条件，计算时间160 μs。子弹与靶板的接触采用R.Vignjevic 等［8］提出的SPH 粒子接触算法。

图5 冲击模型尺寸及离散方式Fig.5 Impact model size and its discretization mode

为描述靶板材料的屈服应力及损伤演化，这里引入T.Børvik 等［9］提出的修正Johnson-Cook 强度模型，该模型将材料的屈服强度表示为损伤变量、等效应变、等效应变率和温度的函数

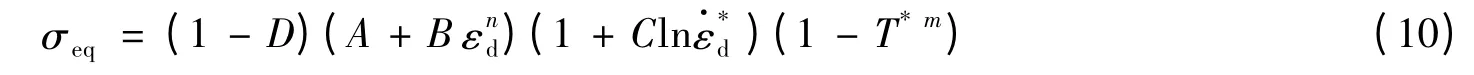
式中:A、B、C、n、m 是材料常数;D 为损伤变量，D=0 表示材料没有损伤，D=1 表示材料完全失效;εd是等效累积损伤塑性应变是等效累积塑性应变是用户定义参考等效应变率;量纲一温度T*=(T－T0)/(Tm－T0)，T0是室温，Tm是材料熔点。实际上材料出现宏裂纹时，损伤变量的临界值小于1，失效准则可描述为D=Dc≤1，其中Dc是损伤变量临界值。损伤变量D 是等效累积塑性应变ε 的函数，可描述如下

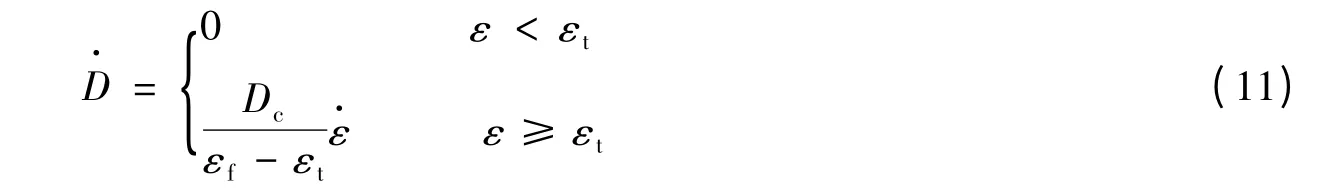
式中:εt是损伤阈值，εf是等效断裂塑性应变，与材料的应力三轴度、应变率和温度相关。G.R.Johnson和W.H.Cook［10］提出的剪切损伤演化模型中将εf描述如下

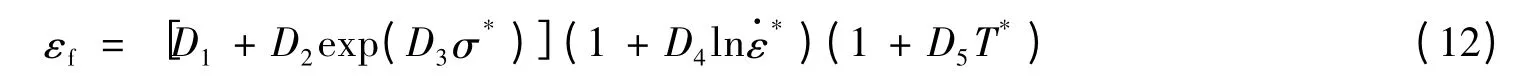
式中:D1～D5为材料常数，σ*=σm/σeq为应力三轴度，σm=(σx+σy+σz)/3 为平均正应力。假设材料处于绝热状态，靶板材料温度的升高是由于冲击过程中的塑性功转换为热量造成的，温度的变化计算为

式中:ρ 为材料密度，cp为材料比定压热容，α 为比例常数，Wp为塑性功。靶板材料参数见表1，靶板压强采用Grüneisen 状态方程计算。

子弹冲击过程中变形较小，采用线弹性模型，材料参数为:E=200 GPa，ν=0.33，ρ=7.838 t/m3。

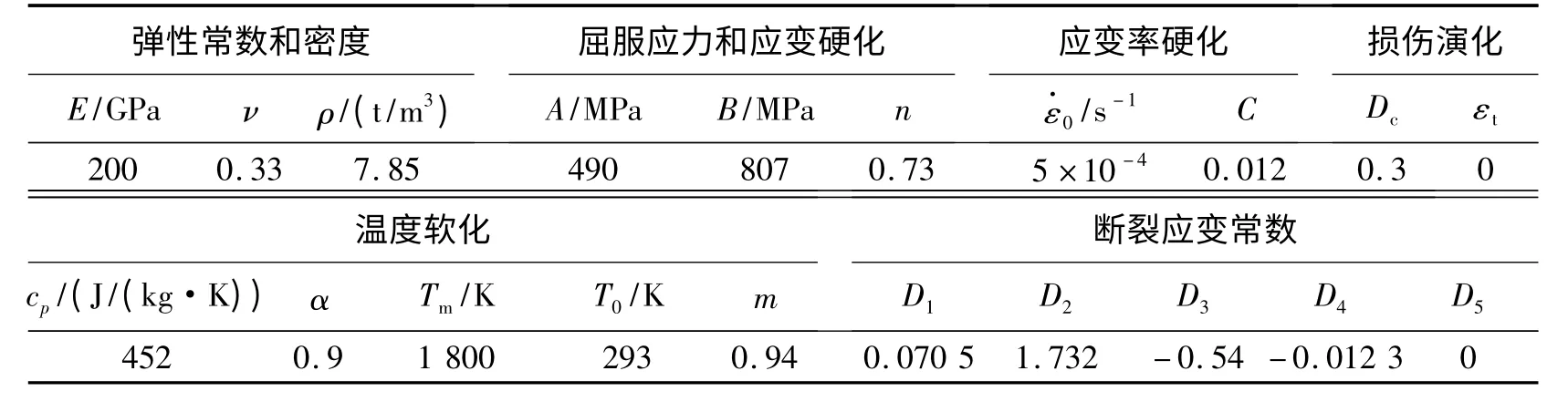
表1 靶板材料参数Table 1 Material parameters of target

当子弹初速v0=285.4 m/s 时，其数值计算结果如图6 所示，子弹、靶塞以及靶板冲塞型破坏的实验结果如图7 ～8 所示［9］。从图中可以看出，计算结果与实验结果吻合很好。在t=7 μs 时，子弹与靶板接触，弹头正前方处的靶板开始加速，靶板被挤压产生压缩变形。之后在弹头周围的靶板出现剪切区，由于接触部位较大的塑性应变，剪切区域内粒子的损伤变量迅速演化，达到临界值，部分粒子完全失效，裂纹逐渐向靶板后部扩展。在冲击后期，失效模式同时包含靶板内部的剪切断裂和靶板背面的拉伸损伤，在t=120 μs，靶塞在子弹的推动下与靶板完全脱离。

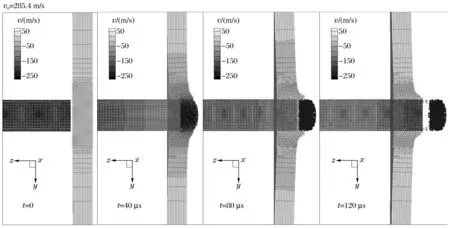
图6 冲击过程的数值模拟结果Fig.6 Numerical simulations of the impact process

图7 冲击后的子弹和靶塞Fig.7 The projectile and plug after impact

图8 冲击后的靶板横截面Fig.8 The cross section of the target after impact

表2 为不同初速时数值模拟值与实验值的对比，其中vpr是子弹余速，vtr是靶塞速度，df是靶板前部穿孔直径，dr是靶板后部穿孔直径。计算和实验存在的靶板穿孔直径差异，主要是因为当子弹和靶板间距达到2 倍光滑长度时，产生接触力，这些与实际的物理过程不能完全相符。通过加密SPH 粒子设置，可以在一定程度上减少该误差。

表2 计算值与实验值对比Table 2 Comparisons between computed results and experimental data

3 结 论

将SPH 粒子固结在有限单元节点，提出了一种新型SPH-FEM 耦合算法，为SPH 和FEM 的耦合计算提供了一种新的途径。该方法可以在FEM 计算困难的区域用SPH 粒子离散，能够充分发挥SPH 和FEM 的特点:SPH 具有处理大变形问题的优势;FEM 计算精度和效率更高。应用该耦合算法，在SPH粒子的边界区域使用有限单元离散，以有限元方的式施加边界条件，可以解决SPH 施加边界条件的难题。该方法可以方便地推广到FEM 与其他无网格方法的耦合计算，如EFG 和RKPM。

提出的SPH-FEM 耦合算法要求在耦合界面处有限单元的尺寸和SPH 粒子间距保持一致，当计算模型几何形状复杂时，前处理建模比较麻烦。在工程实际中使用该SPH-FEM 耦合算法时，为了降低对前处理建模要求，需要根据耦合界面附近有限元单元的尺寸自动调整耦合界面附近SPH 粒子的光滑长度，这一技术还有待于在今后的工作中进一步深入研究。

［1］ Lucy L B.Numerical approach to testing the fission hypothesis［J］.Astronomical Journal，1977，82(12):1013-1024.

［2］ Gingold R A，Monaghan J J.Smoothed particle hydrodynamics:Theory and application to non-spherical stars［J］.Monthly Notices of the Royal Astronomical Society，1977，181:375-389.

［3］ Johnson G R.Linking of Lagrangian particle methods to standard finite element methods for high velocity impact computations［J］.Nuclear Engineering and Design，1994，150(2-3):265-274.

［4］ Johnson G R，Stryk R A，Beissel S R.SPH for high velocity impact computations［J］.Computer Methods in Applied Mechanics and Engineering，1996，139(1-4):347-373.

［5］ Ferna＇ndez-Me＇ndez S，Bonet J，Huerta A.Continuous blending of SPH with finite elements［J］.Computers＆Structures，2005，83(17-18):1448-1458.

［6］ Monaghan J J.SPH without a tensile instability［J］.Journal of Computational Physics，2000，159(2):290-311.

［7］ 强洪夫，高巍然.完全变光滑长度SPH 法及其实现［J］.计算物理，2008，25(5):569-575.QIANG Hong-fu，GAO Wei-ran.SPH method with fully variable smoothing lengths and implementation［J］.Chinese Journal of Computational Physics，2008，25(5):569-575.

［8］ Vignjevic R，De Vuyst T，Campbell J C.A frictionless contact algorithm for meshless methods［C］∥ICCES，2007，3(2):107-112.

［9］ Børvik T，Langseth M，Hopperstad O S，et al.Ballistic penetration of steel plates［J］.International Journal of Impact Engineering，1999，22(9-10):855-886.

［10］ Johnson G R，Cook W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21(1):31-48.