水中爆炸气泡与水底边界相互作用的水射流现象*

汪 斌，张远平，王彦平

(中国工程物理研究院流体物理研究所冲击波物理与爆轰物理国防科技重点实验室，四川 绵阳621900)

物体在随加速运动的流体平移运动时都会受到一种运动学浮力作用，这个力的大小等于流体运动的加速度与该物体排开流体质量的乘积，这种流体中物体受流体运动而产生的力称为Bjerknes 力［1］。炸药在水中爆炸后产生的气泡在舰船附近脉动时，受流体运动产生的Bjerknes 力，气泡会向舰船运动，宛如气泡被舰船目标所吸引，当气泡收缩到最后阶段时，会在舰船壳体表面溃灭产生水射流。占炸药总能量一半以上的气泡能大量用于形成水射流，对舰船壳体造成巨大的冲击力。目前，水中兵器战斗部对舰船目标的毁伤设计主要考虑冲击波效应，如何充分利用气泡能，特别是气泡与船体相互作用产生的水射流对舰船目标进行毁伤打击，已引起人们极大的关注［2］。

获得水中爆炸气泡脉动水射流形成的直观图像，是开展相关研究的基础。J.R.Blake 等［3］、W.Lauterborn 等［4］、N.A.Pelekasis 等［5］、M.S.Plesset 等［6］利用电火花、激光等在水中产生的气泡开展了气泡水射流对目标的汽蚀现象，得到了水射流产生的临界条件和水射流对目标的汽蚀破坏模式。E.Klaseboer［7］开展了炸药产生的气泡与垂直放置的钢板相互作用水射流现象的实验研究工作，其实验结果已经成为水中爆炸气泡动力学数值模拟的主要参考数据。本文中根据开尔文冲量原理，分析气泡脉动形成水射流的主要影响因素，开展PETN 炸药水中爆炸气泡与钢板相互作用水射流实验，对理论分析结果进行实验验证。

1 实验原理

炸药水中爆炸产生的气泡在自由场脉动时的形状近似为球形，当气泡在靠近固壁面脉动时，受强Bjerknes 力影响，在固壁表面形成水射流。在这种条件下，难以用数学公式对其进行描述。J.R.Blake等［3］提出了利用开尔文冲量的概念来描述流体动态特征，其表达式为

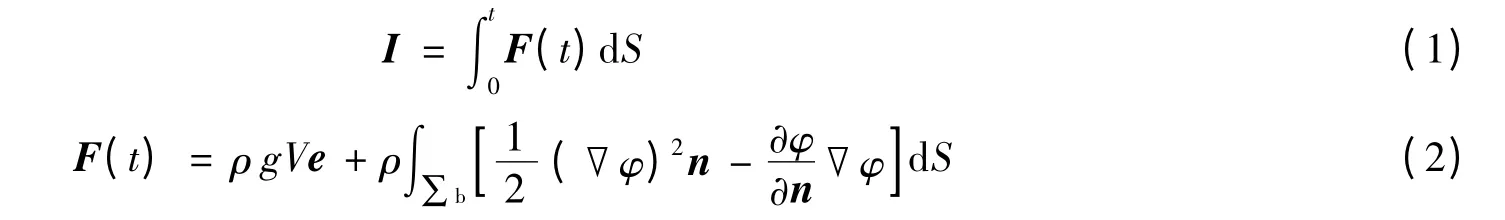
式中:ρ 为流体密度，V 为气泡的体积，e 为浮力方向的单位矢量，φ 为速度势，n 为气泡表面法线方向，S为气泡表面面积，∑表示刚性边界。公式(2)中第1 项表示气泡受到的浮力作用，第2 项表示由刚性壁面引起的流场变化对气泡产生的Bjerknes 力作用，这2 种力的强弱关系决定了气泡的运动方向。公式(2)中第2 项可以用气泡体积随时间的变化表示

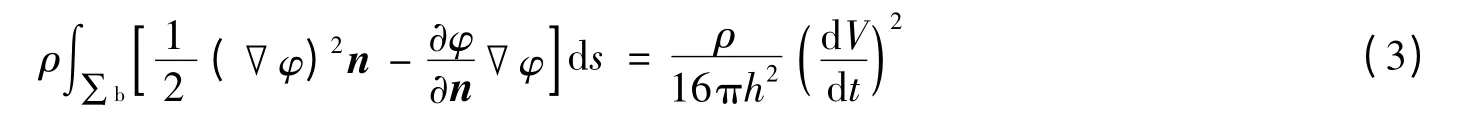
根据气泡半径随时间变化的气泡运动方程

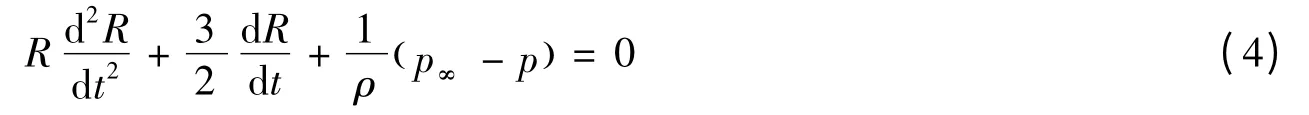
可以得到Bjerknes 的具体表达式

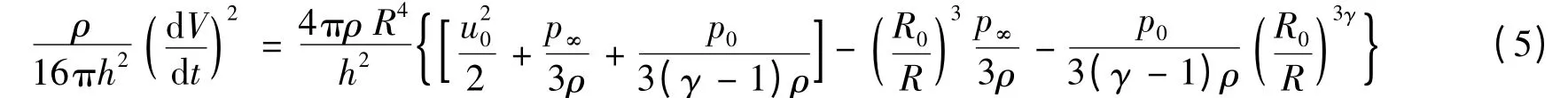
式中:h 为炸药到边界的距离，V 为气泡体积，u0为气泡初始运动速度，R 为气泡半径，p 为气泡内压力，p0为气泡内部初始压力，p∞为水静压，γ 为气泡内绝热指数。在初始条件相同的条件下，Bjerknes 力的大小与h2成反比。即:爆距h 越小，Bjerknes 力越大，对气泡的影响也越大，气泡溃灭产生的水射流会朝向固壁;而随着h 的增加，Bjerknes 力会迅速减小，浮力对气泡的影响占主要地位，气泡脉动过程参数与其在自由场的脉动趋于一致。

2 实 验

实验在2 m×2 m×2 m 的水箱中进行，如图1 所示。将PETN 炸药安装在实验水箱中央，球形超高压短弧氙灯光源发出的光线通过光源窗口进入水箱内部，为高速摄影提供充足的光线，相机幅频为6 300 s－1。高速相机与起爆台、示波器等同步，记录炸药爆炸后气泡产生、膨胀、收缩过程的图像。PCB-138 水下压力传感器距离炸药0.4 m，记录气泡脉动压力。在水深1 m 的条件下，1.5 g PETN 炸药水中爆炸产生的气泡最大半径为19.5 cm［8］，实验时炸药到钢板的距离h 分别为气泡最大半径Rmax的1.4、1.2、1.0、0.8 和0.6 倍。

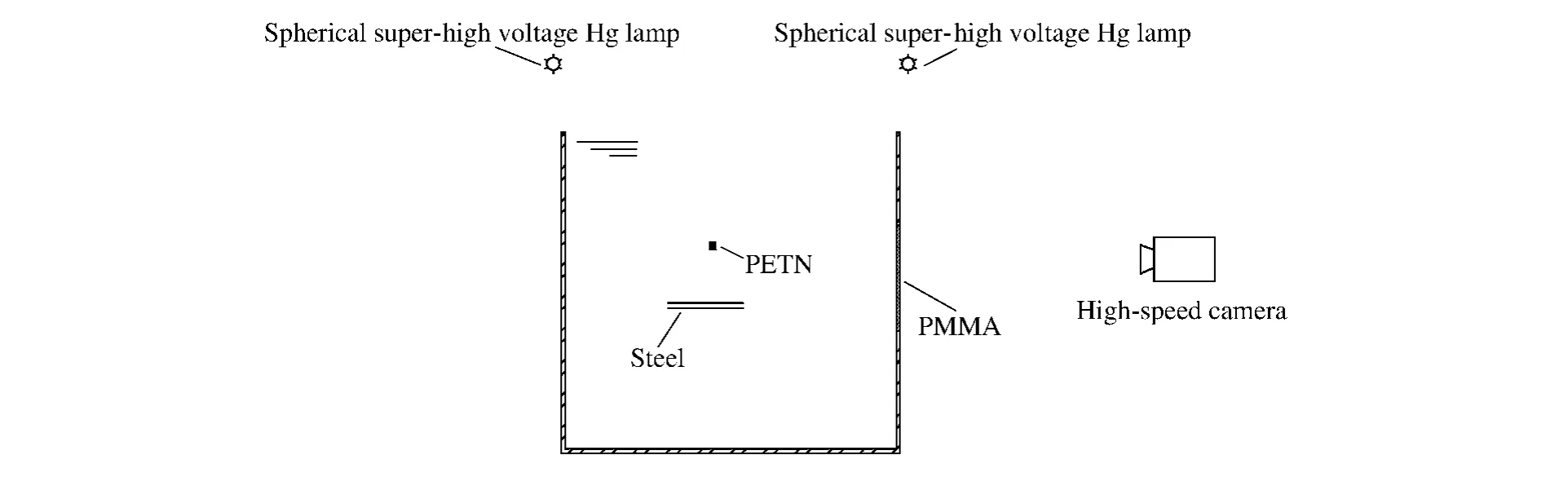
图1 实验装置Fig.1 Experimental apparatus

3 实验结果与分析

3.1 气泡与水底边界相互作用过程图像

图2 给出了爆距h=1.4Rmax时的气泡与水底边界相互作用过程图像，受观测窗口限制，仅能拍摄到部分气泡图像。在第1 次膨胀过程中的形状没有受到边界条件的影响，当气泡收缩时，形状逐渐偏离球形，但仍然保持收缩时同时上浮的现象，这与气泡在自由场脉动过程的现象基本一致［9］，说明气泡脉动过程中受Bjerknes 力的影响较小，浮力在气泡脉动过程中起主要作用，气泡在完成2 次脉动的同时上浮出视场范围。

图3 给出了h=1.2Rmax时气泡与水底边界相互作用过程图像。随着爆距h 的减小，Bjerkens 力对气泡脉动过程开始产生影响。在气泡膨胀阶段，气泡形状仍然保持球形，随着气泡的逐渐收缩，靠近水底边界的部分变得细长，而朝向水自由面方向的气泡曲率低于水底部分，形成卵形(t=28.5 ms)。当t=32.2 ms 时，气泡收缩至最小，然后产生2 次膨胀。气泡收缩膨胀过程没有产生明显的上浮现象，与自由场脉动现象产生明显差异，说明Bjerkens 力在气泡脉动过程中逐渐发生作用，方向与浮力相反，使气泡在原地保持不动。气泡2 次脉动过程(t=32.2 ～56.0 ms)和第3 次脉动过程(t=56.0 ～74.7 ms)与第1 次脉动现象基本一致。当气泡完成3 次脉动后，受气/水界面不稳定性等因素的影响［2］，气泡在第4 次膨胀过程中溃灭形成云雾气团，其形态已不能用球形气泡的形式来进行描述。

图2 h=1.4Rmax时气泡脉动图像Fig.2 Pictures of bubble oscillation

图3 h=1.2Rmax时气泡脉动图像Fig.3 Pictures of bubble oscillation

当爆距h=1.0Rmax时，Bjerknes 力迅速增大，并在气泡脉动过程中一直占据主导地位，气泡与钢板相互作用开始产生水射流现象，如图4(a)所示。气泡在膨胀阶段形状仍然没有发生明显变化，但在膨胀到最大时，靠近钢板一侧的气泡边界已经与钢板相接触。靠近钢板处的水由于钢板向下运动产生负压，使水产生空化现象，图中可以很清晰地看到钢板表面的白色气泡团。随着气泡的收缩，受Bjerknes力的影响，靠近钢板一侧的气泡形状曲率较其相反面有明显变化，形成一个橄榄形(t=30.5 ms)。当气泡收缩至最小时，由于表面受力不均匀，导致气泡溃灭产生水射流现象。由于吸引气泡向下运动的Bjerknes 明显大于向上的浮力，使水射流方向朝向钢板表面，高速摄影判读的水射流到达钢板表面的速度为120 m/s。当水射流到撞击钢板表面以后，气泡形状已经发生明显变化。

爆距h=0.8Rmax时的气泡与边界相互作用水射流现象与爆距h=1.0Rmax的现象基本一致，由于炸药距离更接近钢板，因此Bjerknes 力更大。在气泡收缩阶段，其表面已经紧贴钢板，在表面产生水射流现象，如图4(b)所示。当爆距进一步减小到0.6Rmax时，Bjerknes 力在气泡脉动过程中占据主导地位，气泡与钢板相互作用，水射流现象变得越来越明显，如图4(c)所示。气泡在初始膨胀阶段就已经紧贴钢板，在收缩阶段，气泡吸附在钢板壁面。气泡收缩形成水射流时，可以观察到水射流形成过程迹线。从不同爆距条件下的气泡与钢板相互作用实验可以看出:Bjerknes 力的大小与爆距密切相关，爆距越小，Bjerknes 力越大，对气泡脉动水射流形成过程的影响也逐渐增加。

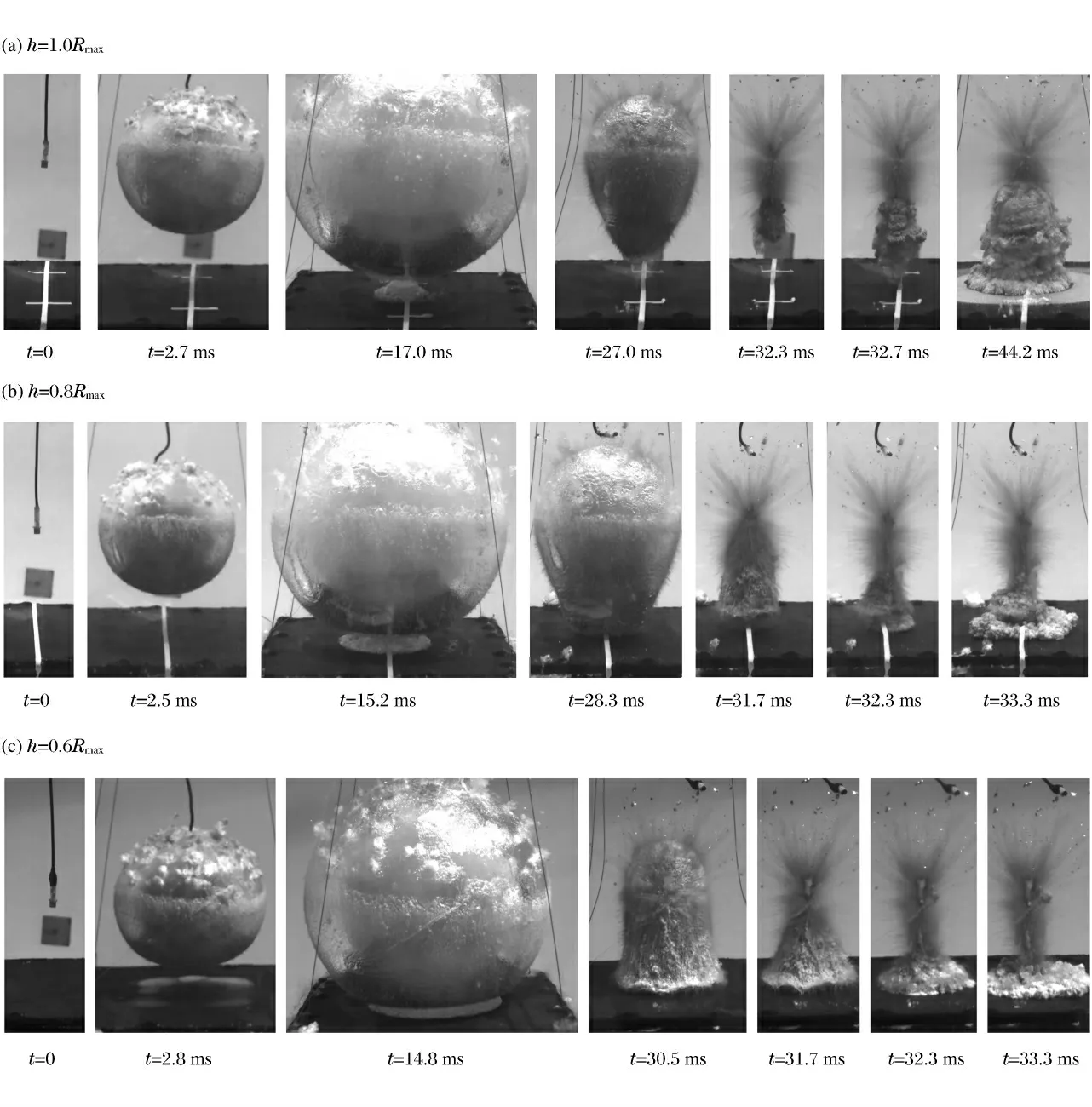
图4 气泡与边界相互作用水射流形成过程图像Fig.4 Pictures of the water jet formed during bubble-interaction

3.2 水中爆炸压力

在不同爆距条件下，水中压力传感器记录的冲击波峰值压力没有发生明显变化，但是气泡脉动周期和压力发生明显变化，如图5(a)所示，气泡脉动压力局部放大后见图5(b)。随着爆距的减小，气泡脉动周期随之减小，而气泡脉动压力有较大差异。根据水中爆炸气泡能计算公式［9］

在实验条件一定时，静水压力pH和水密度ρ0相同，因此气泡能Eb的大小仅与气泡脉动周期Tb有关。实验中，随着爆距的减小，气泡脉动周期减小，气泡能减小。本轮实验采用相同的炸药，因此不可能存在气泡能减小的问题，造成气泡脉动周期减小的原因主要受边界条件的影响，当存在Bjerknes 力时，气泡脉动过程受到的不稳定性因素增加，加速气泡溃灭，导致气泡脉动周期减小。

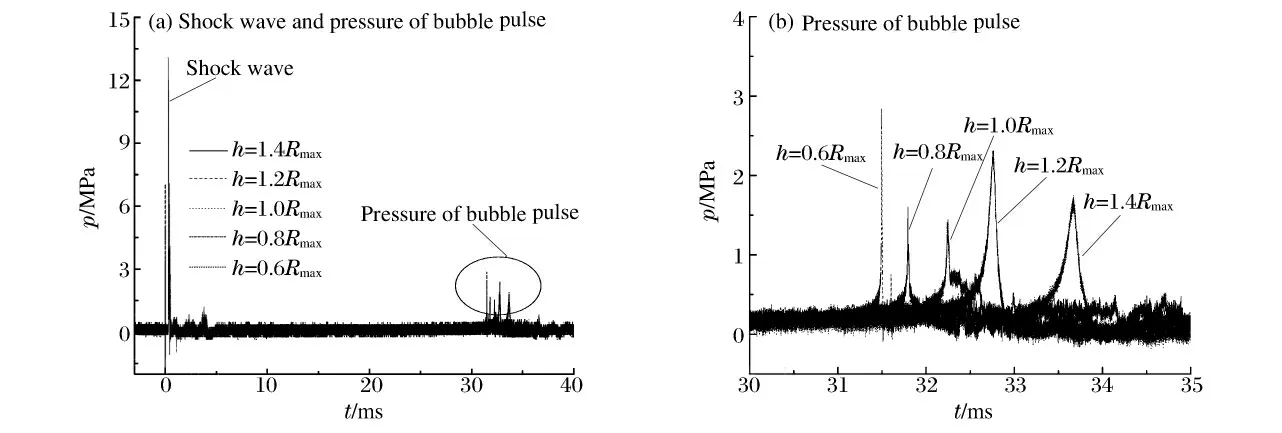
图5 压力测试结果Fig.5 Results of pressure

4 结 论

(1)在气泡位于水平放置的钢板上方条件下，爆距h ＞1.4Rmax，浮力对气泡脉动过程起主要作用，随着爆距的减小，Bjerkens 力迅速增大;当h=1.2Rmax时，Bjerkens 力与浮力基本相当;当h ＜1.0 Rmax时，Bjerknes 力在气泡脉动过程中起主要作用，气泡与边界相互作用产生水射流现象。

(2)受Bjerknes 力影响，气泡脉动周期随爆距的减小而减小。

(3)气泡溃灭产生的水射流具有非常明显的方向性，对目标具有一定的毁伤作用。

［1］ Bjerknes V F K.Fields of force［M］.Columbia:Columbia University Press，1906.

［2］ Strahel W C.Conventional weapons underwater explosions［R］.AD-A201 814，1988.

［3］ Blake J R，Taib B B.Transient cavities near boundaries.Part 1.Rigid boundary［J］.Journal of Fluid Mechanics，1986，170:479-497.

［4］ Lauterborn W，Bolle H.Experimental investigations of cavitations-bubble collapse in the neighborhood of a solid boundary［J］.Journal of Fluid Mechanics，1975，72(2):391-399.

［5］ Pelekasis N A，Tsamopoulos J A.Bjerknes forces between two bubbles［J］.Journal of Fluid Mechanics，1993，254(3):467-499.

［6］ Plesset M S.Bubble dynamics and cavitation［J］.Annual Review of Fluid Mechanics，1977，9:145-185.

［7］ Klaseboer E，Hung K C.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure［J］.Journal of Fluid Mechanics，2005，537:387-413.

［8］ 汪斌，王彦平.有限水域气泡脉动实验方法研究［J］.火炸药学报，2008，31(3):32-35.WANG Bin，WANG Yan-ping.A method of studying bubble pulse in a confined water area［J］.Chinese Journal of Explosives＆Propellants，2008，31(6):32-35.

［9］ Cole P.Underwater explosions［M］.Princeton:Princeton University Press，1946:162-169.