具有脉冲出生及垂直传染的SIS传染病模型的全局稳定性
2011-02-20曹文军
曹文军
(中北大学数学系, 山西 太原 030051)
0 前 言
控制传染病一直是当今世界迫切需要解决的一个重大问题,尤其对于濒临灭绝的动物种群来说更为重要.传统的传染病模型[1,2]总是假设种群个体的出生是连续的,而实际中对于像鳄类等野生动物来说其出生是集中在某个季节进行的,采用具有脉冲出生的模型[3-5]来研究更为符合实际.
本文主要针对此类种群建立了一类具有脉冲出生并同时考虑垂直传染(母体将病先天传染给新生儿)的SIS模型.
(1)
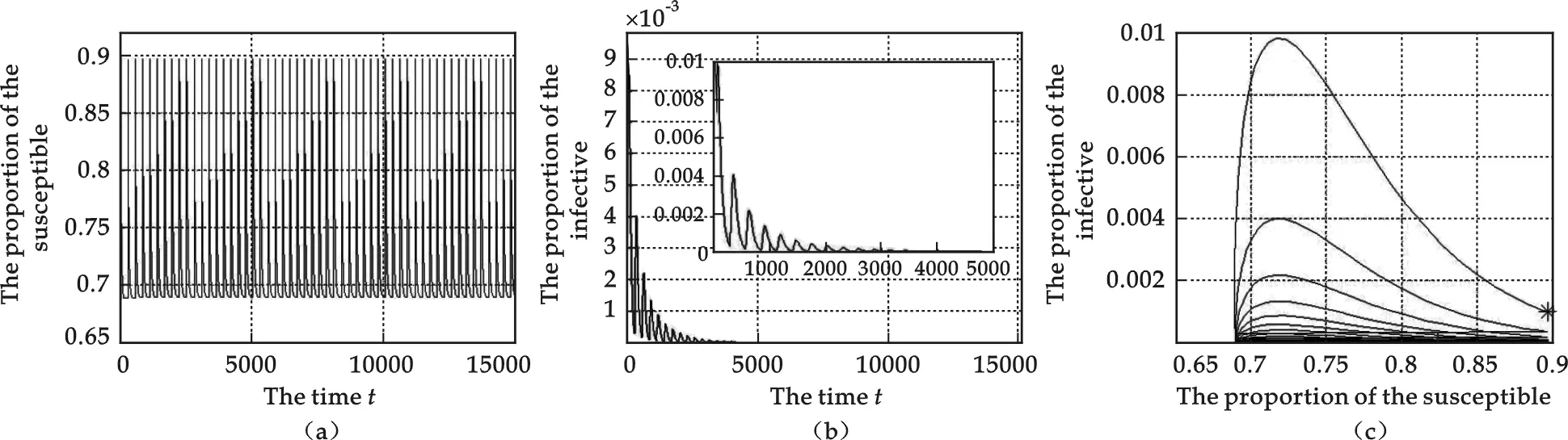
其中,S和I分别表示易感者和染病者的个体数量,参量β表示有效接触率,d表示自然死亡率,γ表示恢复率,α表示因病死亡率,b表示种群的出生率,p(0 种群中个体总数记为N,即N=S+I.从系统(1)可知: (2) 考虑到模型的生物学意义,易知Ω={(S,I)|S≥0,I≥0}是系统(1)的正向不变集. 疾病不存在时,即I(t)=0.此时,易感者满足方程 (3) 在区间nT (4) 易得λ2<1当且仅当基本再生数R0<1. 证明 为了研究方便,我们利用N=S+I将系统(1)化为下述形式: (5) 根据脉冲微分不等式[7]得到 (6) 对于系统 利用脉冲微分不等式,对于t∈[T1+nT,T1+(n+1)T]可得 (7) (8) (9) 因为 (10) 下面将利用Matlab给出系统(1)基本再生数R0<1和R0>1时一些数值模拟,两组图中(a)和(b)分别表示易感者和染病者的时间序列,(c)表示S-I相图,其中参数A=0.02、β=0.6、d=0.029、γ=0.4、α=0.002、b=0.3及p=0.7.图1 中易感者和染病者的初值分别为S(0)=0.896 6,I(0)=0.001,且取周期为T=280,基本再生数R0=0.997 1<1.图2中易感者和染病者的初值分别为S(0)=0.913 0,I(0)=0.001,且取周期为T=100,基本再生数R0=1.065 5>1.由图可以看出当R0<1疾病最终会消除,而R0>1时疾病持续. 图1 当R0<1时系统 (1) 的解轨线 图2 当R0>1时系统 (1) 的解轨线 本文建立了一类具有脉冲出生及垂直传染的SIS传染病模型,利用频闪映射得到其无病周期解的存在性,通过Floquet乘子理论及脉冲微分不等式得到无病周期解当基本再生数R0<1时是局部并且是全局渐近稳定的,最后利用数值模拟验证了理论结果,并且由该部分结果可以发现当R0>1时无病周期解不稳定,疾病将会持续.该模型主要适用于数量在不断下降但可以有外界的补充来保证其不会灭绝且具有脉冲出生的种群,例如濒临灭绝的种群,像我国的扬子鳄,由于自然环境恶劣及人类的滥杀滥捕导致他们的数量急剧下降,为了保证其不走向灭绝,国家采取人工繁殖饲养对其数量进行补充;或者也适用于生活在某个环境比较恶劣(比如食物缺乏等等)的地区的种群,而它们又有比较便利的条件来摄取少许资源以维持自己种群不致灭绝,如所生活地区邻近资源丰富地区或可选择替代的食物等等. 参考文献 [1] 靳 祯,马知恩.具有连续和脉冲预防接种的SIRS传染病模型[J].华北工学院学报,2003,24(4):235-243. [2] 靳 祯,马知恩,原三领.总人口在变化的SIR流行病模型[J].工程数学学报,2003,20(3):93-98. [3] M.G.Roberts, R.R.Kao. The dynamics of an infectious disease in a population with birth pulses[J]. Math. Biosci., 1998,(149):23-36. [4] Shujing Gao, Lansun Chen, Lihua Sun. Dynamic complexities in a seasonal prevention epidemic model with birth pulses[J]. Chaos,Solitons and Fractals, 2005,(26):1 171-1 181. [5] Wenjun Cao, Jin Zhen. The dynamics of the constant and pulse birth in a SIR epidemic model with constant recruitment[J]. Journal of Biological Systems, 2007,15(2):203-218. [6] 靳 祯.在脉冲作用下的生态和流行病模型的研究[D]. 西安:西安交通大学博士论文,2001. [7] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].第一版,北京:科学出版社,2004:303-306.1 无病周期解的存在性

2 无病周期解的局部稳定性
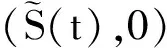
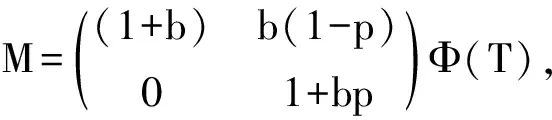
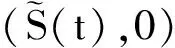
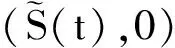
3 无病周期解的全局稳定性
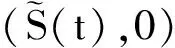

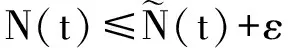





4 数值模拟

5 结论
