考虑碳排放控制的多种运输方式组合优化模型研究
2011-02-20罗诚
罗 诚
(上海交通大学中美物流研究院, 上海 200030)
0 引 言
交通运输行业作为能源消费增长最快的行业,对控制温室气体排放具有重要的影响,因此国内学者在运输行业如何控制碳排放方面开展了不少研究.黄大雷[1]针对运输工具使用石化燃料产生的碳排放,提出了减少单位吨公里运输工具的排放量和减少无效的吨公里两种思路.纪念[2]围绕提高现有交通运输体系能效、减少能源需求、降低温室气体排放等议题,为中国交通运输业发展“低碳经济”提供了政策建议.总结相关研究可以发现,对于运输业控制碳排放的相关研究大都集中在技术改进和政府政策方面,而对企业在运输决策中如何合理的考虑碳排放控制则研究较少.
在企业运输活动中,运输方式的不同直接影响到运输成本、时间和碳排放量等要素,而传统的运输方式选择多目标优化问题往往只考虑运输成本和运输时间两个目标函数[3-5],对不同运输工具在运输过程中产生的碳排放量大小并没有考虑,也就是说相关模型并没有考虑不同运输方式的环境指标对运输方式决策的影响.本文创新性的提出了考虑碳排放控制的多种运输方式选择多目标规划模型,然后介绍了该模型的解法并进行了示例计算,为企业在考虑碳排放控制情况下的运输方式选择决策提供了可行思路.

图1 虚拟运输网络图
1 考虑碳排放控制的多种运输方式组合优化模型
1.1 问题与模型的提出
设有一多种运输方式组合优化问题:将一批货物从起始地O运送到目的地P,途中经过N个城市,任意相邻的两城市间有K种运输方式,各运输方式的运输时间、费用和碳排放情况不同,当运输方式在相邻城市间转换时需要一定的中转时间和费用并产生一定量碳排放,问如何选择运输方式组合,使运输总费用尽量低、总时间尽量短、碳排放量尽量少?
为了更直观地描述问题,用一个虚拟运输网络图(图1)对上述问题进行描述,方法如下[3]:
(1)除O和P外,其他各城市分别扩展为2K个城市节点.对于城市A,其中左侧K个节点A11、A12、…、A1K分别表示K种运输方式的输入节点,右侧K个节点A21、A22、…、A2K分别表示K种运输方式的输出节点;(2)各条弧上的权重分别为费用权重、时间权重和碳排放权重;(3)终点P再扩展K个输入节点,Pi到P之间的时间、费用和碳排放均为0.
在上述多种运输方式选择组合优化问题中,要同时兼顾降低运输总费用、缩短运输总时间和减少总的碳排放量3个目标,其数学模型可描述为一多目标规划模型:
(1)
(2)
(3)
约束条件:

(4)
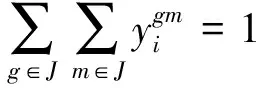
(5)
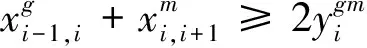
(6)
(7)
(8)
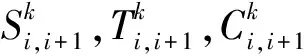
1.2 求解模型的逐步法(STEM)
当所有目标函数和约束条件为线性时,对于多目标规划有些特殊的解法,特别是泽勒内(Zeleny)等将解线性规划的单纯形法给予适当修正后,用来解多目标线性规划问题[7],其中逐步法(STEM)是一种迭代法,解法如下:
设有k个目标的线性规划问题:

求解的计算步骤为:
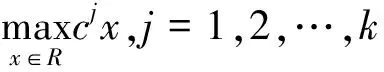
为了找出目标值的相对偏差以及消除不同目标值量纲不同的问题,进行如下处理:

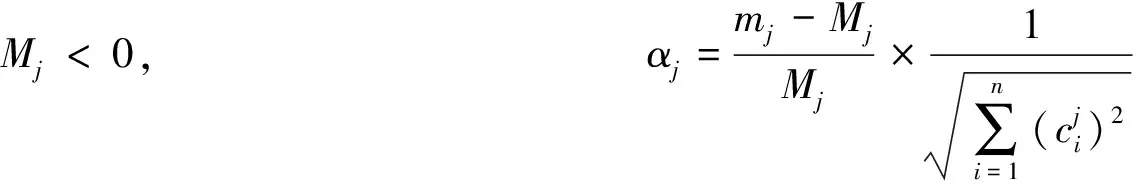
第三步:构造以下线性规划问题,并求解.
并令第j个目标的权系数πj=0,表示降低这个目标的要求,再求解以下线性规划问题:
2 应用示例计算
将一批货物从城市O运到城市P,途经A市,相邻两个城市之间都有汽车、轮船和飞机3种运输方式可供选择,其有关参数如表1和表2所示,问如何选择运输方式组合,可以达到总费用、总时间和碳排放都尽量少的目标?

表1 各个城市间的运输费用、时间和碳排放表(费用/时间/碳排放)

表2 不同运输方式中转费用、时间和碳排放表(费用/时间/碳排放)
建立多目标线性规划模型:

3 结束语
在人为温室气体排放日益加剧的背景下,碳排放相关问题已经成为学术界研究的重点及企业运作实践中格外关注的问题之一.本文基于多种运输方式组合问题,在考虑碳排放因素的前提下,建立了运输方式组合选择多目标规划模型,定量分析了运输方式选择决策问题,然后提出了求解这一多目标规划的逐步法解法,并假定决策情景,给出了模型的应用示例计算.
模型的建立与相应的求解方法,对运输企业在成本与时间可接受的情况下选择符合碳排放控制要求的运输方式提供了科学的指导,对企业在运输方式选择时如何实施碳排放控制策略具有一定的参考意义.
进一步的研究可以将问题扩展到运输网络优化与运输方式选择相结合建立优化模型的情形,这对运输过程中实施碳排放控制策略具有更大的意义.
参考文献
[1] 黄大雷. 运输企业的碳足迹和绿色供应链管理[J]. 物流技术与应用, 2009,43(3): 71-72.
[2] 纪 念. 交通运输业发展“低碳经济”之路怎样走[J]. 环境保护,2010,29 (10): 62-64.
[3] 井祥鹤, 魏冬峰, 周献中. 运输方式选择多目标优化问题的混合遗传算法[J]. 计算机工程与应用, 2008,44 (6): 210-214.
[4] 高更君, 黄 卫. 考虑时间因素的运输方式选择问题[J]. 交通运输系统工程与信息,2001,2: 63-66.
[5] 刘 舰, 俞建宁. 多式联运运输方式选择的模型和算法[J]. 兰州交通大学学报, 2010,29(1): 56-61.
[6] 运筹学教材编写组. 运筹学(修订版)[M]. 北京:清华大学出版社,1990:457-458.
