甚长基线的双基地机载雷达杂波建模与分析
2011-02-20姬妍
姬 妍
(榆林学院能源工程学院, 陕西 榆林 719000)
0 引 言
甚长基线的双基地雷达对地面进行探测时,接收到的回波数据中会有很强的地面杂波干扰存在,地面动目标信号常常会淹没在其中,这对地面动目标的检测带来了很大的挑战.与单基地雷达相比,双基地雷达的杂波分布[1,2]受两载机配置(发射和接收平台的速度、高度、飞行方向与阵面轴线的夹角等)的影响分布非常复杂.甚长基线的双基地雷达对处在平台之间和之外的地面动目标进行检测,杂波的分布形状不仅和平台的配置参数有关,而且地面杂波在发射和接收载机平台在地面上投影点之间和之外的杂波差异也比较大,因此对于甚长基线这种新的机载双基地雷达体制,杂波模型[3-5]的准确估计直接影响到系统对于地面杂波的抑制性能[6]以及空时自适应处理的动目标的检测性能[7-9].

图1 杂波模型图
本文建立了在甚长基线配置模式下杂波的一般模型,给出了杂波的距离多普勒和方位多普勒的准确表达式,分析了处在此区域杂波的特点及其产生的原因,并通过计算机仿真验证了模型的正确性,为甚长基线新的配置模式下的杂波抑制和运动目标检测研究奠定了基础.
1 甚长基线的双基地雷达杂波建模
图1给出了一般双基地机载雷达的几何关系.假定地面水平,以发射载机和接收载机之间的连线在地面上的投影作为X轴,建立OXYZ坐标系;T、R分别表示发射载机和接收载机,它们的坐标分别为(Tx,Ty,Tz)和(Rx,Ry,Rz);S表示地面杂波散射点;C表示等距离椭圆环的中心;Ra和Rb分别表示距离环的中心点与发射载机和接收载机在地面上投影的距离;RT和RR分别表示杂波散射点距离发射载机和接收载机的距离;VT和VR分别表示发射载机和接收载机的飞行速度;HT和HR分别表示发射载机和接收载机的飞行高度;θFT和θFR分别表示发射和接收天线相对于基线方向的方位角;δT=0°和δR=0°情况下,δR为发射载机和接收载机的飞行方向与基线方向的夹角;θs为距离环上的散射点和距离环中心连线与基线的夹角;φT和φR分别表示杂波散射点相对于发射载机和接收载机的俯仰角;ψT和ψR分别表示杂波散射点相对于发射载机和接收载机飞行方向的夹角;θAT为发射天线阵面的轴向与发射载机飞行方向的夹角;θAR为接收天线阵面的轴向与接收载机飞行方向的夹角;由发射机T和接收机R组成机载系统;地面回波数据为接收机接收的等距离环上所有回波数据的总和,这些等距离环是由T和R所构成的椭球与XOY平面的交线构成(图1中虚线椭圆).当发射和接收距离之和为Rs时,由T和R组成的椭球方程[4]为:
(1)
化简得:
b2(xcosβ+zsinβ-εx)2+a2y2+a2(-xsinβ+zcosβ-εz)2=a2b2
(2)
该椭球与XOY平面相交的椭圆方程为:
b2(xcosβ-εx)2+a2y2+a2(xsinβ+εz)2=a2b2
(3)
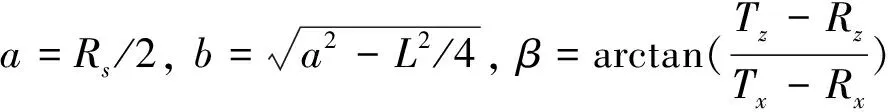
(4)
(5)
在发射机T和接收机R在地平面上投影点之间的杂波区域处,θFR的范围不再是(0,2π),因此不能以接收的方位角作为建模参数.本文通过计算椭圆中心点C的坐标,由于C点和杂波散射点S的连线与X轴的夹角θs的范围为(0,2π),因此可以用θs建立方程来求解RR和RT.由上面的椭圆方程可以求出椭圆中心点C的坐标为:
(6)
当椭球和XOY平面相切,这时可以得到最小距离环的距离:
(7)
对于同一个距离环内的杂波有:
RR+RT=Rs
(8)
由杂波模型的几何关系可得:
(9)
化简得:
A·R2+B·R+C=0
(10)
其中:
(11)
由式(10)求解R,发射和接收的距离、方位角和俯仰角可以用R表示:
(12)
杂波的空域角频率和时域角频率分别为:
(13)
式中λ为雷达发射信号的波长,fprf是雷达的脉冲重复频率.
其中:
cosψR=cos(θFR-δR)cosφR, cosψT=cos(θFT-δT)cosφT
cosψFR=cos(θFR-δR-θAR)cosφR, cosψFT=cos(θFT-δT-θAT)cosφT
(14)
cl(n,k)为对于第n路(列子阵)第k个脉冲的对第l个距离环接收的杂波数据(忽略噪声项),考虑等效阵元方向性和距离调制,则有:
(15)
对于无模糊系统,第l个距离环的杂波数据的协方差函数为:
(16)

图2 几种简单的飞行模式
其中,Δn=n2-n1,Δk=k2-k1,gn(φR)为第n个天线的接收方向图函数,F(θT,φT)为发射方向图函数.
在双基地雷达系统中,发射和接收的载机平台的配置模式有无穷多种,而对于研究双基地雷达杂波分布而言,其中4种载机平台的配置模式比较典型,如图2所示.
2 甚长基线的双基地雷达杂波仿真
不失一般性,我们假定发射和接收都为正侧视情况下,系统的配置参数如表1所示.
图3按照表1中的配置参数仿真了图2中4种典型的飞行模式下处于发射和接收平台之间与之外杂波分布的杂波方向-多普勒图,发射和接收平台之间(208.806 1 km
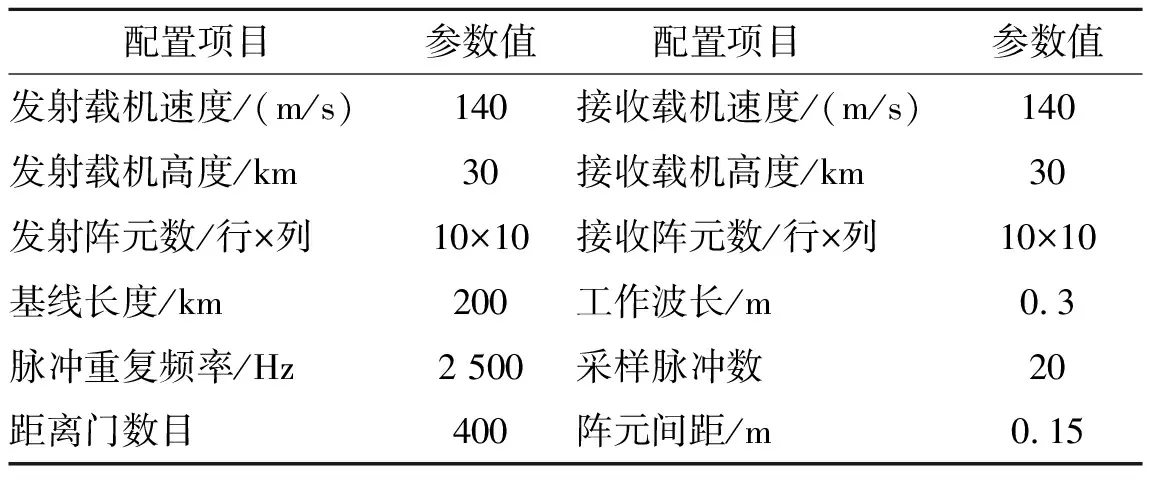
表1 系统的配置参数
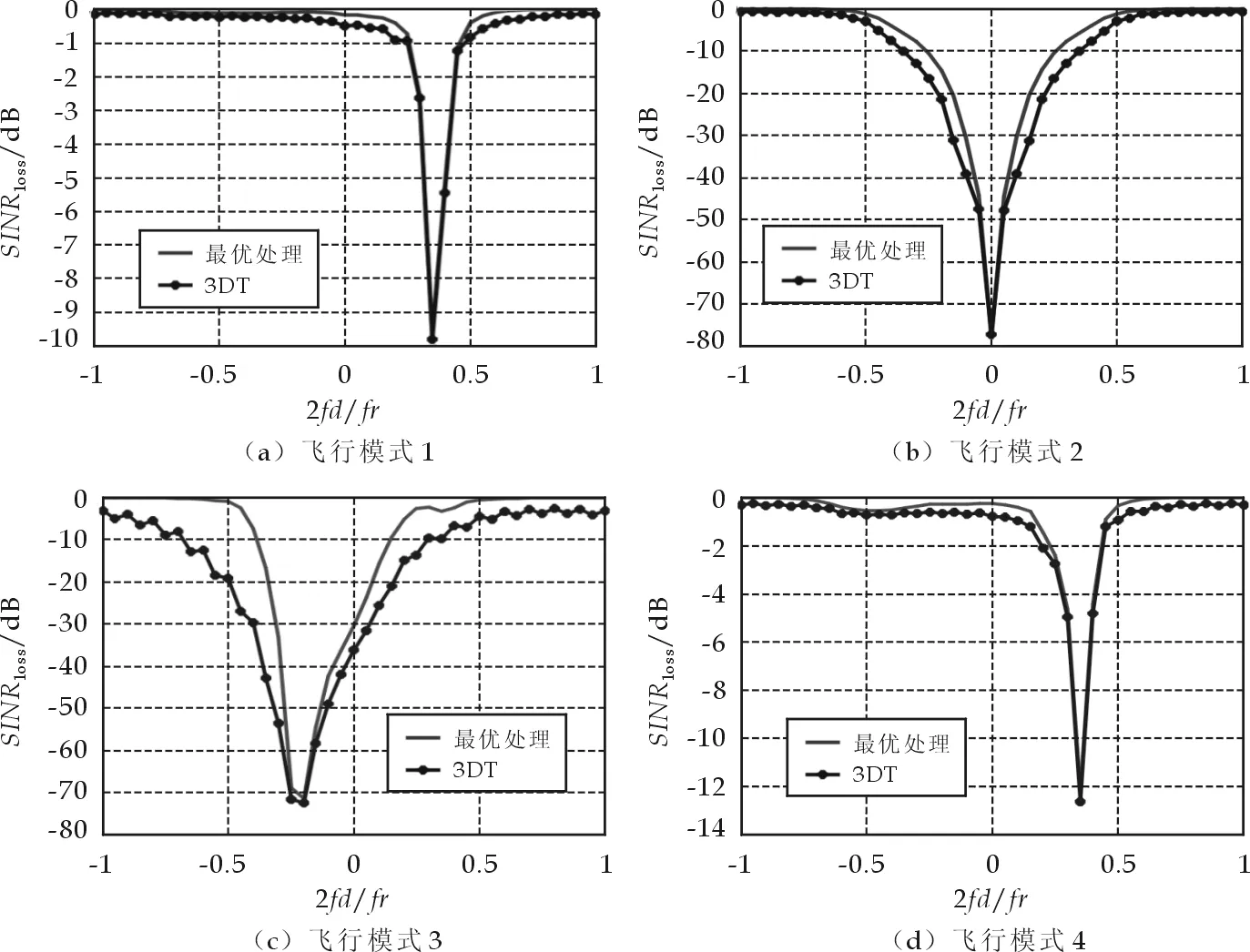
图3每种飞行模式的仿真图中,3个距离环(Rs分别为205 km,220 km,250 km)杂波分布形状近似,但并不重合,这是由于同一距离环的杂波可以看成是以发射和接收载机为焦点的椭球与地平面(假设地平面水平)相交所形成的椭圆.由式(3)及(4)知,对于不同的距离环,这样的椭圆也不相同,导致了不同距离环上的杂波分布也不相同,这说明杂波具有距离依赖性.从仿真结果可知,在甚长基线配置模式下,双基地雷达在不同的载机飞行模式下杂波形状差异很大,这主要是由于不同的飞行模式导致天线轴向和载机飞行方向之间的夹角有很大的不同,进而导致杂波分布的形状有很大的差异.载机平台之间区域的杂波与平台之外的杂波在分布形状上差异也比较大,对于处在发射和接收平台之间(200 998 m 图4~图7分别给出了在图2 4种飞行模式下的杂波功率谱亮度图.图(a)中发射和接收平台之间(208.806 1 km 图3 4种典型的飞行模式下的方向-多普勒图 图4 飞行模式1下的杂波功率谱亮度图(主波束方向θs=90°) 图5 飞行模式2下的杂波功率谱亮度图(主波束方向θs=0°) 图6 飞行模式3下的杂波功率谱亮度图(主波束方向θs=0°) 图7 飞行模式4下的杂波功率谱亮度图(主波束方向θs=0°) 由图4~图7可见,杂波的功率谱亮度图是由顺次相邻的400个距离环积累形成的杂波功率在方位和多普勒方向上的分布,杂波的功率谱分布形状和杂波在方位和多普勒图上的分布一致,这验证了本文中的模型的正确性.另外,由于杂波分布具有距离依赖性,杂波的功率谱分布也发生了明显的展宽,这使得使用带检测距离单元临近的距离环来估计检测单元的杂波谱分布不准确. 图8 4种飞行模式下的空时处理性能 图8分别给出了在图2 4种飞行模式下的空时处理性能,分别采用了全维最优处理方法和3_DT降维处理方法. 甚长基线的机载双基地雷达是一种全新的雷达体制.本文主要研究了在这种体制下的杂波分布模型.通过计算机仿真,发现在甚长基线的配置下杂波分布随载机平台的飞行模式变化很大.另外,杂波具有较强的距离依赖性,杂波在载机平台之间和之外区域的分布差异也比较大.在4种典型的双基飞行模式下,发射和接收飞机一前一后的飞行模式对于动目标检测比较有利,它的空时自适应处理的信干噪比损失比其他几种模式小.甚长基线的机载双基地雷达杂波分布模型的建立为今后研究这一全新体制雷达的杂波抑制和地面目标检测奠定了基础. 参考文献 [1] Himed B. Effects of bistatic clutter dispersion on STAP systems[J].IEE Proceedings on Radar,Sonar and Navigation, 2003, 150(1):28-32. [2] Zhang Y, Himed B. Effects of geometry on clutter characteristics of bistatic radars[A].2003 IEEE Radar Conference[C] .USA: IEEE, 2003,(10): 417-424. [3] Hartnett M P. Ground and airborne target detection with bistatic adaptive space based radar[A]. Proceedings of IEEE Radar Conference[C]. USA: IEEE, 1999. [4] 王永良,彭应宁.空时自适应信号处理[M].北京:清华大学出版社,2000. [5] 王永良,魏进武,陈建文.双基地机载雷达空时二维杂波建模及杂波特性分析[J].电子学报,2001,29(12):1 940-1 943. [6] 吴 洪,王永良.双基地机载预警雷达建模与分析[J].电子学报,2006,12(12):368-375. [7] 李 华,汤 俊,彭应宁.星载双基地雷达空时二维杂波建模方法[J].电子学报,2008,36(3):418-430. [8] 孟祥东,吴建新,王 彤,等.机载双基雷达杂波分析及其距离模糊杂波的抑制[J].西安电子科技大学学报,2008,35(6):992-998. [9] 王万林,廖桂生,张光斌.相控阵AEW雷达杂波抑制的非均匀处理方法研究[J].电波科学学报,2004,19(3):348-353.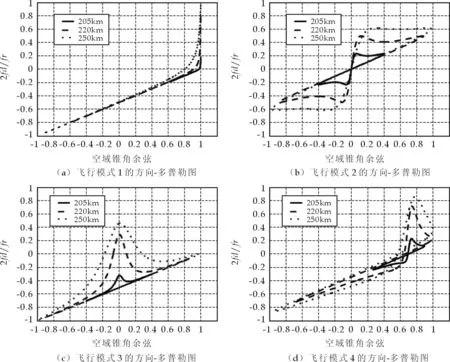




3 结束语
