斜交角变化对斜交弯梁桥结构内力影响的计算分析

张 彧， 张 慧， 马佳铮

(1．兰州交通大学 交通运输学院，甘肃 兰州 730070;2．北京交通大学 土木建筑工程学院，北京100032;3．兰州大学 经济管理学院，甘肃 兰州 730030)

自20 世纪80 年代以后，为了满足复杂条件下道路桥梁布线要求，斜弯桥采用的越来越多。而斜弯桥设计与施工对工程部门提出了许多新的难题［1-4］。目前设计部门运用通用结构程序来分析斜弯桥结构的内力时，通用程序并不能有效地解决边界条件问题，结构动力分析也较难以实现［5-6］。故对斜弯桥诸多问题如设计理论与方法、结构的力学行为、构造特点、施工技术等问题的解决就显得非常必要［7-8］。

1 斜交弯梁桥的建模

计算以实际工程为依托，采用不改变跨径和曲线半径，调整斜交角的方式，计算斜交角选取了15°、30°、45°和60°的一组数据进行对比。这样基本上包括了工程上一般斜桥斜交角的变化范围，计算结果具有一定的适用性。鉴于各种模型本身的特点以及分析侧重点不同，采用板单元建模进行有限元分析。

以某三跨预应力混凝土连续刚构箱梁桥为原型［9］，材料参数如表1，并加入斜交梁段进行有限元建模计算。上部结构为44 +72 +44 m，共160 m 连续刚构斜交弯箱梁，墩高30 m，曲率半径450 m，斜交角分别取15°、30°、45°和60°。

表1 材料参数

模型采用有限元分析程序ANSYS 中的she1163，link8 和solid45 模拟。Shel163 为弹性三维板单元，有弯曲和薄膜两种功能，每个节点有6 个自由度。预应力钢筋选用Link8 三维杆单元，每个节点有三个平动自由度，通过赋予初应变施加结构预应力，赋予的初应变值是0．005。Solid45 用来模拟墩。模型建立采用圆柱坐标系，坐标原点位于桥梁轴线中心处，其中X 沿桥轴向，Y 沿圆弧的径向方向，以指向圆心为负，Z 为竖向，以向上为正。边界条件处理，在支座处根据实际情况施加竖向约束，墩底施加全部方向约束。具体约束情况见表2。主梁模型墩部梁截面、跨中截面如图1 所示，全桥模型如图2 所示。

2 恒载和预应力作用下结构内力计算与分析

因只对该类桥的内力做趋势分析，故该斜交弯梁桥的恒载仅包含了主梁自重; 预应力筋仅考虑了主

图1 梁截面图(单位:cm)

图2 全桥模型

要预应力的作用情况［10］。通过ANSYS 计算，结构自重和预应力引起的主拉应力如图3 所示，最大主拉、压应力随斜交角的变化如图4 所示，经计算得到斜交角从15°变化到60°，最大主拉应力增幅16．01%;最大主压应力增幅10．47%。

表2 模型束制情况

说明:表中“0”为释放，“1”为束制。

图3 最大主拉应力

为了便于对比分析，论文对提取的结果采用曲线图的方式进一步表述。见图4。

从曲线图4( c) 可看出支撑反力在边跨支撑处，内侧反力随斜交角度的增大而增大，而外侧反力则随之减小，这主要由于随着斜交角的增大，内力峰值向钝角方向靠拢，故斜交处内侧反力变大而外侧反力减小。斜交角对斜弯桥的影响是显着的，随斜交角的增加斜弯桥的受力增大。当斜交角度从15°增加到60°时，边跨支撑处内侧反力增加118．6%。内外侧支撑反力的差值也更是增加了240．5%。

从曲线图4( d) ，( e) 可看出在桥墩支撑处支反力都随斜交角度的增大而增大。并且支撑处外侧支反力明显大于内侧，验证了弯桥的支点反力有曲线外侧变大、内侧变小的倾向，即产生较大的扭转，通常会使外梁超载，内梁卸载，内外梁产生应力差别，使梁体有向外侧翻的趋势。这不仅与弯桥的曲线半径大小有关，还与斜交段的斜交角度有关。在边跨支撑处和P2墩顶左侧位置，随着斜交角度的增大，内外侧支反力的差值逐渐增大;而在P2墩顶右侧位置，由于支撑反力方向相反，随着斜交角度的增大，内外侧支反力的差值逐渐减小。

从图4( f) 可以看出扭矩的沿程分布的情况与斜交角的关系，随着斜交角的增大，各主要截面的扭矩明显增大。

图4 内力分析比较

3 计算结果与斜桥的力学特性的验证

通过对该斜交弯梁桥的计算分析，得出支撑反力在边跨支撑处，内侧反力随斜交角度的增大而增大，而外侧反力则随之减小，其他支撑反力都随斜交角度的增大而增大。为验证斜交弯梁桥关于斜交角力学特性的计算结果与理论是否一致，理论上对斜梁桥进行计算，判断其计算的合理性。

以单跨斜梁为例如图5，支座1 ～支座4 有反力为

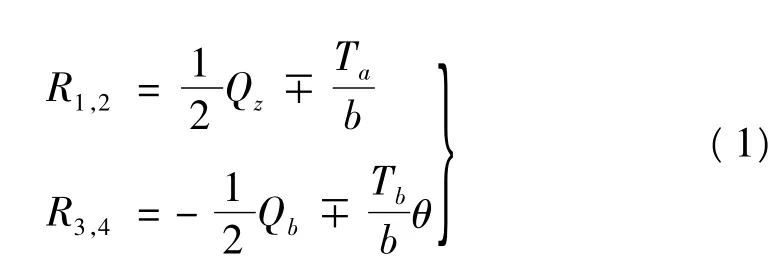
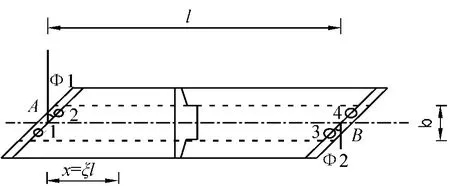
图5 单跨斜梁

式中，Qa，Qb为左右梁端剪力，数值上为各反力的代数和，即

Ta，Tb即为左右梁端R1与R2，R3与R4对梁轴的力矩，即

式中，k 为主梁弯扭刚度比，k = EI/GJ; EI 为抗弯刚度; GJ 为抗扭刚度; l 为计算跨径; ξ 为集中荷载P作用的相对位置。

进而有

式中，x = ξl; b 为支座间距。

由式(4) 可知，钝角反力R2，R3大于锐角反力R1，R4，即R2比R1大比R4大，R3比R4。二者的反力差与斜度φ 及弯扭刚度比k 有关。很明显，斜度越大，二者的反力差越大;弯扭刚度比越小( 即抗扭刚度越大) ，二者反力差越大。即在钝角反力增大的同时，锐角的反力在减小，甚至可能出现负反力。

反力的这一特性在板桥及多梁式桥中均是如此，具体表现在多个支座时，各支座的反力分布不均，钝角区域的反力比锐角区域的反力大。

4 结语

(1) 验证分析了斜交桥随着斜交角的增大，内力峰值向钝角方向靠拢，故斜交处内侧反力变大而外侧反力减小。

(2) 通过计算结果与理论分析比较，验证了板单元理论的有效性和准确性，同时也说明了空间板单元有限元分析方法把异型复杂的结构模拟成一个纵、横交叉的空间体系，体系力学模型符合结构的实际受力情况，可以直接得到结构的内力与变形，是一种简便实用的分析方法。可供设计和施工人员参考和借鉴。

［1］邵容光，夏淦．混凝土弯梁桥［M］．北京:人民交通出版社，1996．

［2］姚玲森．曲线梁［M］．北京:人民交通出版社，1989．

［3］项海帆．高等桥梁结构理论［M］．北京:人民交通出版社，2001．

［4］吴西伦．弯梁桥设计［M］．北京:人民交通出版社，1990．

［5］贺拴海．桥梁结构理论与计算方法［M］．北京:人民交通出版社，2003．

［6］陈俊真．南昆铁路板其2 号大桥——我国铁路第一座平弯梁桥［J］．铁道标准设计，1999(5) :9-14．

［7］孙学先，张慧．反演理论在悬臂灌筑平弯梁桥线形监控中的应用［J］．工程力学，2007(12) :135-139．

［8］程永华，张彧．曲线半径变化对斜交弯梁桥结构变形的计算分析［J］．城市道桥与防洪，2007(2) :30-32．

［9］杨明，黄侨，王德军．Equivalent bending stiffness of simply supported preflex beam bridge with variable cross-section［J］．哈尔滨工业大学学报:英文版，2010(1) :13-17．

［10］陈黎明，张运波，王海良．对连续弯梁桥空间转角近似计算方法的探讨［J］．石家庄铁道学院学报，2003，16( S1) :56-58．