铁路无缝线路钢轨温度力测定理论分析

梁素平， 李向国

( 石家庄铁道大学 土木工程学院，河北 石家庄 050043)

为了适应铁路运输重载、高速发展的需要，轨道结构随之发生了较大变化，当几十根甚至几百根标准钢轨焊接在一起时，就变为了无缝线路乃至超长无缝线路。随着我国无缝线路的发展，无缝线路已广泛应用于铁路轨道。无缝线路轨道消除了钢轨接头，使列车运行平稳，减少轨道与机车车辆损伤，维修费用低，使用寿命长，能提高列车舒适度，降低轮轨振动与噪声，已被接受并广泛应用。但由于无缝线路中钢轨不能自由伸缩，当环境温度发生变化时钢轨温度也随之变化，于是在钢轨内部产生很大的轴向温度力。如果不能及时、准确地掌握无缝线路钢轨温度力状况，并对钢轨的温度力超限地段及时调整、放散，就可能发生胀轨跑道和断轨的危险，危机行车安全［1-2］。因此研究具有初始弯曲的钢轨内轴向温度力与轨道各参数的关系以及轨道各参数对温度力测定值的影响是无缝线路研究中的关键课题。

1 温度力计算式推导

1．1 横向位移法介绍

横向位移法测试钢轨温度力［3-4］，是将测试段钢轨中间扣件拆除并在钢轨松开后撤去钢轨下的胶垫，两端扣件将钢轨固定，使钢轨两端约束中间自由。标定被测试段钢轨长度，在此标定段中间钢轨曲率中心一侧施加一水平作用力，并在施加水平力处的钢轨另一侧测量钢轨横向位移，同时测量标定段钢轨此时的温度。然后将所施加的力、标定长度、曲率半径、所测得的钢轨横向位移以及不同类型钢轨的刚度EI代入公式，即可求得钢轨温度力。根据无缝线路温度力计算公式N = EFαΔT，可求得钢轨温度变化ΔT，从而将所测钢轨温度代入ΔT = Tg- Ts，求得锁定轨温。其中，Tg为所测得的钢轨的温度，Ts为锁定轨温。

1．2 计算式推导

假设一具有初始弯曲的钢轨是一无限连续体，从中截取一段为研究对象，解除轨枕对其约束，其力学计算模型见图1。

图1 中N 为钢轨内存在的温度力; P 为钢轨跨中上施加的侧向荷载; u 为钢轨产生的径向位移; Fy为钢轨跨端部施加的侧向力;弯矩为M0。

设钢轨抗弯刚度为EI，支座抗弯刚度H，曲线切线与X 轴的夹角为φ，圆弧拱的弦切角为θ，其中L为所取钢轨总长，R 为轨道曲率半径。

图1 轨道力学计算模型

由平衡条件得Fy= p/2 - Nsin θ，各截面弯矩为

曲线径向位移微分方程［5］为

由式(1) 、式(2) 可得

由于实际中θ 很小，所以φ 很小，此处令cos φ = cos θ，并由a = ( NR2cos2θ) /EI -1 ，式(3) 变为

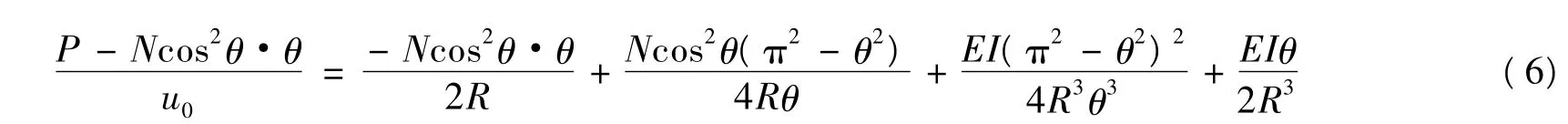
通过式(6) 计算出N 后，即可根据N = EFαΔt 求出锁定轨温与实际轨温之差Δt。

2 各参数对温度力的影响分析

2．1 温度力的影响参数

温度力是影响轨道稳定性的一个重要因素，尤其是重载铁路。75 kg/m 钢轨横断面面积F 为95．073 cm2，钢轨对竖直轴的惯性矩Jy= 665 cm4，线膨胀系数α = 11．8 ×10-6℃，其余参数的基准值及变化范围见表1。

表1 各参数的基准值及变化范围

2．2 温度力的影响分析

根据理论推导的钢轨温度力的计算式，求解出不同钢轨跨中横向位移、轨道曲线半径、钢轨长度、钢轨弹模以及钢轨磨耗下的温度力，并绘制它们的关系曲面图。曲线半径、钢轨长度、钢轨弹模、钢轨磨耗与横向位移以及温度力之间的关系如曲面图2 ～图5 所示( 绘制任意三者的曲面图均假定其他值为基准值) 。从图2 ～图5 中可以看出:

图2 曲线半径、横向位移及温度力三维面图

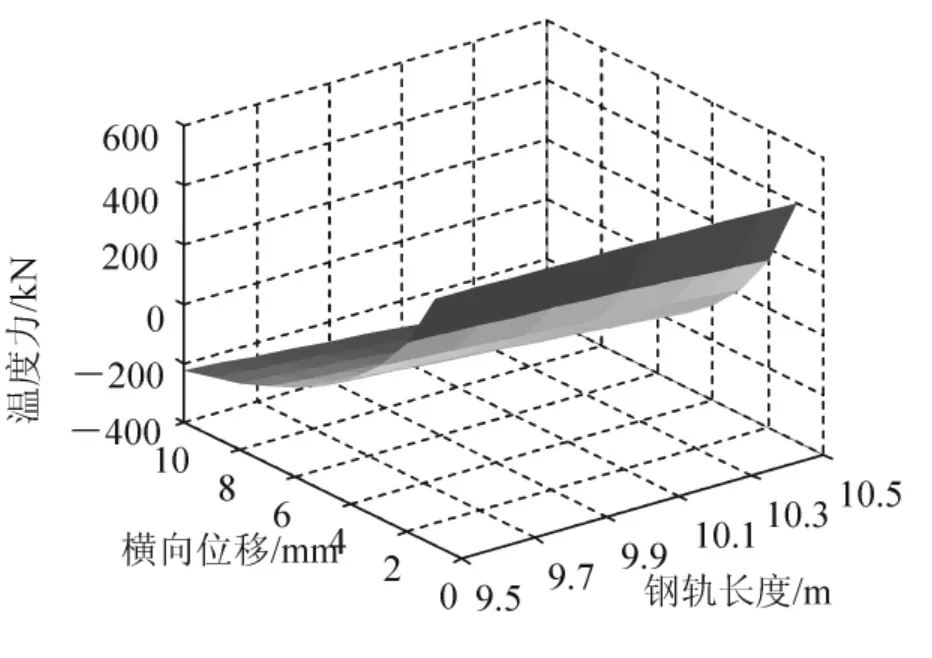
图3 钢轨长度、横向位移及温度力三维面图

图4 钢轨弹模、横向位移及温度力三维面图

图5 钢轨磨耗、横向位移及温度力的三维面图

(1) 钢轨跨中横向位移和轨道曲线半径对钢轨温度力测定值的影响是非线性的;钢轨长度、钢轨弹性模量以及钢轨磨耗对钢轨温度力测定值的影响是线性的。

(2) 轨道曲线半径从300 m 变化到14 000 m 时，曲线半径越小对钢轨温度力测定值的影响越大;曲线半径越大对钢轨温度力测定值的影响越小。即钢轨温度力测定值随曲线半径的变化斜率随着曲线半径的增大而减小。且钢轨跨中横向位移在4 mm 附近时，曲线半径变化对钢轨温度力测定值的影响较小。

(3) 钢轨长度在9．5 ～10．5 m 之间变化时，钢轨长度增大，测定的钢轨温度拉力、压力均增大。且横向位移越大，钢轨长度变化对温度力测定值的影响越大。

(4) 钢轨弹模在201 ～210 GPa 之间变化时，钢轨温度力测定值的变化较小。即钢轨弹模对钢轨温度力测定值的影响较小。随着横向位移的增大，钢轨弹模对钢轨温度力测定值的影响增大，但增大的很慢。

(5) 钢轨磨耗较小时，对钢轨温度力测定值的影响较小。相同横向位移时，随着磨耗的增大，测定的钢轨温度拉力增大、压力减小。且钢轨磨耗对钢轨温度力测定值的影响随着横向位移的增大而增大，但增大的速度较小。

3 结论

通过钢轨温度力计算式的推导以及各参数对温度力测定值的影响分析，可知横向位移与轨道曲线半径对钢轨温度力测定值的影响时非线性的;钢轨长度、钢轨弹模、钢轨磨耗对钢轨温度力测定值的影响是线性的。各参数对钢轨温度力测定值的影响大小均与钢轨跨中横向位移有关，三者对钢轨温度力测定值的影响均随着横向位移的增大而增大。通过比较得出，曲线半径、钢轨长度对钢轨温度力测定值的影响较大;钢轨弹模、钢轨磨耗对温度力测定值的影响较小。

［1］李向国．高速铁路技术［M］．北京:中国铁道出版社，2008．

［2］练松良．轨道工程［M］．上海:同济大学出版社，2006．

［3］刘永前，王建文，邹振祝．无缝线路钢轨温度力测试的位移法［J］．铁道学报，2005，27(4) :125-128．

［4］王建文．无缝线路钢轨温度力及锁定轨温的测试方法:中国，02104896．7［P］．2004-12-22．

［5］朱宏光．传统弯桥微分方程求解中一个理论问题［J］．中国铁道科学，2006，27(4) :18-21．