对称层合折板结构自由振动分析的移动最小二乘无网格法

彭林欣

(广西大学 土木建筑工程学院，南宁 530004)

由于有着高刚度—重量比、易成型、低成本的优点，折板结构被广泛应用于各类实际工程，如屋盖、夹层板核、船体以及冷却塔等等。在纤维增强复合材料发明之前，折板一般由金属或木材制成。层合折板的出现，有机地结合了纤维增强复合材料和折板结构的优点，使整个结构更轻刚性更好。

各向同性折板的研究已有很长的历史，方法多种多样。由于缺乏分析工具，早期的学者只能通过不同程度的近似来研究这种结构，发展了梁模型和忽略折板接合处相对位移的模型［1］。由于过多的简化，这些模型分析一般折板结构的效果并不理想。Gaafar［2］，Yitzhaki［3］和 Whitney 等［4］最先在他们的方法中考虑了接合处相对位移，为更精确求解折板问题铺平道路。国内方面，赖远明等［5］对简支V形折板屋盖进行了研究;刘金堂等［6］采用微分求积法分析了轴向运动薄板的横向振动。随着计算机技术的发展，数值方法逐渐在结构分析中扮演重要角色，有限条法［7，8］和有限元法［9，10］纷纷被引入求解各向同性折板问题。

尽管被广泛使用，层合折板相关的分析研究却不多，目前只有 Guha-Niyogi等［11］和 Lee 等［12］在结构振动方面用有限元法开展的工作以及郑荣跃等［13］给出的箱型正交异性矩形板结构自由振动问题解析解。

综合来看，不论是各向同性折板、层合折板还是其他结构，有限元法均是占主流地位的分析工具。这是由有限元法适应性好、精度高等优点决定的。但基于网格构建近似解的有限元法也有弱点——当网格扭曲发生，只能对问题域进行网格重构——不但增加了分析的复杂程度，计算精度也受到了影响。作为有限元法之外的另一选择，无网格法［14-17］近年来引起了越来越多的关注。无网格法将问题的近似解完全建立在问题域中相互无直接联系的离散节点上，更灵活，适应性也更强。

本文将利用无网格的优势，提出一种求解对称层合折板结构自由振动问题的移动最小二乘无网格法。基于作者提出的折板无网格模型［17］，先按一阶剪切变形理论［18］和移动最小二乘近似［14］得到各对称层合平板的刚度和质量矩阵，再将它们分别叠加得到整个结构的刚度和质量矩阵。文末用本文方法求解了几个数值算例，并与有限元软件ANSYS分析结果进行了对比。本文方法也可用于分析箱梁和封闭结构。

1 移动最小二乘近似

设某个定义于域Ω上的函数v(x)可以被函数vh(x)在子域Ωx上近似，

其中，qi(x)是已知的多项式基函数，m是基函数个数，bi(x)是相应的未知系数。本文使用二次基:

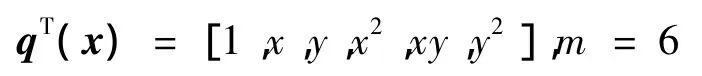
未知系数bi(x)可以通过使一个L2模:

由式(3)得到:

将式(4)代入式(1)，可以将vh(x)表示为标准形式:

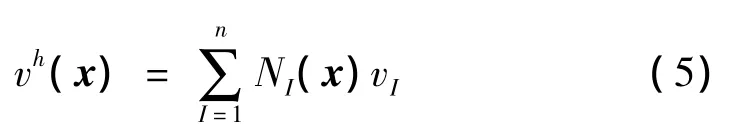
其中形函数:

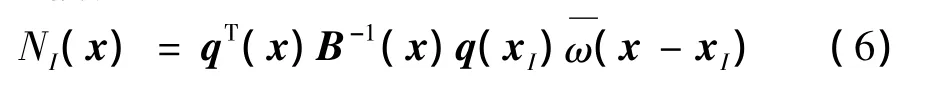
2 层合平板列式

按照作者针对各向同性折板提出的无网格模型［17］，首先应推导出对称层合平板的刚度和质量矩阵。如图1，局部坐标系下的对称层合平板无网格模型，包括分布于板中面的一系列离散节点。节点的自由度是(u0，v0，w，φx，φy)，其中，u0，v0，w表示板节点沿x、y、z方向的平动，φx，φy表示绕y轴和x轴的转角。设板共有N层，每层高度为zi(i=1，…，N)，第k层厚度为hk=zk+1-zk。

图1 层合板无网格模型Fig.1 Meshfree model of a laminate

2.1 近似位移场

按一阶剪切变形理论［18］和移动最小二乘近似［14］，层合板的位移场为:

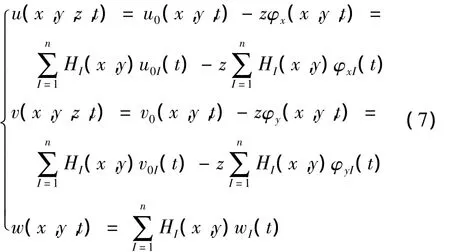
其中，{u0I(t)，v0I(t)，wI(t)，φxI(t)，φyI(t)}T= δI是板上第I个节点的节点参数，为时间t的函数。n是板的节点个数。形函数HI(x，y)由式(6)，选用三次样条函数:

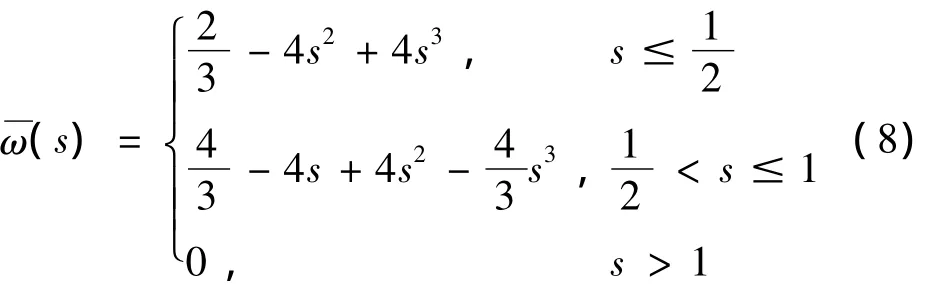
作为权函数计算得到。式(7)可写成矩阵形式:

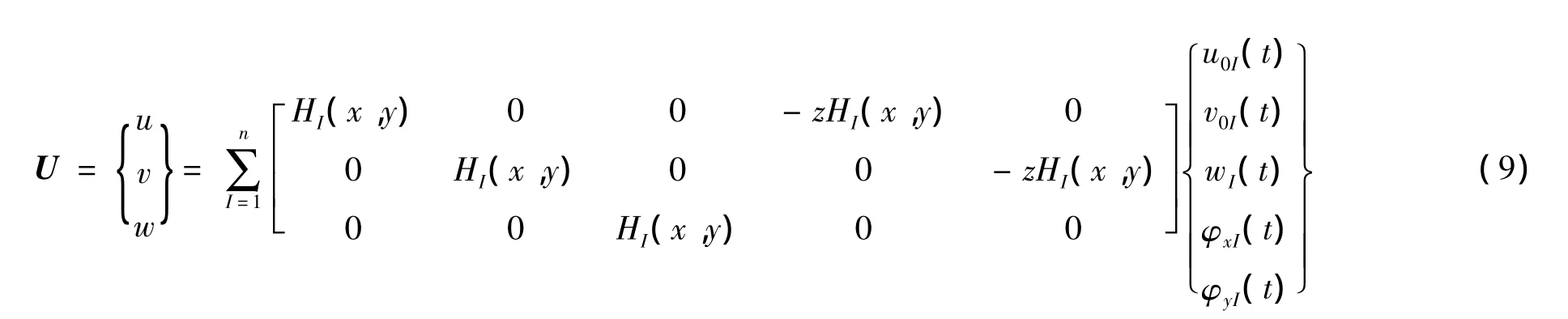
板的应变为:

这里，

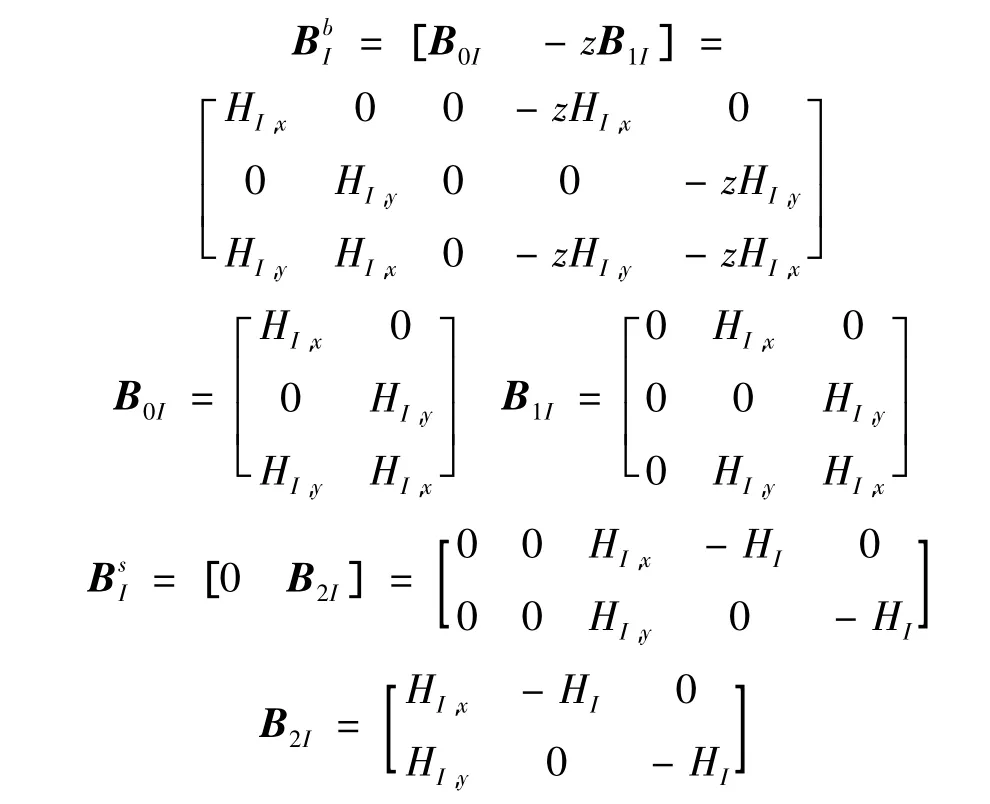
2.2 控制方程

自由振动时，层合平板的变形能和动能分别为:

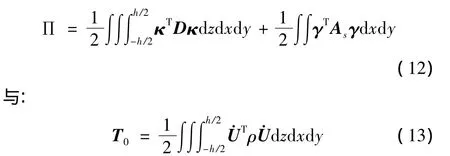
其中:

(i，j=1，2，6，4，5)是文献［18］中定义的板第k层材料刚度，在层内为常数，kc=5/6为剪切修正系数，h为板厚，ρ为材料密度。

由Hamilton原理:

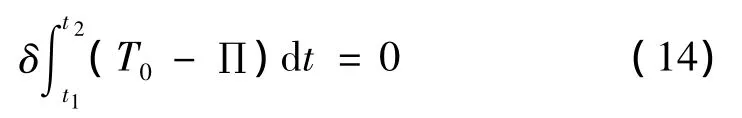
将式(9)～式(13)代入式(14)得:

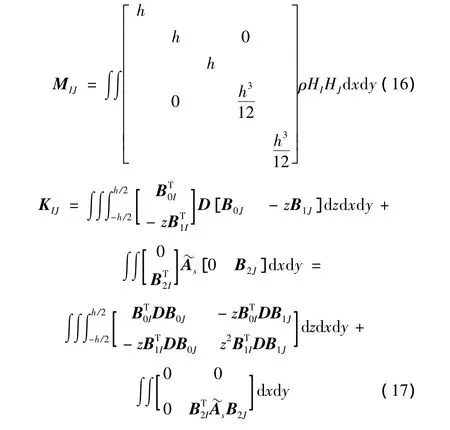
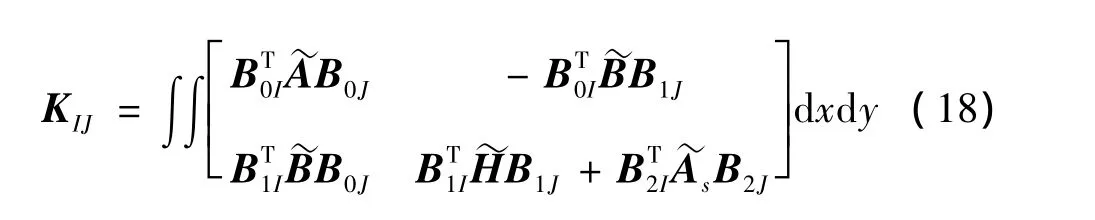
3 层合折板列式

根据折板的无网格模型［17］，在推导出层合平板自由振动的控制方程，得到相关刚度和质量矩阵后，下一步是将它们叠加起来，得到整个折板的刚度和质量矩阵。为了达到这个目的，将每个平板视为一个大单元(图2)，通过两单元连接处的重合节点具有相同真实位移的协调条件，将它们刚度和质量矩阵叠加。

然而，正如作者在文献［17］中指出的，由于从式(6)得到的形函数不满足克罗内克条件，式(15)中δ是节点参数而非节点真实位移，所以各平板的刚度和质量矩阵不能直接叠加。这里还将像文献［17］一样的处理，先基于全转换法(Full transformation method)［15］推导适用于平板分析的修正矩阵，再用该矩阵对平板刚度和质量矩阵进行修正，然后将它们叠加得到整个结构的刚度和质量矩阵，最后再施加本质边界条件。全转换法是Chen等学者提出，最初仅用于处理无网格计算中的本质边界条件施加问题。作者将此方法引入了复合结构的无网格建模中，得到了较好的分析结果。

图2 层合折板无网格模型——包括两个大单元(层合平板)，节点i的影响域以虚线显示Fig.2 A meshfree model of a folded laminated plate that is made up of two big elements

3.1 刚度和质量矩阵的修正

考虑到近似位移:

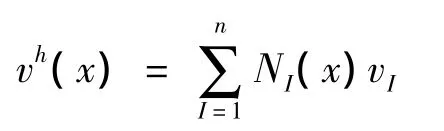
则真实节点位移:

其中:

对于本文的层合平板问题，相应的有:

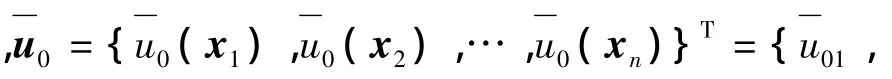
式(20)可综合成:

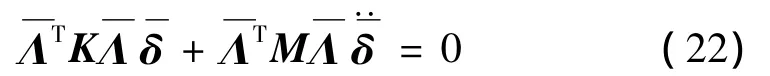
3.2 层合折板控制方程

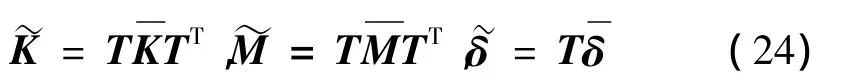
其中T是文献［17］中使用的6n×6n坐标变换矩阵(注意:此时中将增加节点转动自由度φz，即和也要做相应的扩充，增加的均为零元素)。然后可通过引入位移协调条件，将各层合平板在整体坐标系下的修正刚度、质量矩阵叠加。以图2中两个大单元(层合平板)组成的折板为例，设在两平板交界线上有编号1～J共J个重合节点，两平板在这些节点上应有相同的真实节点位移，即有:

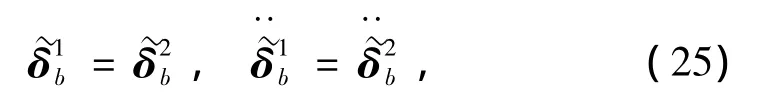
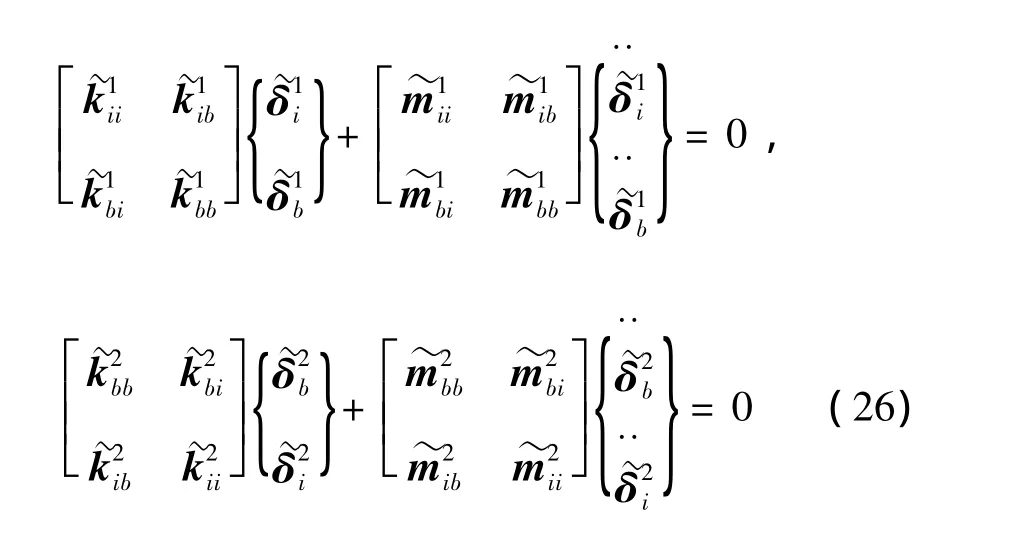
即为整个结构的自由振动控制方程:

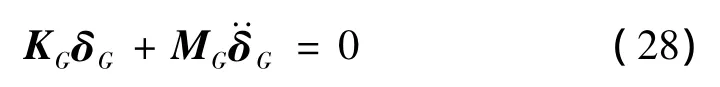
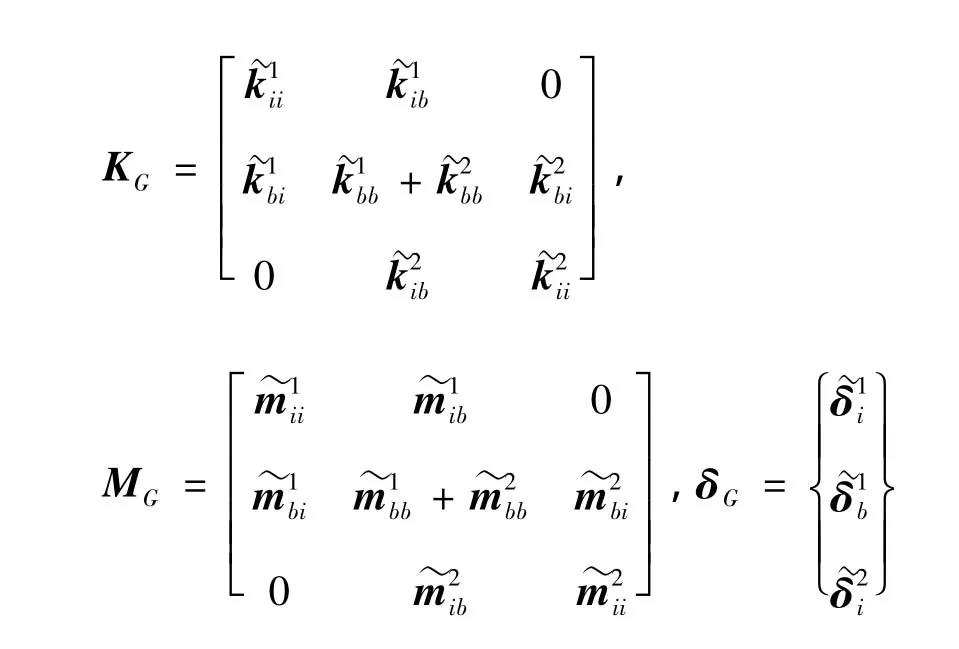
其中:

求解对应的特征值问题

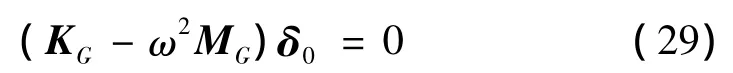
即可得该层合折板自由振动的频率。由于式(24)中增加了节点转动自由度φz和做相应扩充后在主对角线上会出现零元素，这可导致式(29)中的KG和MG主对角线上某元素为零，产生奇异性。本文采取以下办法解决这个问题:将KG主对角线上零元素所在行、列的全部元素从KG中划去，MG对应的行、列全部元素以及δ0对应的行上元素也划去。

4 算例

以下算例中，层合平板的材料参数均设为:

E1=2.5 × 107Pa，E2=1 ×106Pa，G12=G13=5 ×105Pa，G23=2 ×105Pa，μ12=0.25，或以式(12)中使用的材料刚度表示为:

(1)纤维铺设角θ=0°时，

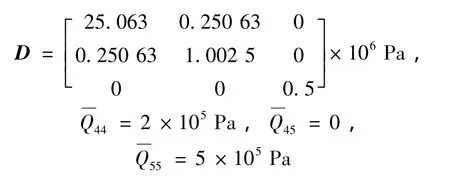
(2)θ=90°时，

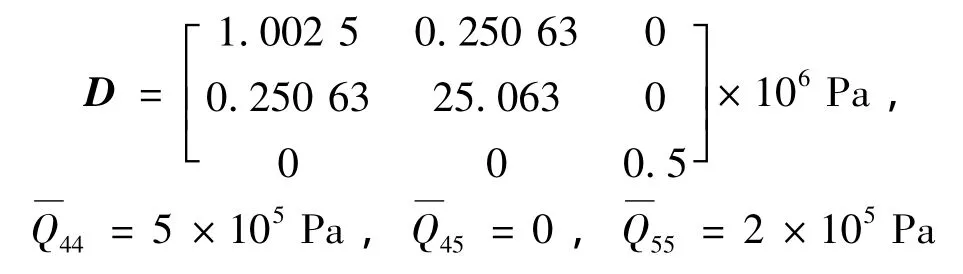
(3)θ=45°时，

(4)θ=-45°时，

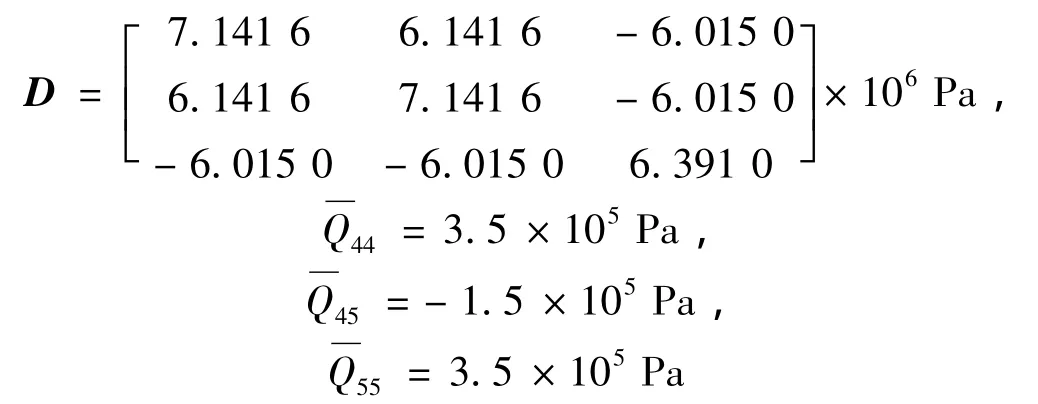
4.1 单折层合折板

一单折层合折板，由两相同层合方平板组成，α=120°，一边固支(图3)，层合方板纤维铺设角度和铺层顺序为(-45°/45°/45°/-45°)。经有限元分析和本文方法计算得到的该结构前五阶自由振动频率列在表1中。其中，本文无网格解基于以下离散方案:各平板，11×11均布节点，方形影响域:

hx为影响域X向长度，hy为Y向长度，Ix为X向相邻两节点间距，Iy为Y向相邻两节点间距，取系数β=4;有限元解通过ANSYS软件，将该层合折板模拟为层合壳结构，选用SHELL99单元进行离散后计算得到，单元数:3 200。由表1可见，本文解与有限元解吻合良好。计算效率方面，本文方法与ANSYS求解时间之比为1.1∶1，说明有限元法效率更高。

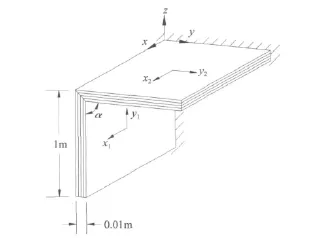
图3 一边固支单折层合折板Fig.3.A one-fold laminated plate with one side fixed

4.2 三面层合壳结构

如图4，用三个尺寸相同的层合方平板组成一个三面层合壳结构(即从一正方盒子中取一半)，板 厚 为 0.01 m，在三个角点 A、B、C上用球铰约束——使该点只能转动不能平动。当各平板取不同的纤维铺设角度和铺层顺序时(图5)，由本文方法和有限元分析给出的该结构前五阶自由振动频率列在表2～4中。本文解基于与4.1相同的离散方案;有限元解由ANSYS软件采用SHELL99单元离散该层合壳结构得到，共有4 800个单元。从表2～表4可见，两者依然非常接近。

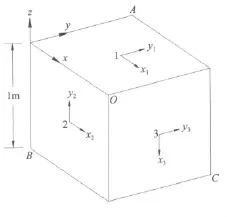
图4 三面层合壳结构Fig.4 A laminated shell structure

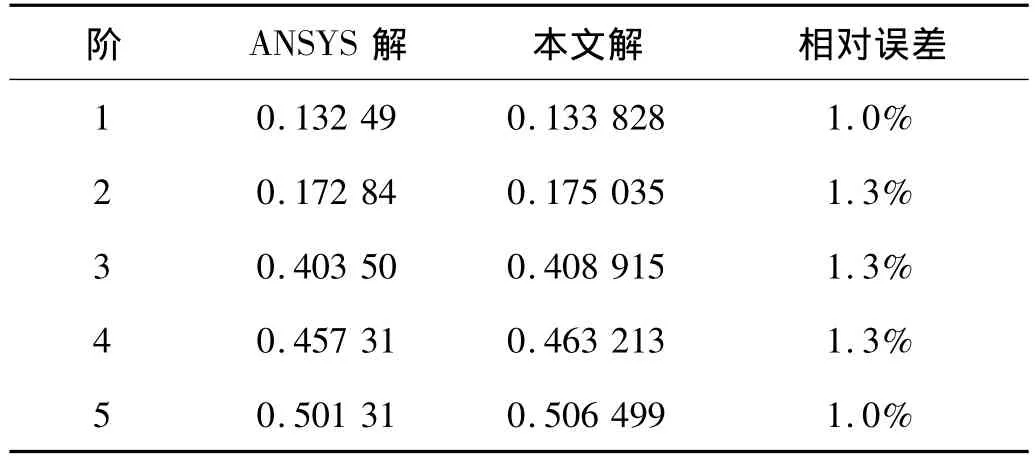
表1 单折层合折板自由振动频率(Hz)Tab.1 Free vibration frequencies(Hz)of the one－fold laminated plate

表2 三面层合壳结构(图5a)的自由振动频率(Hz)Tab.2 Free vibration frequencies(Hz)of the laminated shell(Fig.5 a)

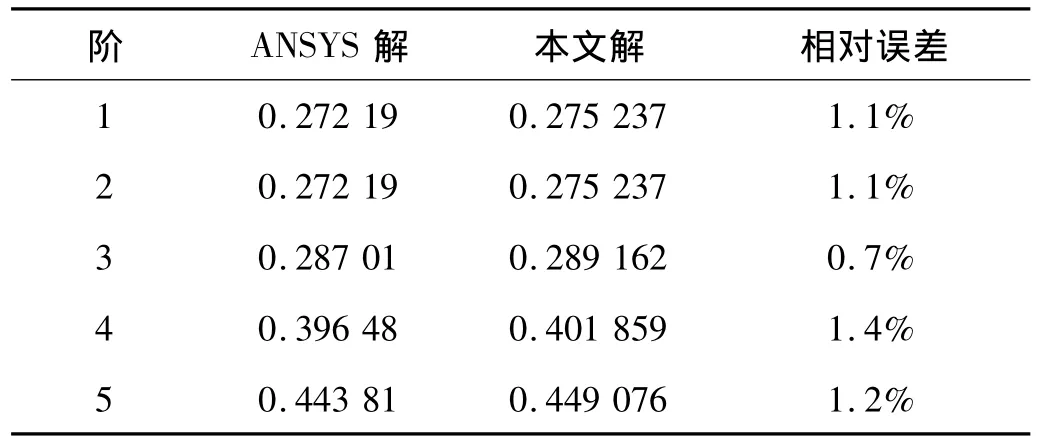
表3 三面层合壳结构(图5b)的自由振动频率(Hz)Tab.3 Free vibration frequencies(Hz)of the laminated shell(Fig.5 b)

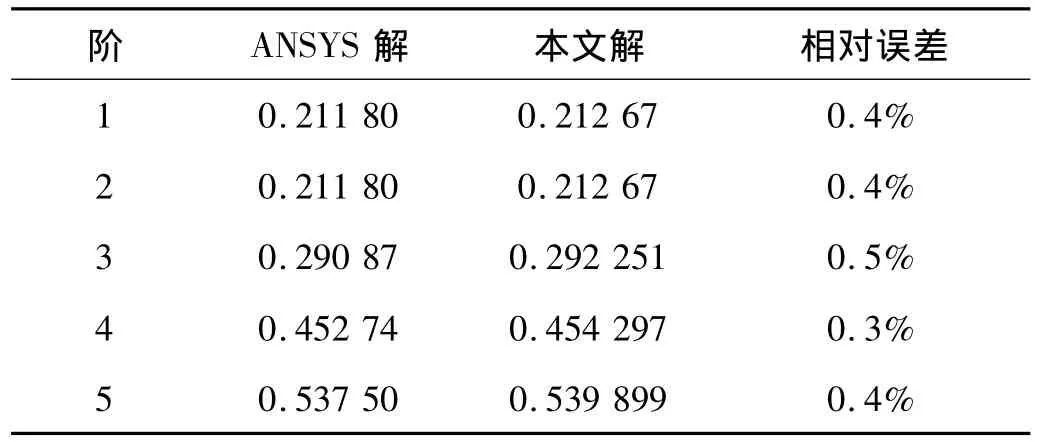
表4 三面层合壳结构(图5c)的自由振动频率(Hz)Tab.4 Free vibration frequencies(Hz)of the laminated shell(Fig.5 c)

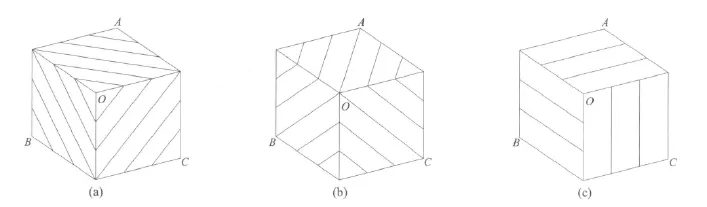
图5 三面层合壳结构的纤维铺设模式Fig.5 Lamination schemes of the laminated shell

图5中，(a)表示平板2和3的纤维铺设角度和铺层顺序为(-45°/45°/45°/-45°)，板1 为(45°/-45°/-45°/45°);(b)表示板 2 和 3 为(45°/-45°/-45°/45°)，板1 为(-45°/45°/45°/-45°);(c)表示板 2 和3 为(0°/90°/90°/0°)，板1 为(90°/0°/0°/90°)。

5 结论

本文提出一种求解对称层合折板结构自由振动问题的移动最小二乘无网格法。将层合折板结构视为由不同平面上对称层合板组成的复合结构，先基于一阶剪切变形理论和移动最小二乘近似得到各平面上层合平板的刚度和质量矩阵，经全转换法修正后叠加得到整个折板的刚度和质量矩阵，建立描述层合折板结构自由振动行为的控制方程。文末算例表明，本文方法解与有限元分析结果接近，验证了方法的准确性。本文方法也可用于分析箱梁和封闭结构。

［1］Task Group of the Subcommittee on Masonry and Reinforced Concrete of the Structural Division.Phase I report on folded plate construction ［J］.Journal of Structural Division，ASCE，1963，89:365-406.

［2］Gaafar I.Hipped plate analysis considering joint displacement［J］.Trans ASCE，1954，119:743-784.

［3］Yitzhaki D.Prismatic and cylindrical shell roofs［M］.Haifa，Israel，Haifa Science，1958.

［4］Whitney C S，Anderson B G，Birnbaum H.Reinforced concrete folded plate construction［J］.Journal of Structural Division，ASCE，1959，85:15-43.

［5］赖远明，王起才，孙爱良.简支交叉V形折板屋盖的内力和挠度［J］.计算力学学报，1997，14(4):477-483.

［6］刘金堂，杨晓东，闻邦椿.基于微分求积法的轴向运动板横向振动分析［J］.振动与冲击，2009，28(3):178-181.

［7］Cheung Y K.Folded plate structures by finite strip method［J］.Journal of Structural Division，ASCE，1969，95:2963-2979.

［8］Golley B W，Grice W A.Prismatic folded plate analysis using finite strip-element［J］.Computer Methods in Applied Mechanics and Engineering，1989，76:101-118.

［9］Liu W H，Huang C C.Vibration analysis of folded plates［J］.Journal of Sound and Vibration，1992，157(1):123-137.

［10］Perry B，Bar-Yoseph P，Rosenhouse G.Rectangular hybrid shell element for analysing folded plate structures ［J］.Computers＆ Structures，1992，44(1-2):177-185.

［11］ Guha-Niyogi A，Laha M K，Sinha P K.Finite element vibration analysis oflaminated composite folded plate structures［J］.Shock and Vibration，1999，6:273-283.

［12］Lee S Y，Wooh S C，Yhim S S.Dynamic behavior of folded composite plates analyzed by the third order plate theory［J］.International Journal of Solids and Structures，2004，41:1879 1892.

［13］郑荣跃，黄 炎，蔺文峰.箱形正交异性矩形板结构的自由振动分析［J］.振动与冲击，2009，28(3):161-163，167.

［14］ Belytschko T，Lu Y Y，Gu L.Element-free Galerkin methods［J］. InternationalJournalforNumericalMethods in Engineering，1994，37:229-256.

［15］ Chen J S，Pan C，Wu C T，et al.Reproducing kernel particle methods for large deformation analysis of nonlinear structures［J］.Computer Methods in Applied Mechanics and Engineering，1996，139:195-227.

［16］周小平，周瑞忠.无单元法研究现状及展望［J］.工程力学，2005，22(1):12-20.

［17］Peng L X，Kitipornchai S，Liew K M.Bending analysis of folded plates by the FSDT meshless method［J］.Thin-Walled Structures，2006，44(11):1138-1160.

［18］ Reddy J N，Miravete A.Practical analysis of composite laminates［M］.Boca Raton，USA，CRC Press，1995.