非线性弹簧支承悬臂输液管道的分岔与混沌分析

唐 冶，方 勃，张业伟，李庆芬

(1.哈尔滨工业大学 航天学院，哈尔滨 150001;2.哈尔滨工程大学 机电工程学院，哈尔滨 150001)

输液管道的振动问题不仅有较高的理论研究基础，而且还有广阔的工程应用背景。输液管道的非线性动力学行为作为振动的前沿问题，很多学者对此作了较为深入的研究，他们根据输液管道系统存在的大量非线性现象，采用不同分析方法，得到了很多此系统的运动规律。Holmes［1］利用Lyapunov直接法研究了两端固支的输液管道在自激作用下全局动态行为，研究结果表明其运动轨线不存在极限环，即该类管道的稳态运动不会发生颤振。Paidoussis等［2，3］人研究了带非线性弹簧运动约束悬臂输液管道的非线性动力学行为，他们得到了输液管道系统通过倍周期分岔转变为混沌运动的规律。Tang和Dowell［4］通过对输液管道施加强非线性力来研究其混沌特性，得到了使系统出现混沌的力临界值与流速密切相关。金基铎［5］用理论分析的方法详细研究了受约束悬臂输液管道系统可能发生的复杂运动和运动分岔现象，在动态失稳区域内存在管道的概周期运动和由于概周期运动环面破裂而导致混沌的现象。倪樵［6］运用微分求积法研究了在谐激励作用下输流曲管的混沌振动，结果表明在不同流速和激励频率的参数区域内，系统将可能发生包括混沌振动在内的多种运动形式。包日东［7］采用非线性动力学分析方法，研究两端一般支承输流管道系统在自激、参数激励和外激励联合作用下的非线性动力学特性。

本文研究了左端具有非线性弹簧支承和中间悬臂的输液管道系统的非线性动力学行为。在文献［8］基础上，建立了非线性弹簧支承悬臂输液管道的运动微分方程，以在线性弹簧支承条件下悬臂梁的固有频率和振型函数作为近似，利用李兹-伽辽金方法对此方程在模态空间内展开，得到关于时间的二阶常微分方程组，引入状态变量将其改写成一阶状态方程组。再应用分岔图、相图和功率谱图研究非线性振动的数值仿真方法，研究该类管道系统在自激励、参数激励和外激励联合激励下的振动响应问题，重点揭示系统在流体的平均流速和流体与管道质量比变化时可能出现的运动形态以及对应的参数条件，为今后分析和研究非线性弹簧支承悬臂输液管道的动态响应和振动控制提供理论依据。

1 输液管道系统的运动微分方程

图1 非线性弹簧支承悬臂输液管道的理论模型Fig.1 The theoretical model of cantilever pipeline conveying fluid with nonlinear spring support

如图1所示长度为l的非线性弹簧支承悬臂输液管道，左端是非线性弹簧支承，中间是固定支承，流体从左端流入右端流出，考虑Kelvin-Voigt粘弹性管材、管内流体压力效应和管截面的轴向作用，由达朗伯原理和牛顿力学原理，此系统的运动微分方程［9，10］:

式中，y为管道轴线偏离平衡位置的位移，x为管道横截面处的位置，EI为管道的抗弯刚度，a为管材粘弹性系数，M为单位长度流体的质量，m为单位长度管道的质量，U为管道内流体的流速，P为流体的压强，t为时间，l为管道长度，A为管道的横截面积，g为重力加速度。

输液管道左端所受非线性弹簧支承约束对管道的反作用力可表示:

式中δ()表示Dirac delta函数，K1与K2分别是弹簧的线性和非线性的刚度系数。

在工程实际中，与输液管道系统相连接的支承基础在某种外力的作用必然会引起自身的振动，这种振动必定会作用于管道系统。所以对管道系统施加一个运动方向垂直于管道轴线的简谐运动:

式中，D为激励振幅，w为激励频率。

考虑式(2)和式(3)，得到修正后的非线性弹簧支承悬臂输液管道系统运动微分方程:

引入下列无量纲参数:

将上面各式代入方程(4)中，得到无量纲化的非线性弹簧支承悬臂输液管道系统运动微分方程:

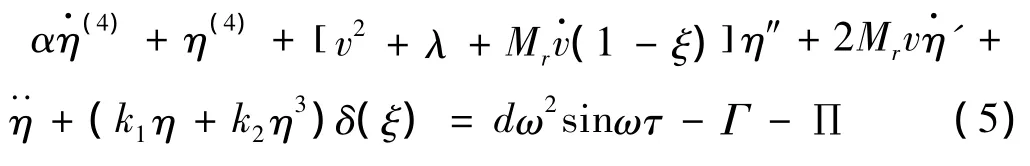
设无量纲化的脉动流速表达形式:

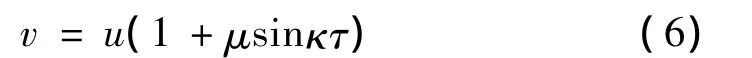
式中，u为流体平均流速，μ为流速脉动幅值，κ为流速脉动频率。

设无量纲化的脉动压强表达形式:

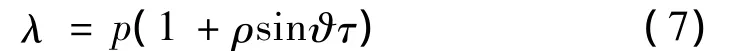
式中，p为流体平均压强，ρ为压强脉动幅值，ϑ为压强脉动频率。

将式(6)和式(7)代入式(5)，可得到无量纲化的非线性弹簧支承悬臂输液管道系统在脉动流速、脉动压强和基础简谐运动(自激励、参数激励和外激励)联合激励下的运动微分方程:

2 梁系统的频率方程和振型函数

本文是以在线性弹簧支承条件下悬臂梁的固有频率和振型函数作为输液管道系统的近似固有频率和振型函数，因此如图2所示设xj(j=1，2)表示梁横截面位置坐标，其中0＜x1＜xb，0 ＜x2＜l-xb，Xj(xj)(j=1，2)表示相应位置坐标处梁横向变形位移。线性弹簧支承悬臂梁系统的振型函数［8］:

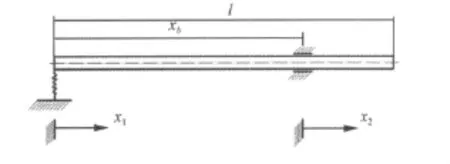
图2 线性弹簧支承悬臂梁的理论模型Fig.2 The theoretical model of cantilever beam with linear spring support

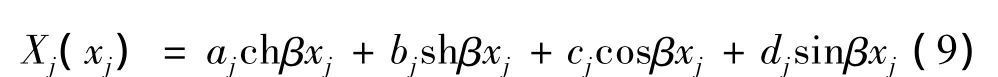
式中，β 为系统的特征值，aj，bj，cj，dj(j=1，2)为积分常数。

线性弹簧支承悬臂梁系统的边界条件［8］:

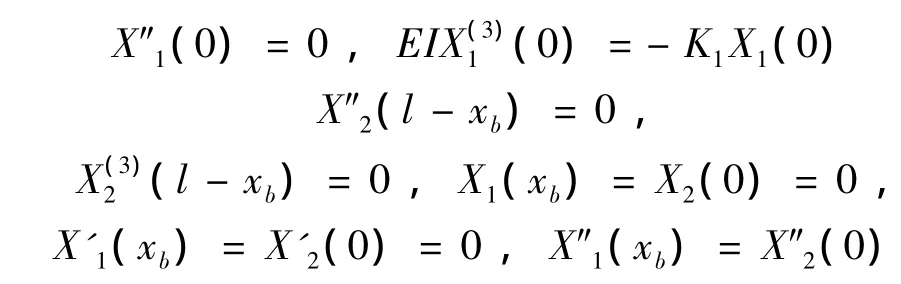
将边界条件分别代入式(9)中，有方程组:

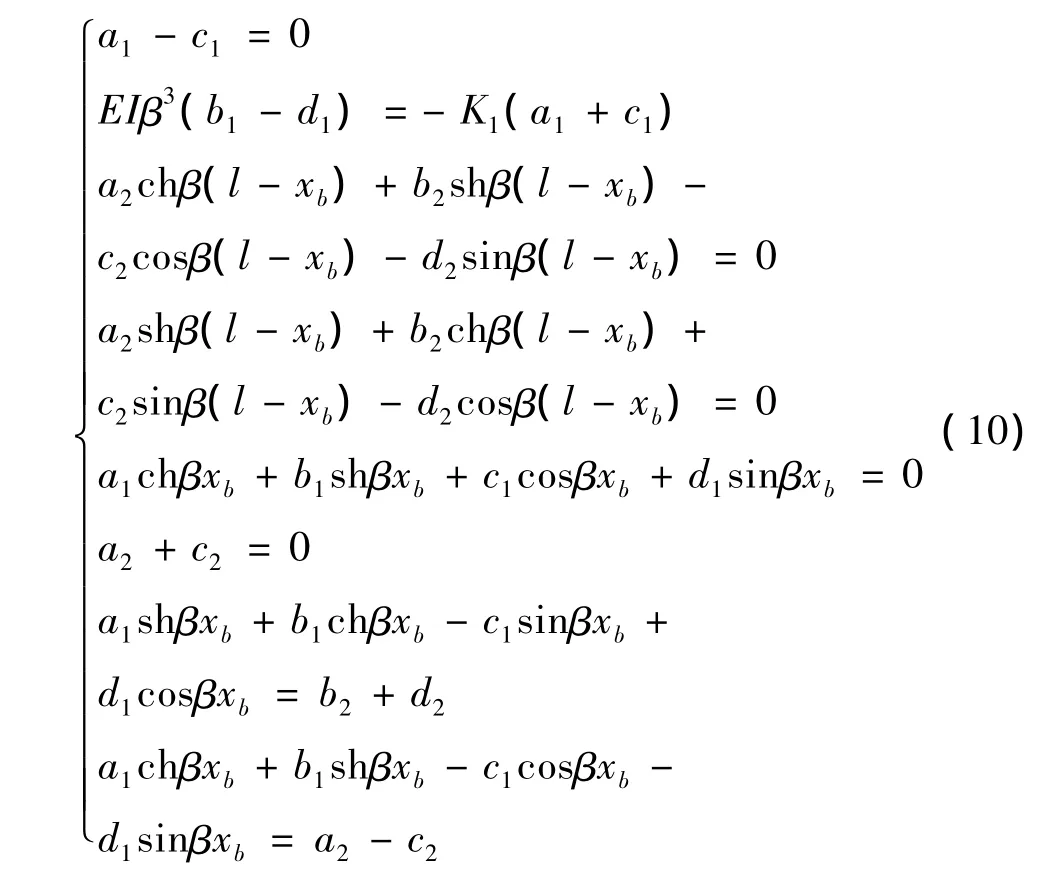
由积分常数aj，bj，cj，dj(j=1，2)有非零解，经无量纲处理得线性弹簧支承悬臂梁系统的频率方程［8］:

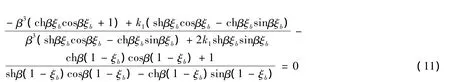
方程(11)是关于未知量β的超越方程，用数值方法如两分法可得到系统的各阶特征值βi。将式(10)代入式(9)中，经过整理和化简后，可得到线性弹簧支承悬臂梁系统振型函数的具体表达式:

其中:

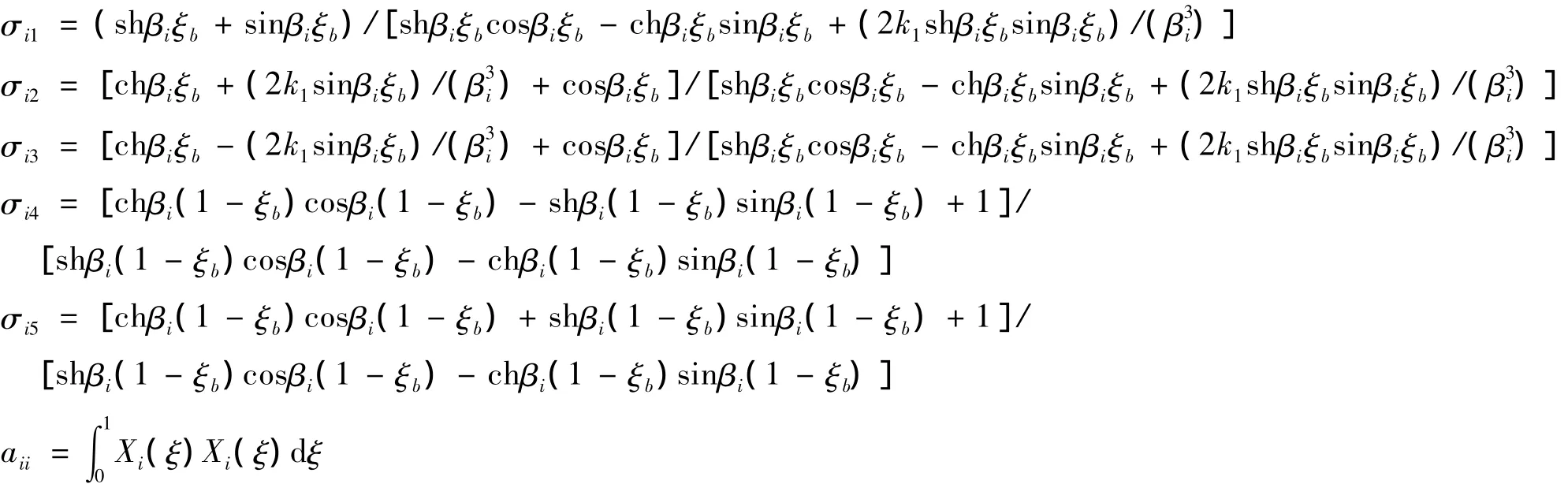
3 输液管道系统运动微分方程的离散化

为便于求解输液管道系统运动微分方程，利用李兹-伽辽金方法将无量纲化的高阶偏微分方程式(8)进行离散化处理并降阶为低次的常微分方程组。为此，采用Galerkin二阶展开式:

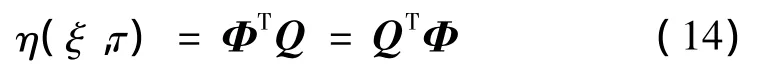
将式(13)、(14)代入式(8)中，得:

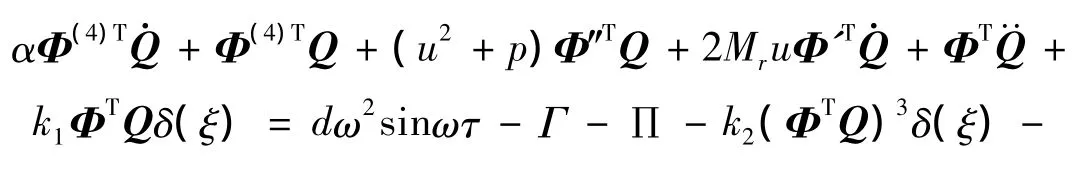
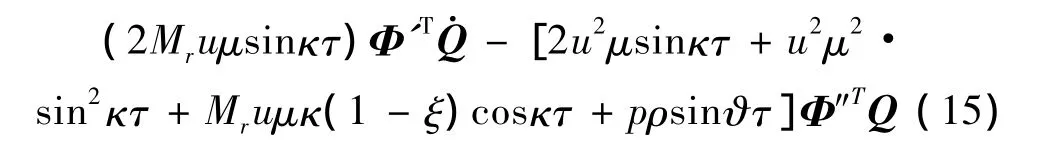
重力只影响振动的平衡位置，对振动的其他特性无影响［9］，令 Γ =Π =0，将式(15)两端左乘 Φ =[ φ1φ2]T，然后在区间［0，1］上进行积分，利用振型函数的正交性［8］和三角函数的正交性以及δ函数的性质，经过复杂的计算整理得:

式中:

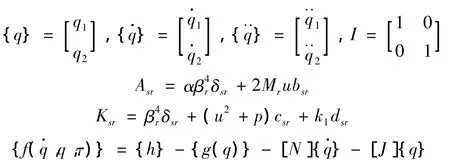
其中:

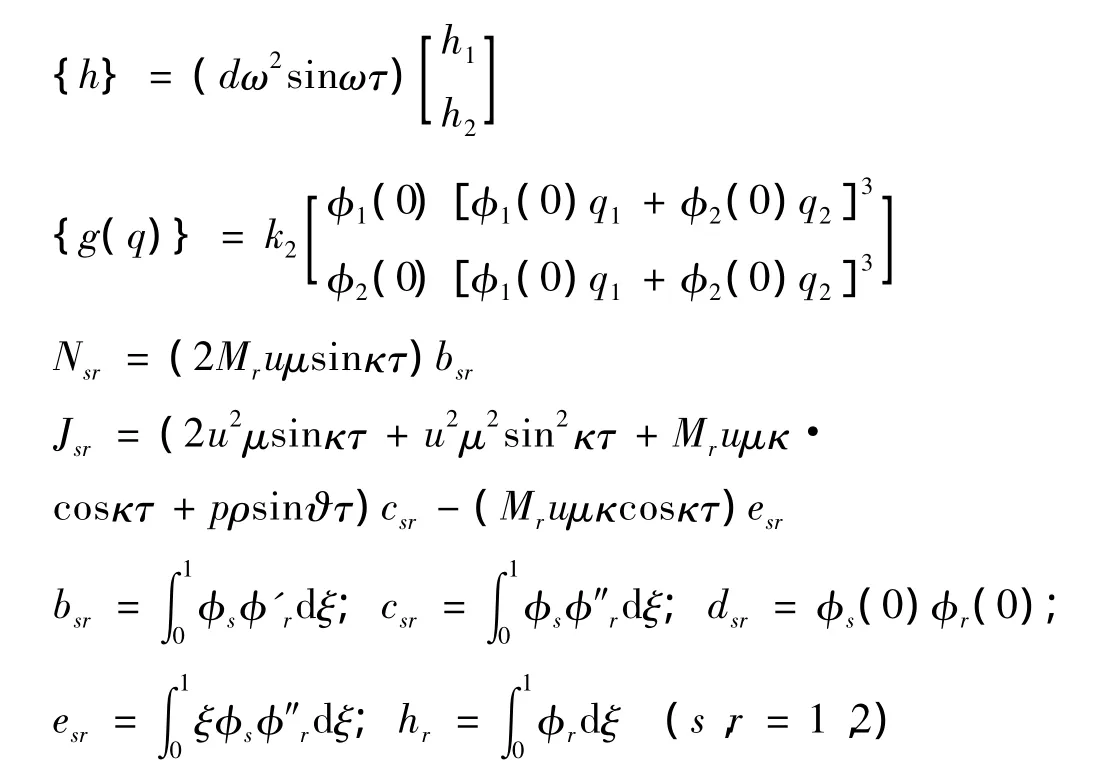
通过引入状态变量将式(16)改写成一阶状态方程组形式。

令:Z=［x1，x2，x3，x4］T=［q1，q2，q3，q4］T，则式(16)可进一步化为:

其中:

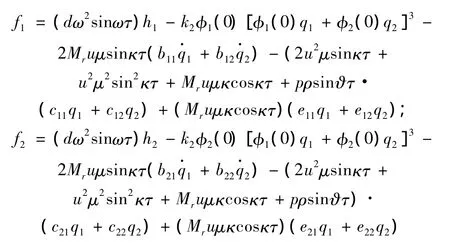
4 数值仿真

在仿真分析中，系统参数为:

对方程组(17)采用四阶Runge-Kutta法进行迭代计算，初始条件取Z1(0)=Z2(0)=-0.001，Z3(0)=Z4(0)=0。

本文分析输液管道系统在流体平均流速参数区域内的分岔过程。在绘制分岔图过程中使用的触发条件是输液管道在中点ξ=0.5位置处的速度趋于零，即:

满足式(18)时在分岔图中记录下此参数激励时管道中点ξ=0.5位置处位移的近似值:

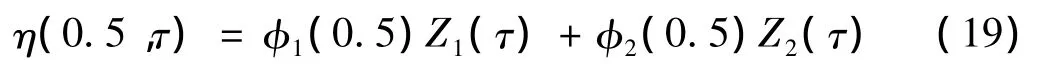
4.1 流体平均流速的影响

以流体平均流速u为控制参数(Mr=0.8)，绘制分岔图(如图3所示)。从分岔图中可以大体上看到非线性弹簧支承悬臂输液管道系统运动的分岔路径。但是还不能显示某些具体的运动形态。因此本文作相图(如图4所示)和功率谱图(如图5所示)来分析系统的的动力学响应。图4与图5中的(a)，(b)，(c)，(d)，(e)，(f)分别对应于控制参数u=5.45，u=5.81，u=6.06，u=6.55，u=7.04，u=7.11。

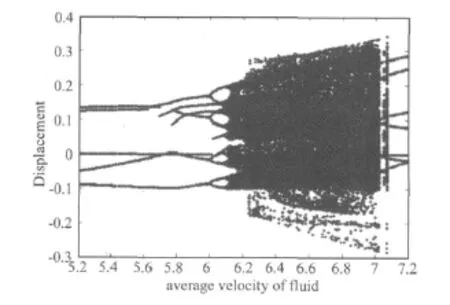
图3 流体平均流速参数区域的分岔图(Mr=0.8)Fig.3 The bifurcation diagram for parameters with average velocity of fluid(Mr=0.8)

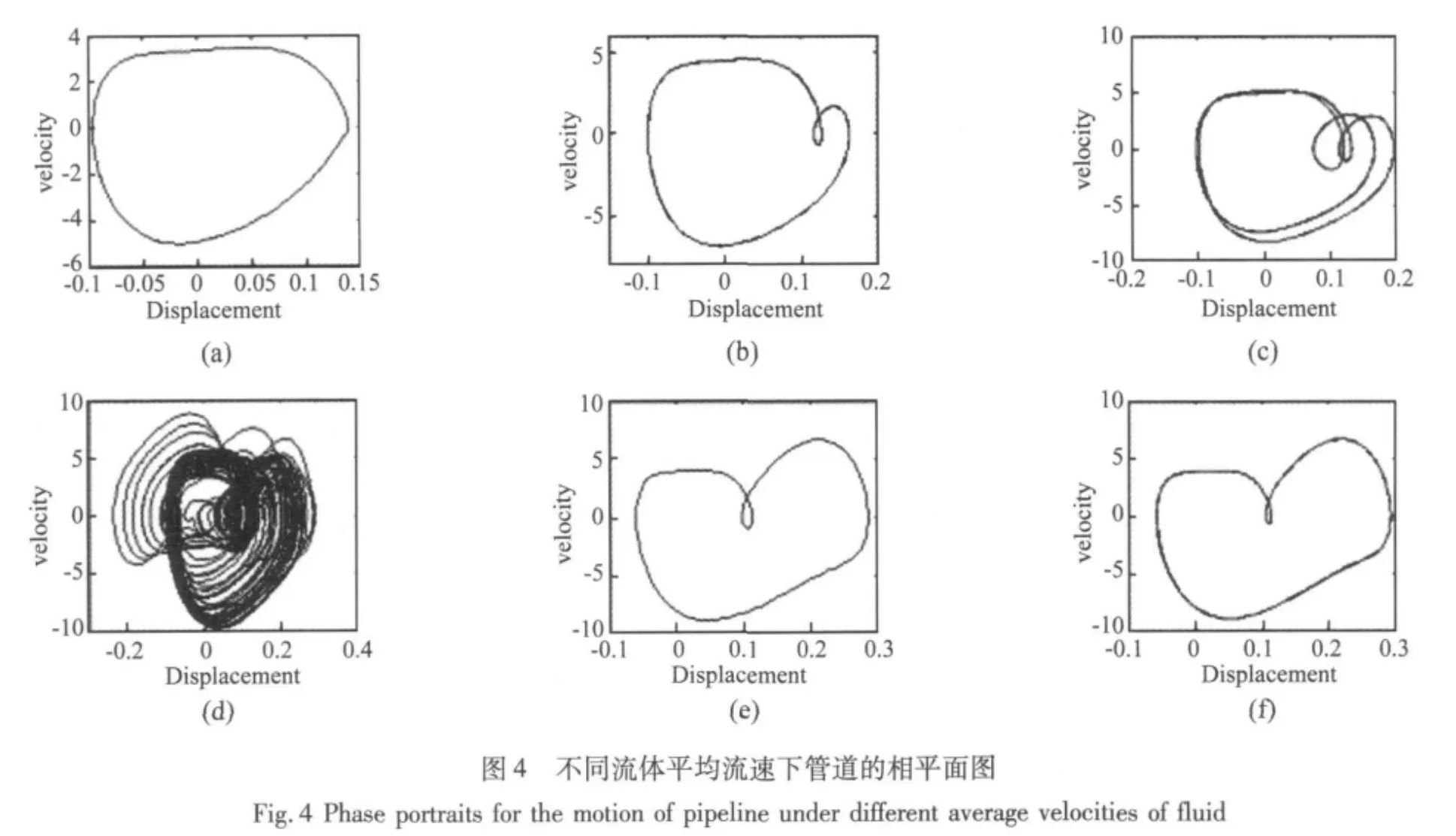
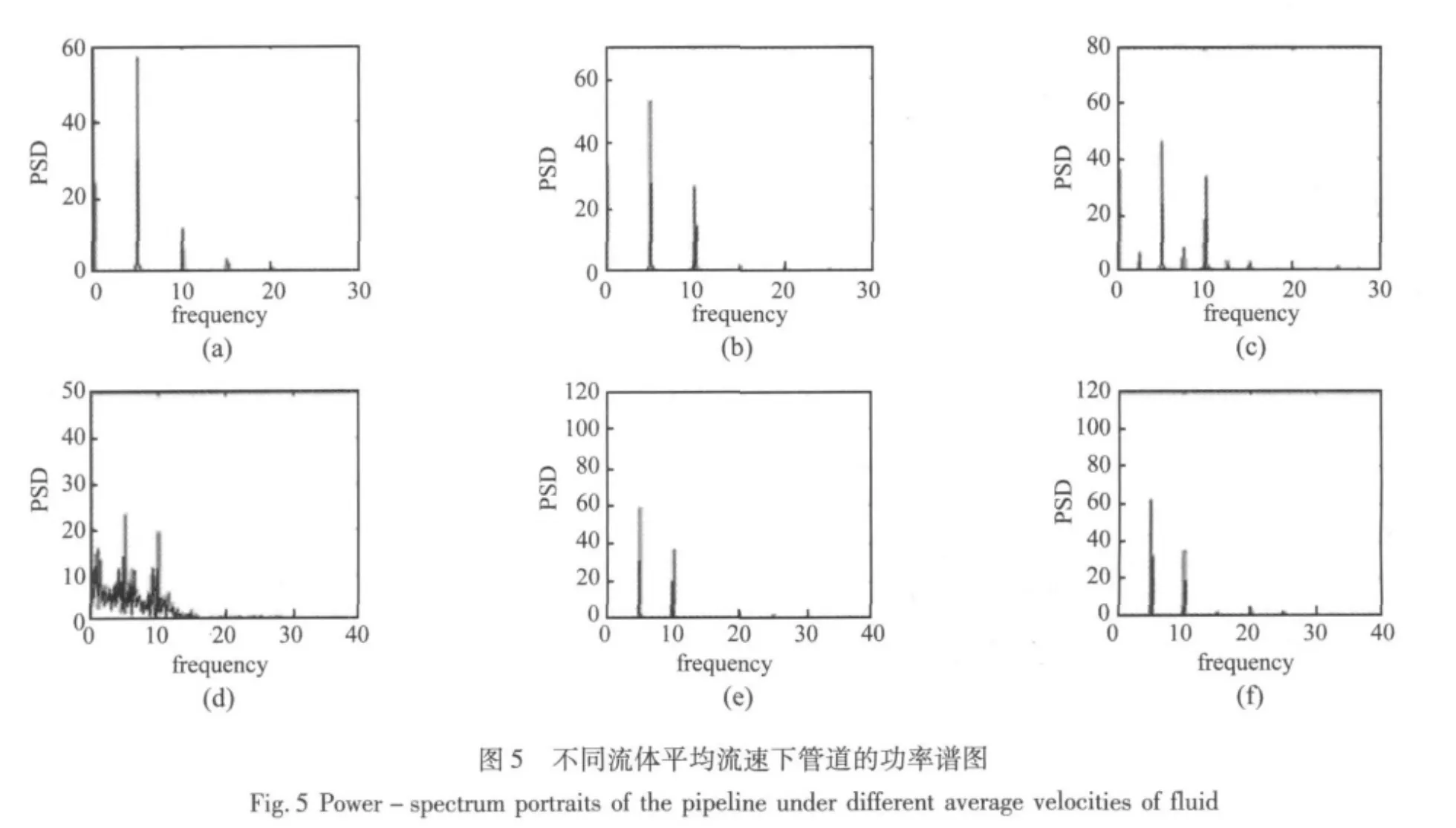
本文利用功率谱曲线图来鉴别混沌和周期运动，即当系统出现周期运动时，功率谱曲线仅有一些狭窄的谱尖点;当系统的运动表现为混沌时，功率谱曲线表现为明显的宽频性质，并且出现了噪声背景。因此从图5的功率谱曲线图以及图3的分岔图和图4的相图可以看出，非线性弹簧支承悬臂输液管道系统对于流体平均流速的运动响应，当流体平均流速较小时，输液管道系统的响应首先表现为周期运动。随着流体平均流速的增大，系统的运动出现系列倍周期分岔，使系统的响应通向混沌运动，随着流体平均流速的进一步增大，系统的运动出现系列倍周期倒分岔转化为周期运动。

4.2 流体与管道质量比对分岔图的影响

取流体与管道质量比参数分别为:

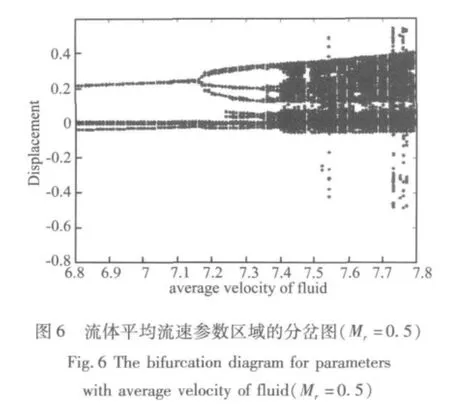
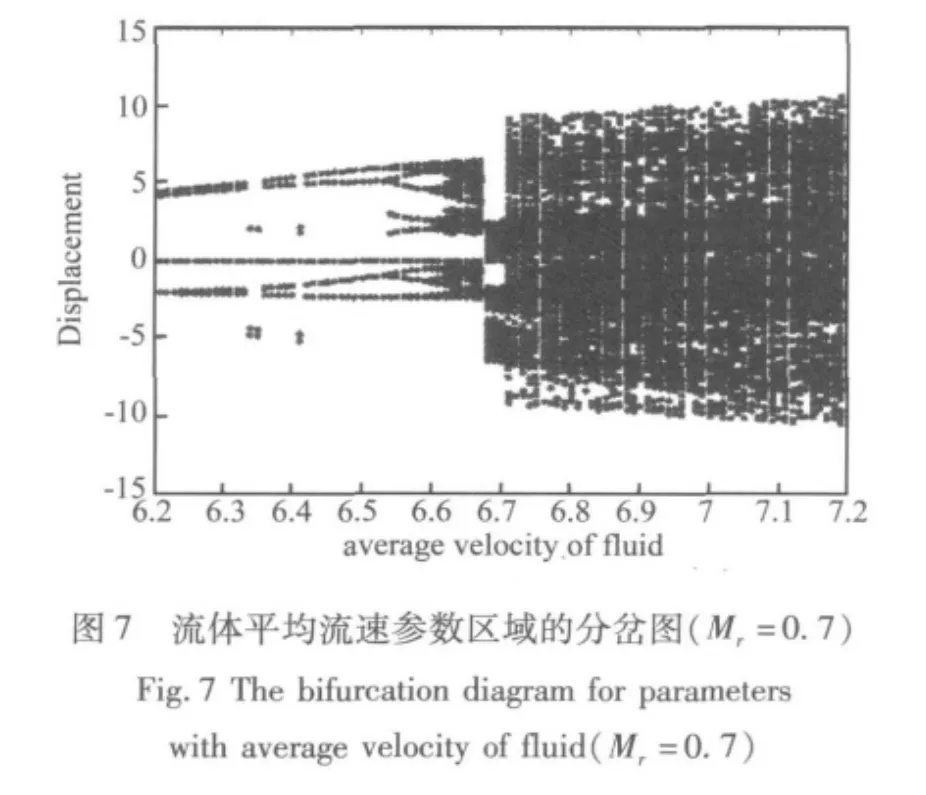
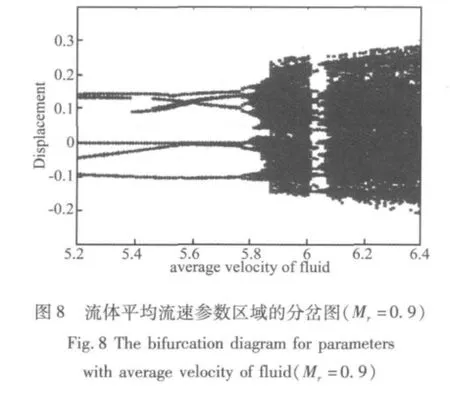
以流体平均流速u为控制参数，绘制分岔图(如图6、图7、图8 所示)。

从图6可以看出，非线性弹簧支承悬臂输液管道系统开始发生混沌运动的临界流体平均流速为u=7.34;从图7可以看出，输液管道系统开始发生混沌运动的临界流体平均流速为u=6.61;从图3可以看出，输液管道系统开始发生混沌运动的临界流体平均流速为u=6.08;从图8可以看出，输液管道系统开始发生混沌运动的临界流体平均流速为u=5.79。因此可以得到随着流体与管道质量比的增大，非线性弹簧支承悬臂输液管道系统开始出现混沌运动的临界流体平均流速值减小。

5 结论

对非线性弹簧支承悬臂输液管道系统在自激励、参数激励和外激励联合作用下的非线性动力学行为进行了研究，得到了流体平均流速和流体与管道质量比变化对输液管道系统的运动影响。当流体的平均流速较小时，输液管道系统的响应首先表现为周期运动，随着流体平均流速的增大，系统的运动出现系列倍周期分岔，使系统的响应通向混沌运动，又经过系列倍周期倒分岔转化为周期运动。另外，随着流体与管道质量比的增大，输液管道系统开始出现混沌运动的临界流体平均流速值减小，所以通过改变质量比参数可以控制输液管道系统的振动形态。为今后分析和研究非线性弹簧支承悬臂输液管道系统的动态响应和振动控制提供理论依据。

［1］ Holmes P J.Pipes supported at both ends cannot flutter［J］.Journal of Applied Mechanics，1978，45:619-622.

［2］ Paidoussis M P，Moon F C.Non-linear and chaotic fluidelastic vibrations of a flexible pipe conveying fluid ［J］.Journal of Fluids and Structures，1988，3:567-591.

［3］ Paidoussis M P，Li G X，Moon F C.Chaotic oscillations of the autonomous system of a constrained pipe conveying fluid［J］.Journal of Sound and Vibration ，1989，135:1-19.

［4］Tang D M ，Dowell E H.Chaotic oscillations of a cantilevered pipe conveying fluids［J］.Journal of Fluids and Structures，1988，2:263-283.

［5］金基铎，邹光胜，张宇飞.悬臂输流管道的运动分岔现象和混沌运动［J］.力学学报，2002，34(6):863-873.

［6］倪 樵，王 琳，黄玉盈，等.谐激励作用下输流曲管的混沌振动研究［J］.固体力学学报，2005，26(3):249-254.

［7］包日东，金志浩，闻邦椿.一般支承条件下输流管道的非线性动力学特性研究［J］.振动与冲击，2009，28(7):153-157.

［8］李 琳，唐 冶，任正义，等.具有弹性支承输流管道的稳定性和临界流速分析［J］.哈尔滨工程大学学报，2010，31(11):1509-1513.

［9］包日东，闻邦椿.微分求积法分析弹性支承输流管道的稳定性［J］.东北大学学报，2007，28(7):1017-1020.

［10］ Jin J D，Zou G S.Bifurcations and chaotic motions in the autonomous system of a restrained pipe conveying fluid［J］.Journal of Sound and Vibration，2003，260:783-805.