箱梁断面气动导数的CFD模拟研究

刘 钥，张志田，陈政清

(1.中国市政工程西北设计研究院有限公司武汉分院，武汉 430056;2.湖南大学 风工程试验研究中心，长沙 410082)

按照风洞试验模型的振动情况来分类，目前所采用的气动导数试验识别方法可分为自由振动法与强迫振动法两大类。近年来，随着计算机技术及计算流体动力学的发展，采用数值仿真的方法识别桥梁气动导数已成为可能。虽然与风洞试验相比，数值方法还存在一定局限性，但数值方法已成为识别桥梁气动导数的另一种方法。Walther借助离散涡法，在气动弹性数值分析方面做了开创性的工作［1］;Larsen基于离散涡法开发了DVMFLOW软件，数值计算了从流线型至H型逐渐变化的5种典型桥梁断面的气动导数［2］;曹丰产用有限单元法求解二维不可压粘性流体的N-S方程计算运动物体的气动力，识别了几种典型桥梁断面的气动导数［3］;周志勇采用离散涡法，提取了南京二桥闭口箱梁断面的气动导数［4］;祝志文通过有限体积法对桥梁断面的气动导数及颤振临界风速进行了数值模拟［5］，张倩采用计算软件FLUENT，在桥梁气动导数的计算方面提出了刚性边界层网格+三角形动网格+静止网格的网格分区方法［6］;辛大波分别采用了Fluent中的RNGk-ε和Realizablek-ε两种湍流模型识别了气动导数［7］;刘慕广采用动网格强迫结构简谐振动，识别了薄平板、大带东桥及腹板开孔H型截面的气动导数［8］。

本文在对某大桥跨中箱梁断面0°攻角下的气动导数进行数值识别前，先通过商用CFD软件，采用动网格法强迫模型运动的方式对薄平板的气动导数进行了数值识别并与试验结果进行了对比，验证CFD数值识别的可行性，随后以跨中箱梁断面模型为原型，提取了8个气动导数，并与强迫振动试验法得到的气动导数结果进行了对比。

1 薄平板气动导数

图1 薄平板模型(mm)Fig.1 Model of thin flat plate(mm)

薄平板计算模型尺寸如图1所示，宽高比为22.5，模型计算域为二维矩形，入口距平板模型中心为5B(B为平板模型宽)，出口距模型中心为10B，上下距模型中心各为5B。不同雷诺数时数值试验研究所需要的网格精细程度也不同，主梁壁面的第一层网格需要满足y+≈1。可以用下面的公示估算y+，并确定第一层网格控制点离壁面的距离 Δy(Schlichting，1979):y+=0.172Δy/LRe0.9。由于主梁断面在风洞试验时很难知道雷诺数的大小，于是采用 Δy试算法得出Δy已满足y+≈1这一条件。采用ANSYS ICEM CFD 10.0生成计算网格，构造网格时仅采用结构网格，靠近物面的第一条网格线距物面距离为Δy=0.09 mm，即0.000 2B，以1.3的生长率径向逐渐放大网格(图2)，共生成了2.82万左右的结构网格。

采用ANSYS CFX 10.0进行边界条件给定及数值计算。入口为速度边界条件，即Vx=6 m/s，Vy=0 m/s;出口为压力边界条件，参考压力为零;上下面采用自由滑移壁面条件，即Vx=6 m/s，Vy=0 m/s;主梁断面结构表面采用无滑移壁面条件，即Vx=0 m/s，Vy=0 m/s;侧壁采用对称边界条件。

模型作竖向振动的振幅为0.02B，作扭转运动的振幅为2°。首先固定平板模型做定常计算，然后以此为初场使平板强迫振动，进行非定常计算，计算中采用SST湍流模型。通过变化模型振动频率的方式来提高无量纲风速，计算采用的时间步长为0.002 s，共计算得到了10 s内的气动力时程曲线。

图2 计算网格Fig.2 Meshing of thin flat plate

图3 数值模拟时的气动力时程曲线(U/fB=10)Fig.3 Aerodynamic forces time-history curves in CFD(U/fB=10)

图3为无量纲风速U/fB=10，薄平板分别数值模拟时做竖向与扭转运动前10 s时气动力时程，图4和图5为平板竖向运动和扭转运动时压力等高线及流线图。由图3可见，薄平板强迫运动产生的气动自激力谐波特性极好。由图4中的流线图看见，平板模型在竖向运动过程中无明显尾流分离区，尾流中也没有旋涡的脱落与运动，这跟平板宽高比为22.5，较好的流线性有关。

从图4和图5中的薄平板时程升力曲线最后一周期内涡脱压力等高线图可以看出，在t=0时，薄平板上顶面和下底面的压力等高线相互对称，上下压力相互抵消，此时薄平板对应的升力为平均值，其值接近于0;在t=1/4T时刻，下底板的绝对值大于上顶板，此时升力达到最大值;在t=1/2T时刻跟t=0时刻一样，此时升力为平均值;在t=3/4T时刻，下底板的绝对值小于上顶板，升力达到最小值。从图中我们可以看出t=0时刻跟1/2T时刻、t=1/4T时刻跟t=3/4T时刻对应的压力等高线恰好成镜像关系。

图6中的试验结果为采用强迫振动法识别出的平板气动导数值，由图识别结果可以看出:

(4)由以上平板数值方法识别结果可以看出，采用CFD动网格法识别颤振导数的合理性及采用数值方法识别桥梁颤振导数可行。

2 桥梁箱形断面的气动导数

某大桥是一混凝土刚构桥，主梁跨中断面模型宽B=0.3 m，数值计算时没有考虑栏杆等附属物。计算域同样为二维矩形，入口距模型剪心为5B(B为桥面宽)，出口距剪心为10B，上下距剪心各为5B。靠近物面的第一条网格线距物面距离为Δy=0.000 5 m，即0.001 7B，满足y+≈1这一条件，并以1.3的生长率径向逐渐放大网格(图6)，共生成了3.02万左右的结构网格。

计算域入口为边界条件与前面平板计算模型设定一致。模型做竖向振动的振幅为0.015B，做扭转运动的振幅为2°。首先固定模型做定常计算，然后以此为初场，进行非定常强迫振动计算，湍流模型为SST模型。通过变化模型振动频率的方式来提高无量纲风速U/fB，计算采用的时间步长为0.002 s，共计算得到了前10 s的时程曲线。

由图8可看出，气动力波形没有薄平板那样有规则，由于跨中断面分离流较为复杂，气动力信号中含有较多的干扰成份。宽高比为3.43的跨中断面与薄平板模型明显的区别在于，跨中断面存在一个尾流分离区，且分离区的大小及位置随断面运动而变化，故跨中断面的压力等高线分布比平板也要复杂一些。图9和图10为断面竖向和扭转运动时对应一个周期内压力等高线及流线变化。

从图9中的跨中断面升力时程曲线最后一周期内涡脱压力等高线图和流线图可以看出，在t=0时，箱梁上顶板和下底板附近的尾流出现速度旋涡，此时对应地在下底板后缘的尾流出现压力旋涡;在t=1/4T时刻，箱梁上顶板出现速度旋涡，尾流的速度旋涡向下游运动，此时对应地在离下底板较远的地方出现压力旋涡，且在上顶板后边缘有形成压力旋涡的趋势;在t=1/2T时刻，箱梁上顶板和下底板附近的尾流出现旋涡，此时对应地在上顶板和下底板的后缘出现压力旋涡;在t=3/4T时刻，箱梁上顶板和下底板附近的尾流出现旋涡，下底板后缘的旋涡逐渐增大并有向下游运动的趋势，此时对应地在上顶板和下底板的后缘出现压力旋涡，两个旋涡都向下游运动。

从图10中跨中断面升力时程曲线最后一周期内涡脱压力等高线图和流线图可以看出，在t=0时，离箱梁较远的尾流出现速度旋涡，此时对应地在后缘的尾流出现压力旋涡;在t=1/4T时刻，箱梁上顶板后缘出现速度旋涡，尾流的速度旋涡向下游运动，此时对应地在上顶板后缘和离下底板较远的地方出现压力旋涡;在t=1/2T时刻，箱梁上顶板和下底板附近的尾流出现旋涡，此时对应地在上顶板和下底板的后缘出现压力旋涡;在t=3/4T时刻，箱梁下底板后缘和离上顶板较远的尾流出现旋涡，此时对应地在箱梁下底板后缘和离上顶板较远的尾流出现压力旋涡。

图9 箱形断面竖向运动时的压力等高线与流线Fig.9 Streamlines and pressure contour lines around box girder within a cycle as the vertical movement of mesh

图10 箱形断面扭转运动时的压力等高线与流线Fig.10 Streamlines and pressure contour lines around box girder within a cycle as the torsion movement of mesh

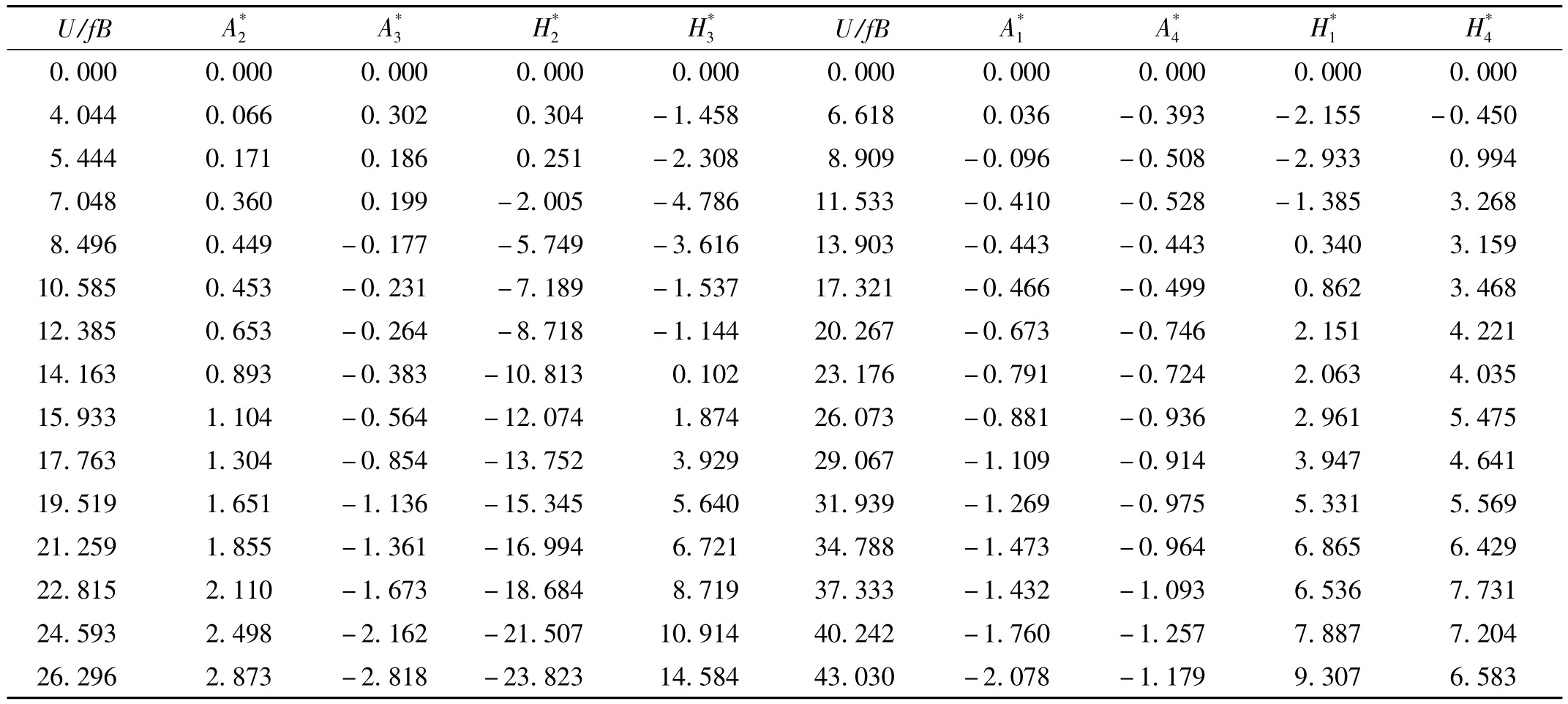
表1 某大桥箱形断面的气动导数Tab.1 Aerostatic derivatives〛of one long －span bridge’s box girder

表2 某大桥箱形断面的气动导数Tab.2 Aerostatic derivatives of one long － span bridge’s box girder

跨中断面气动导数的试验结果如表1所示。跨中断面气动导数的数值模拟结果如表2所示。数值模拟方法识别到的跨中断面气动导数如图11所示，图中试验值为强迫振动法得到的气动导数结果。

图11 箱形断面颤振导数Fig.11 Aerostatic derivatives of box girder

3 结论

本文通过CFD数值模拟结合强迫振动风洞试验识别了薄平板、主梁跨中断面的气动导数。结果表明:

(1)对流线性好的薄平板，CFD数值计算气动导数值与理论解曲线吻合良好。

(2)钝体箱形断面数值识别结果与试验值存在一定误差。由于分离流与旋涡的复杂性，数值模拟结果在低折减风速更接近试验值，而在高折减风速，差别较为明显。识别精度与数值计算中网格密度及时间步长紧密相关。

(3)跨中断面识别的气动导数与试验值吻合程度较好，结合薄平板的识别结果可见，数值方法强迫模型运动提取气动导数的过程受模型本身流线程度和离散网格质量的影响较大，断面流线型越好，网格质量越高，数值模拟识别得到的气动导数精度就越高。

(4)从气动导数的趋势来看，CFD计算结果与风洞试验有较好的一致性。但对于钝体特性十分明显的桥梁箱形断面，目前采用CFD方法识别气动导数存在明显不足之处，尤其是算法的稳定性及效率问题。因此，对于钝体特性十分明显的断面，CFD方法目前尚不能完全取代物理风洞研究其流固耦合问题。

［1］ Walther J H，Larsen A.Two dimensional discrete vortex method for application to bluff body aerodynamics［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67-68:183-193.

［2］Larsen A，Walther J H.Aeroelastic analysis of bridge girder sections based on discrete vortex simulations［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67-68:253-265.

［3］曹丰产，项海帆，陈艾荣.桥梁断面气动导数和颤振临界风速的数值计算［J］.空气动力学学报，2000，18(1):26-33.

［4］周志勇，陈艾荣，项海帆.涡方法用于桥梁断面气动导数和颤振临界风速的数值计算［J］.振动工程学报，2002，15(3):327-331.

［5］祝志文，陈政清.数值模拟桥梁断面气动导数和颤振临界风速［J］.中国公路学报，2004，17(3):41-45.

［6］张 倩，廖海黎.桥梁主梁断面气动力特性的数值模拟研究［J］.工程结构，2008，28(4):83-86.

［7］辛大波.基于数值方法的大跨桥梁颤振分析［D］.哈尔滨:哈尔滨工业大学，2004，1-82.

［8］刘慕广.两类大长细比桥梁构件的风振特性研究［D］.长沙:湖南大学，2009，1-169.