某轿车排气系统振动分析
2011-02-13刘敬平邓帮林冯仁华许胜利
刘敬平,邓帮林,杜 标,冯仁华,许胜利
(1.湖南大学 先进动力总成技术研究中心,长沙 410082;2.湖南奔腾动力科技有限公司,长沙 410082)
排气系统一端与发动机相连,另一端通过吊耳和车体相连。激励源的振动传递给排气系统,然后再通过吊耳传递给车体,车体的振动通过座椅、方向盘和地板直接传递给乘客,同时车体的振动也会辐射出去,在车内产生噪声[1]。所以,排气系统吊耳的动刚度是确定排气系统对汽车NVH性能的影响因素之一[2]。吊耳的动刚度不能过高,否则不利于吊耳隔振。同时吊耳的动刚度不可过低,过低的动刚度虽可提高隔振率,但会导致吊耳产生较大的静变形,对吊耳的耐疲劳性能有不利影响[3,4]。本文在已知吊耳动刚度的前提下研究排气系统本身的振动,不着重研究吊耳。
排气系统的激励源主要有五个[5]:发动机的机械振动、路面的随机激励、发动机的气流冲击、声波激励和车体振动。第一,发动机的机械振动,排气系统直接和发动机相连,因此发动机的振动可以直接传递给排气系统。第二,路面谱的随机激励,路面随机激励通过轮胎、车体和发动机等传递给排气系统,然后排气系统逆向传递给车体。第三,发动机的气流冲击,高速气流经过汽缸排出,直接激励排气多支管,从而引起排气系统振动。第四,声波振动,声波在管道内运动时,会对管道和消声器等产生冲击,因而引起振动。第五,车体的振动,这个振动传递方向与前面传递相反,车体振动也会通过吊耳传递到排气系统,然后逆向传递到发动机,从而加大发动机的振动。
由于后三种激励难以用理论和数值描述,同时,前两种振动激励源对排气系统的影响较大,由于条件的限制,本文仅考虑发动机激励。
相对于国外的研究,国内对排气系统的研究相对较晚,研究内容也相对较浅。国外对排气系统建模的研究主要集中在排气系统组件和排气系统整体建模两方面,文献[6-8]对排气系统振动、噪声、疲劳、排放、振动传递函数、敏感度和吊挂力学行为等进行了相关分析和论述。相对于车辆悬挂系统、传动和制动系统的研究,排气系统动力学研究较少,Goktan等[9]建立了包含排气系统的半车模型,对路面谱的振动传递特性进行了研究。而整个排气系统与发动机本体耦合进行多体动力学(刚柔结合)分析的研究较少见,本文正是着手此方面的研究。
1 排气系统组成及吊耳位置分布
该排气系统由排气歧管、增压系统、前后消声器、催化转换器、管路和吊耳等组成,如图1所示,为了后续叙述的方便,把四个吊耳点分别命名为A、B、C和D。许多文献里陈述了关系排气系统设计的一些准则,最常用的是吊耳的位置选取[6,7]。
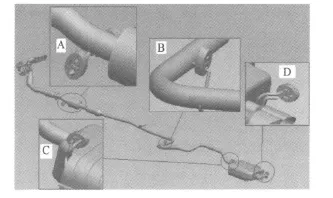
图1 排气系统组成及吊耳分布Fig.1 The composition of exhaust system and hanging distribution
2 排气系统自由模态分析
典型的无阻尼模态分析求解的基本方程是经典的特征值问题:
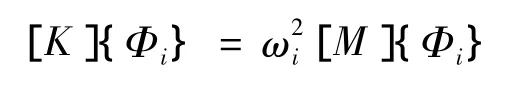
其中:
[K],刚度矩阵;
{Φi},第i阶模态的阵型向量(特征向量);
ω,第i阶模态的固有频率是特征值);
[M],质量矩阵。
有限元软件提供了多种方法求解上面的方程,其中分块Lanczos法特征值求解器是缺省求解器,它采用Lanczos算法,是用一组向量来实现Lanczos递归计算,这种方法和子空间法一样精确,但速度更快。计算某系统特征值谱所包含一定范围的固有频率时,采用分块Lanczos法提取模态特别有效。计算时,求解从频率谱中间位置到高频端范围内的固有频率时的求解收敛速度和求解低阶频率时基本上一样快。因此当采用频移频率(FREQB)来提取从FREQB(起始频率)的n阶模态时,该法提取大于FREQB的n阶模态和提取n阶低频模态的速度基本相同。
表1为排气系统前6阶固有频率及振型说明,由于此排气系统跨度较大,总体为细长杆结构,结构刚度偏低。图2~图7为排气系统1~6阶振型图。通常,吊耳是放在节点的位置,模态节点的振动在理论上是零,这样可以有效的减少排气系统对车体的振动传递率。但是实际设计中,排气系统模态的节点在数值仿真中并不容易确定,同时由于车体下部结构布局的限制,吊耳具体位置的确定需要设计者根据具体问题具体分析,不能一概而论。下面结合模态分析来分析吊耳位置的布置合理性。
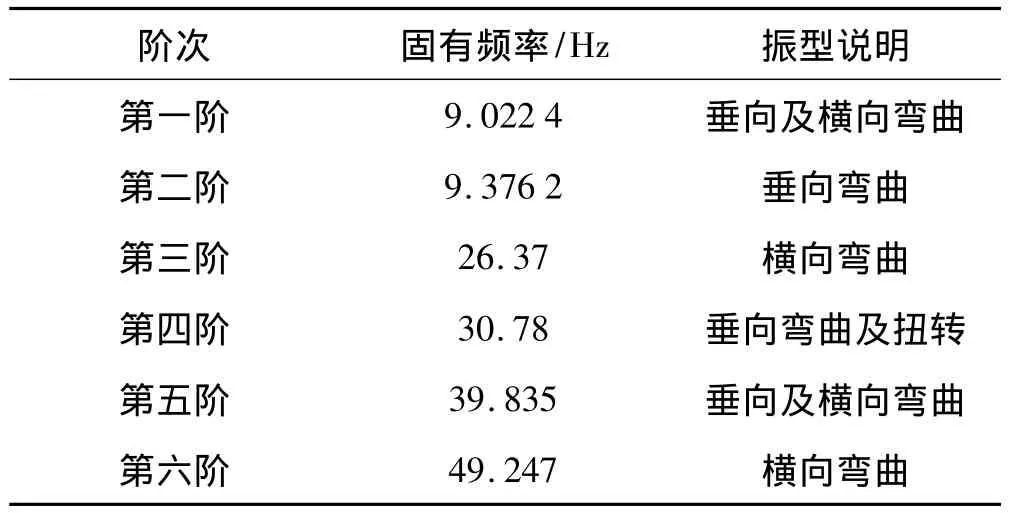
表1 排气系统各阶固有频率及振型说明Tab.1 Natural frequencies of exhaust system and mode shapes description
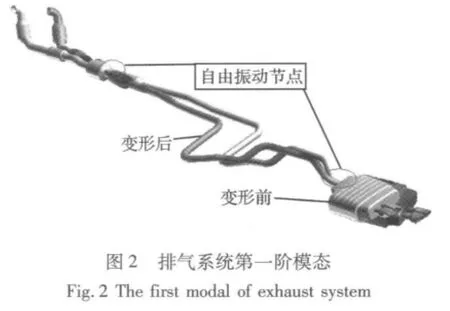
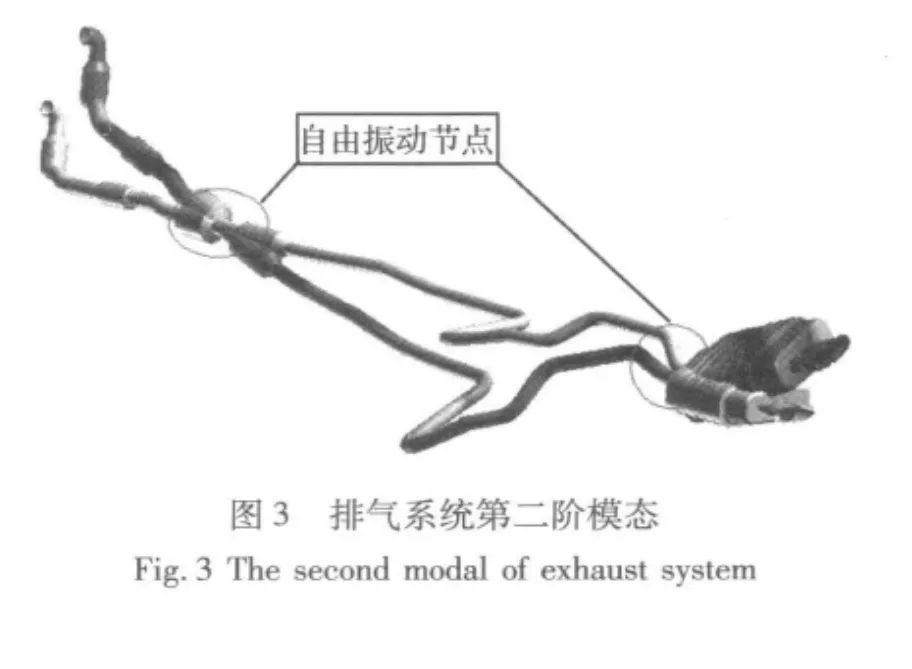



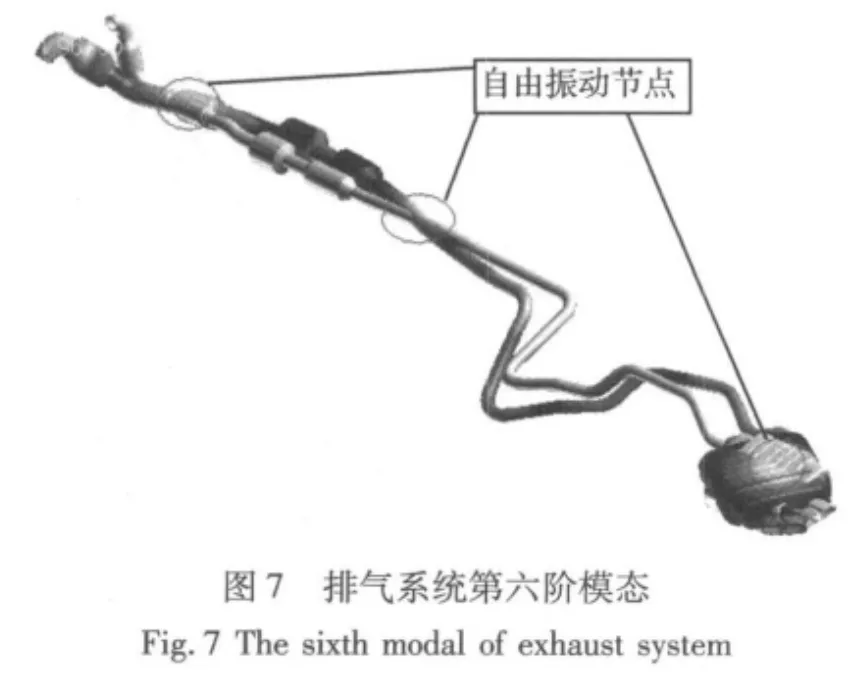
第一阶模态有两个节点,分别出现于吊耳A及C附近;第二阶模态也两个节点,同样位于吊耳A及C附近;第三阶模态单个节点,位于吊耳C附近;第四阶模态出现三个节点,其中前后两个分部出现于吊耳A及C附近;第五阶模态出现单个节点,未靠近任何吊耳;第六节模态出现三个节点,其中前后两个分部出现于吊耳A及C附近;纵观前六阶模态,吊耳A及C基本布置在节点附近,较合理。而吊耳A和C之间跨度较大,为细长结构,除第四、第六阶外(出现的节点离吊耳B较远),其他阶次未出现节点,可通过改变排气管走向及改动吊耳B位置来协调自由振动模态及吊耳位置的关系。吊耳D处于尾端,不可避免的处于振动剧烈区。
纵观前六阶模态,有三阶出现两个方向上的振型耦合,可以想见,对于后续的高阶模态,各方向上的振动耦合会加剧,这对于结构复杂、跨度较大的排气系统很难避免,这也说明排气系统的振动是各方向耦合的复杂动力学行为。
在排气系统模态分析时,通常要对下面几个指标设定为目标:第一阶垂向弯曲模态、第一阶横向弯曲模态、第一阶扭转模态和模态密度。第一阶垂向弯曲模态和第一阶横向弯曲模态是排气系统中最容易被发动机激励起的模态,同时,这两个模态的振动也最容易传递到车体并与车体发生共振。因此,这两个模态的频率目标是:与发动机的激励频率错开,与车体的固有频率错开。本例当中,由于前几阶整体模态频率较低,可避开发动机激励频率(但在低频区域,发动机的半倍频或者四分之一倍频可能是主要的激励源,因此在振动设计中应该给予重视),但是否会避开车体的固有频率还需进一步对车体进行模态分析;在四轮驱动和全轮驱动的汽车中,排气系统有时候与传动轴系共用支撑架,因此排气系统的频率也必须与传动轴的频率分开。
同时,在设计排气系统时,要使得其模态数目越少越好。如果模态数目越多,那么系统的某些模态很容易被激励起来,振动容易被传递到车体。本例当中,第一阶和第二阶模态太靠近。另外,排气系统应该被尽可能地设计成为一条直线,避免弯曲的形状。笔直的排气系统不仅模态数目少,容易控制,而且气体在管道中流动通畅,背压小,功率损失就小。
3 排气系统受迫振动分析
3.1 多体动力学模型建立
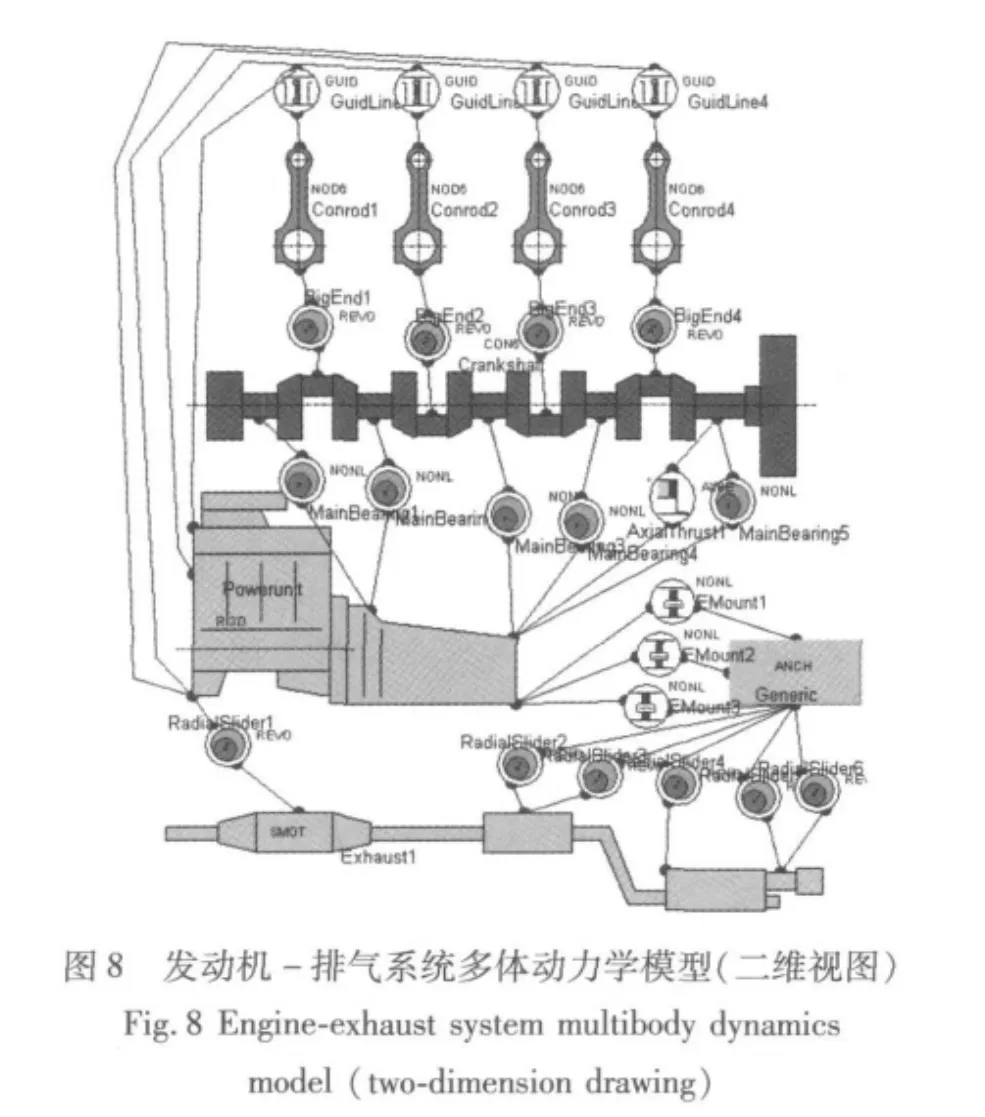
利用AVL-EXCITE建立发动机多体动力学模型,如图8所示。其核心为曲柄连杆机构,爆发压力通过曲柄连杆机构传递到主轴承,进而作用在动力总成上,此次计算就是为了考查排气系统对由此引起的激励的振动响应。图9为其三维显示界面,通过此界面,可形象地看到建立的模型正确与否,各零件的耦合关系正确与否。此次计算中,曲轴采用实体单元弹性体,连杆为梁单元弹性体,排气系统为实体单元弹性体,而动力总成为刚形体,车体为不动体。
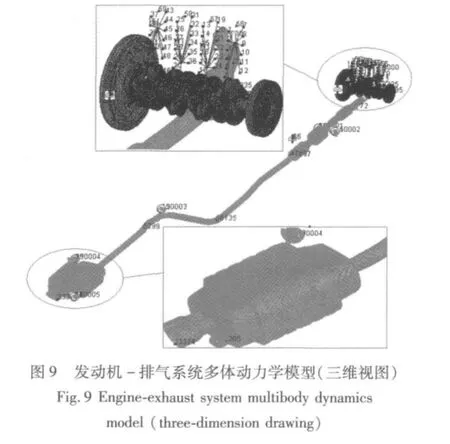
3.2 边界条件
在MSC-Patran中用RBE2单元来耦合排气系统入口,以和发动机上相对应的点连接,如图10,其中 H点为排气系统入口,各吊耳同样用RBE2单元与车体连接。

图10 连接点处理及排气系统入口点示意Fig.10 Connection point processing and intake point indication of the exhaust system
在多体动力学计算中,还需要各种零件属性参数及运行参数:
① 缸径Χ行程Χ缸心距,连杆长度等;
② 活塞(包括活塞环、活塞销)质量、连杆质量及其分配等;
③ 各轴承刚度(经验公式估算)及间隙,各连接副刚度等;
④ 动力总成质量属性(质量、质心位置、转动惯量等);
⑤ 悬置刚度及阻尼等;
⑥ 缸内爆发压力(外特性上各转速),见图11(由于曲线太密,只选取两个转速为代表);
⑦ 机油型号及属性,本例选取机油型号为SAE10W。
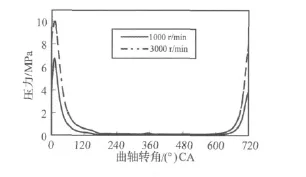
图11 缸内爆发压力曲线Fig.11 The explosion pressure curve in cylinder
3.3 振动响应分析
为了充分了解排气管路的振动响应,在排气管路上选取四个点为考查点,分别为N、O、P、Q,如图12所示,其中Q点位于排气最尾端。
图13~图24为点N、O、P、Q在三个方向上的加速度响应频瀑图。图中加速度单位为m/s2。结合频瀑图,从以下几方面分析:
(1)从频率分布来看,各点加速度主要集中在低频段,相对高频的振动加速度集中于高速。而且,发动机半倍频甚至1/4倍频激励对排气系统振动有较大的贡献。点O的Y方向振动频段分布相对较广泛,说明此点的横向振动频率成份较其他点要复杂。Q点(最尾端点)在三个方向上加速度基本都集中于一窄带频段,频率范围较窄,说明发动机激励传到此处已被大大削弱,频率成份也被滤窄。总之,振动响应的频率成份由排气系统固有频率及激励频率成份决定,还受吊耳布置位置的影响;
(2)从转速范围来看,加速度最大值基本出现于3 000~4 000 r/min之间,这主要受爆发压力的影响,还受发动机工作频率的影响;
(3)从各振动方向来看,前两点(N、O)在X、Y、Z方向上依次增大,特别Z方向远大于其他方向。因Z方向是发动机作用力主方向,说明前两点受发动机激励的方向性影响较大,与发动机受力保持了一致的方向性;后两点(点P、Q)情况要复杂些,各方向振动幅度较接近,在方向上有一定的随机性,此两点振动形式几乎是在以原点为圆心,幅值为半径的圆内运动(最后一点更具此特性)。说明发动机激励经过排气系统复杂的路径传递到后端时,方向已模糊,不再与发动机受力方向保持一致;
(4)所选取的四个考查点,从前至后,振动幅度先加强再减弱,到Q点时,振幅远比前端小,进一步说明了发动机激励从前至后传递时被大大削弱。幅度最大的为O点,因O点处于跨度较长的两吊耳之间,且靠近发动机端,振动最为剧烈。说明各点的振动响应,除受与发动机的远近影响外,还受排气系统具体结构及吊耳位置有关;
总之,振动响应频瀑图可从频段及转速域全面地了解各点的振动响应,为振动诊断提供了有力的分析依据。













3.4 振动传递率分析
由前面的分析可知,排气系统在Z方向(主方向)的振动最剧烈,故传递率分析只对Z方向进行分析,传递率采用以下的公式计算:

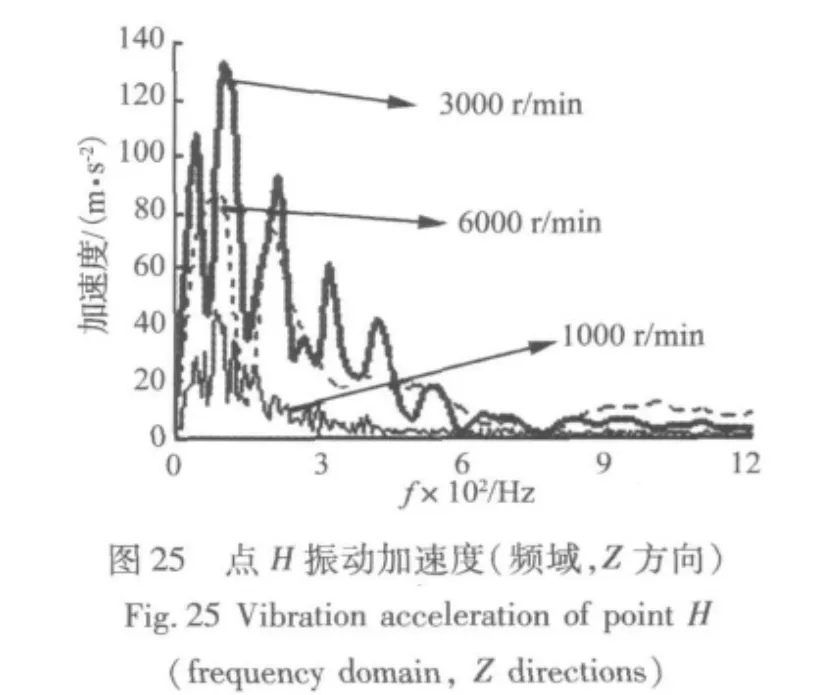
其中,aa为主动边加速度,ap为被动边加速度。aa、ap都取为H点的数值,如图25所示。
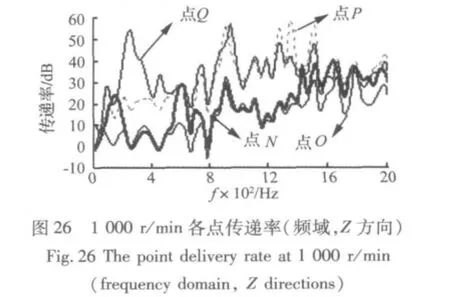
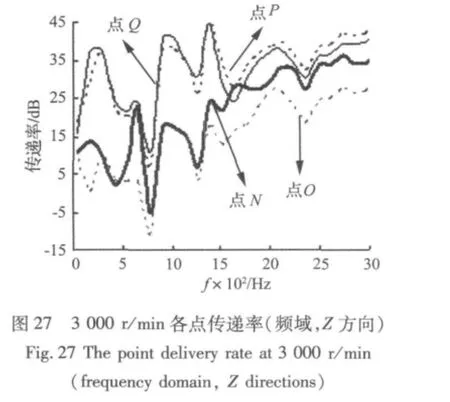
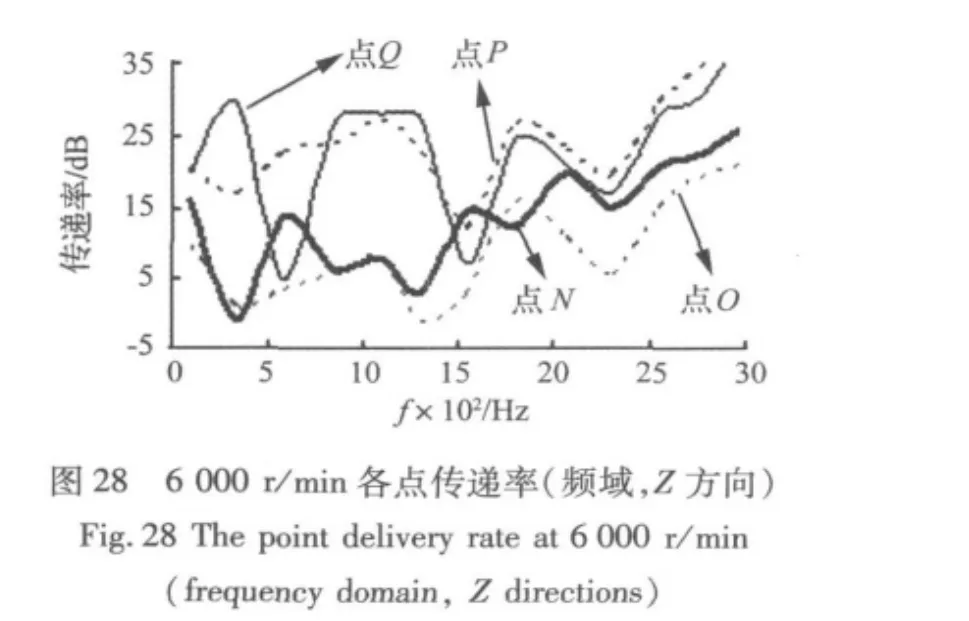
图26~图 28分别为 1 000 r/min、3 000 r/min、6 000 r/min各点的传递率。从各曲线上看,得出以下几点:
(1)各点传递率都不是直线(相同的点在转速上也有差别),波动较大,说明各点的响应是非线性的,振动输出与输入有关,进一步说明了排气系统的振动是高度非线性的复杂动力学行为;
(2)各点传递率皆出现负值(特别在低频段),各点有振动比H点振动加剧的频率段,说明各点之间有振动耦合(振动从前端传往后端,但后端振动亦会影响前端),而后两点(P、Q)明显比前两点(N、O)出现负值的情况要少,说明前两点振动受前后端的耦合较严重,而后端振动已大大减弱,耦合程度也较弱;
(3)从数值上看,越往后传递率越大,也说明了从前至后振动在逐渐衰减,而且后端的传递率数值较大,说明振动经过排气系统的“长途奔袭”,到后端已是“强弩之末”。
4 结论
综合以上分析,得出以下结论:
(1)排气系统固有频率偏低,说明整体结构刚度偏低,而且第一、二阶模态过于接近;
(2)吊耳A和C布置较合理,吊耳B和D可进一步结合结构及排气管走向重新分析;
(3)排气系统的振动响应主要集中在低频段,在长度方向上,前端与发动机受力保持了较好的方向性,而后端响应已模糊了方向;
(4)排气系统的振动传递表现为高度非线性,且在长度方向上存在相位滞后。在长度方向上,从前至后振动在逐渐衰减,但排气系统的跨度较大,中间某些部位受到前后端的振动耦合会出现振动加剧的现象。
[1]李松波.车辆排气系统振动建模与动力学特性研究[D].上海:上海交通大学,2008.
[2]上官文斌,黄 志,贺良勇,等.汽车排气系统吊耳动刚度优化方法的研究[J].振动与冲击,2010,29(1):100-102,152.
[3] Lee C M,Park S T.Development of a simple numerical method of the exhaust system to find optimized design values[J].SAE Paper,1999-01-1666.
[4] Eads K,Haghighi K,Kim H J,et al.Finite element optimization of an exhaust system[J].SAE Paper,2000-01-0117.
[5]庞 剑,谌 刚,何 华.汽车噪声与振动 -理论与应用[M].北京:北京理工大学出版社,2006.
[6] Ling S F,Pan T C.Vibration isolation of exhaust pipe under vehicle chassis[J].International Journal of Vehicle Design,1994,15:131-142.
[7] Pang J P,Kurrle M,Qatu R,et al.Attribute analysis and criteria for antomotive exhaust system[J].SAE Paper,2003-01-0221.
[8]Eads K,Haghighi K.Finite element optimization of an exhaust system[J].SAE Paper,2000-01-0117.
[9] Goktan A G,Yetkin A.A mathematical model for exhaust system vibrations caused by road surface inputs[J].SAE Paper,2001-01-1006.