基于有限振动信号的某移动天线有限元风荷载动力反应分析
2011-02-13刘晶波王宗纲费毕刚王潜渊
刘晶波,郭 东,王宗纲,费毕刚,王潜渊
(1.清华大学 土木工程系,北京 100084;2.清华大学 结构工程与振动教育部重点实验室,北京 100084;3.中国移动通信集团 北京分公司,北京 100007)
风荷载是建筑物的主要荷载之一,它与地震荷载一样是建筑结构常遇的水平荷载。对于高层、高耸结构和大跨度结构,风荷载引起的效应在总荷载效应中占有相当大的比重,甚至起决定性作用,因而风荷载及风荷载作用下结构的静、动力反应常常是高层、高耸及大跨结构研究的主要内容。目前我国的研究多是基于测压试验来进行[1-4]。对高耸结构类的研究多集中于大跨越输电塔塔线耦合动力模型的研究;对电视塔和其它类型高耸结构的研究也仅针对顺风向采用常用的Davenport谱进行频域分析或采用风荷载模拟技术进行时程分析而得到结构在风荷载作用下的动力反应[5,6]。上世纪90年代以后随着风洞试验技术在实际工程中的大量应用,风洞试验日益成为结构设计的一个重要工具,一般适用于高层、超高层、复杂体型、大跨、高耸等结构[7~9]。而对于一些较小的结构,如图1所示的移动天线等,通常的做法是直接在结构被测点位置贴应变片、传感器来获得有限的振动信号,例如观测点的速度、加速度以及风速信号等,利用这种方法分析结构的动力反应存在以下几个困难:(1)现场作用于结构上的荷载很难确定,特别是脉动风荷载;(2)对结构的风荷载反应,包括构件的内力、连接件的内力进行实测有时存在较大难度;(3)由于脉动风荷载不能有效从现场实测中获得,而依据《荷载设计规范》也难以得到动力荷载时程,所以导致常规的有限元数值分析方法难以应用。
针对中国移动TD-SCDMA的第三代移动通信标准(简称3G)天线面板进行研究,如图1所示。

图1 6 m高的3G天线杆结构图Fig.1 Structural diagram of 3G antenna of 6m high

图2 现场试验测点布置图Fig.2 The layout of measuring points
这种天线杆结构一般都安装在城市高楼的顶端,因此对风荷载作用比较敏感,一旦在风荷载作用下失效,将会对通讯产生很大的影响。为了评估这些天线在风荷载作用下的动力反应,需要获得结构的各种力学指标,包括位移、应力、应变、轴力、弯矩等等。由于通讯的特殊性,这些天线一旦固定就不能随意拆卸,所以利用通常的做法很难完成。本文提出了一种现场实测的有限振动信号与结构有限元模型模拟分析相结合的方法来获得结构在实际风荷载作用下的动力反应全过程,可以得到结构内力,连接件内力,天线面板的加速度反应等全面的动力反应信息,也可以得到风荷载时程的定量估计。
1 风荷载作用下结构振动现场检测试验
首先采用环境激振的方法,用加速度传感器拾取仪进行数据采集及分析,最后得到天线抱杆平行天线平板方面和垂直天线平板方向的自振频率和风振响应。
在数据分析过程中利用仪器所记录的结构反应加速度信号来确定结构的参数和动力特性,这样处理问题的好处是:第一符合真实的情况,第二可以提高信号处理中的信噪比,第三省时、省力,并且减少了工作量。
用数据信号分析仪,首先将所记录的模拟信号数字化,然后计算出信号的自谱、互谱、传递函数和相干函数等。
现场试验中采用了表1所示的传感器及放大记录设备。

表1 试验中采用的仪器Tab.1 Apparatus used in experiment
测点布置在桅杆顶端,测试方向为垂直天线平面和平行天线平 面,如 图 2所示。

图3 南北向加速度时程曲线Fig.3 Acceleration time history(NS)

图4 南北向频谱曲线Fig.4 Frequency spectrum curve(NS)

图5 东西向加速度时程曲线Fig.5 Acceleration time history(EW)

图6 东西向频谱曲线Fig.6 Frequency spectrum curve(EW)
图3~图6为部分现场测试得到的结构加速度时程曲线及其频谱曲线,现场实测风速为:7.8m/s。通过现场实测,该天线桅杆相对较高,桅杆刚度相对较小,从频谱图上可以得到该天线系统的基本自振频率约为3.313 Hz,二阶自振频率约为3.563 Hz,在风速为4 m/s至12 m/s范围内桅杆顶点位移约为8 mm~10 mm。
2 脉动风的模拟计算
2.1 有限元模型的建立
利用ANSYS建立天线结构的有限元模型,如图7所示,模型的参数取值参见文献[10]。
为了更好地研究风荷载作用下天线的工作状况,对天线系统进行模态分析,由于各阶模态中只有前几阶模态对振动起决定性作用,故取前8阶的自振周期和自振频率,如表2所示。

图7 6 m高三叉杆天线系统有限元模型Fig.7 Finite element model of tripodal antenna system of 6m high

表2 前8阶自振周期和自振频率Tab.2 Natural vibration period and natural frequency of eighth order
从上表可以看出:一阶振型自振频率f=3.837 9 Hz,二阶f=4.009 3 Hz,三阶f=21.742 Hz,三阶与二阶和一阶相差较大,说明结构的响应主要以1,2阶振型为主,这与结构的形式有关,从试验测得的频谱图中也可以看出。
由于在建立有限元模型时做了一些简化处理,如:原结构天线面板与抱杆是靠联接件连接,而模型中只用了2根刚接杆代替,这样势必忽略了结构联结件与面板之间的摩擦力等因素,造成有限元模型与原结构存在一定误差,如果要提高计算精度,可以对模型做进一步优化,使其更符合原型,其次,试验过程中也存在一定误差。从计算结果看,简化的模型与现场实测的结果基本吻合,故该有限元模型可以用于模拟实际的天线结构系统。
2.2 脉动风荷载模拟的理论依据
对于顺风向,风荷载由两部分组成,一个是长周期分量的平均风,可以视为静荷载作用在结构上,另一部分是短周期分量的脉动风,可以视为时间t的一个随机过程。
对于脉动风,其强度是随时间t随机变化的,由于它的周期较短,其作用性质是动态的,因而应按动力反应来分析,本文采用多自由度体系来模拟脉动风荷载。
天线系统在风荷载作用下的运动方程为:

其中{P}为作用在天线面板上的实际风荷载,它是位置向量d(x,y)和时间f(t)的函数,由于天线面板面积较小,故假设风荷载压强在面板上每个点的分布均匀,由此可以得出风荷载只是时间t的函数。
将位移{u(t)}按振型展开,即作正则坐标变换:

将式(2)代入式(1)得:

前乘[φ]T,得到:
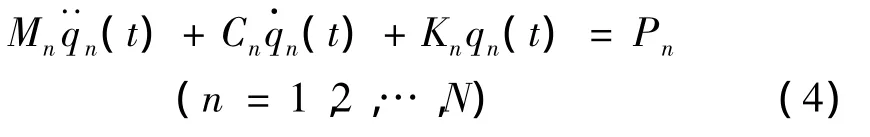
Mn、Cn、Kn、Pn分别为振型质量、正则阻尼系数、振型刚度和振型荷载。
对于风荷载作用下天线系统的振动,由于结构较柔,在脉动风作用下,一阶振型的振动占主要部分,因此可以采用一阶振型运动方程来简化模型,其一阶振型坐标运动方程为:

其中M1为一阶振型质量,C1为一阶振型阻尼,K1为一阶振型刚度,q1为振型坐标,P1为一阶振型对应的振型荷载。
两边同时除以振型质量M1,并根据K1/M1=,上式可简化为:

其中ω1为天线一阶自振频率,对于式(6),通过现场实测可以得到天线系统中具有代表性的一点,即桅杆顶端的一阶加速度时程曲线(t),利用下式变换:

可以分别得到体系中桅杆顶端的速度和位移时程曲线,如式(7)、式(8)所示,而ω1可由有限元模态分析获得,忽略阻尼的影响,将式(8)和ω1带入方程(6)中即可得到作用于天线面板上的模拟风荷载时程函数P1(t)/M1。显而易见,P1(t)/M1与实际的风荷载相差一个系数k。
为了求系数k,首先将已经得到的模拟风荷载P1(t)/M1施加到上面的有限元模型中,通过计算可以得到P1(t)/M1作用下结构顶点的位移时程曲线u1(t),对u1(t)做如下变换:

通过上面修正系数的方法可以得到与实测加速度时程相匹配的风荷载时程,同时也可以计算出天线连接件的内力反应时程。
2.3 未修正的脉动风荷载模拟结果




为验证本文所提方法的可行性和精度,通过现场实测,可以得到不同测试工况下天线的加速度时程曲线,为了使问题更加具有代表性,本文选取两条曲线(工况1和工况2),其中工况1的风速为7.8 m/s,工况2 的风速为 7.2 m/s。
以工况2为例,可以得到模拟的风荷载时程曲线P1(t)/M1,如图8所示,将该时程曲线施加到有限元模型中即可得到结构的加速度时程如图9所示。
其中加速度峰值为0.067 m/s2,而试验中实测的加速度时程如图12(a)所示,加速度峰值为1.96 m/s2,中间相差的系数k为29.3,将此系数乘以模拟的风荷载时程曲线P1(t)/M1即可得到实际风速条件下的风荷载时程曲线,再将修正后的风荷载时程曲线施加到有限元模型中,进而求得结构的动力反应,如轴力、剪力等。
2.4 修正后的脉动风荷载模拟结果
图10~图13分别为实测的和有限元计算得出的加速度和位移时程曲线,通过加速度和位移时程曲线对比可以看出,模拟结果与实测结果十分接近。
同时也可以得到天线系统在脉动风荷载作用下连接件轴向力的动力反应时程曲线,如图14所示。



3 结论
本文提出的结构动力反应分析方法不但减少了试验的工作量,没有影响到天线的正常工作,而且克服了脉动风荷载作用下结构现场检测试验方法存在的困难,从另一个角度提出了一种全新的简便方法来模拟风荷载,即结合现场实测的有限振动信号与结构有限元模型模拟分析的方法而获得结构在脉动风荷载作用下的内力,该方法需要首先测试结构在脉动风荷载作用下的有限振动信号,如:加速度时程和频谱曲线等,然后通过结构运动方程模拟出脉动风荷载时程并施加到结构有限元模型中,通过有限元计算求出模拟风荷载与实际风荷载之间的修正系数,最后把修正后的风荷载时程再次施加到有限元模型中从而得出结构在实际脉动风荷载作用下的内力。通过比较,有限元分析结果与实验结果吻合较好,该方法可以推广应用于其他类似的工程结构中。
[1]禹 慧.复杂高耸结构风洞试验及风振响应研究[D].上海:同济大学,2007.
[2]顾 明,叶 丰.典型超高层建筑风荷载频域特性研究[J].建筑结构学报,2006,27(l):30-36.
[3]顾 明,叶 丰.高层建筑风致响应和等效静力风荷载的特征[J].工程力学,2006,23(7):93-98.
[4]顾 明,叶 丰.高层建筑风致响应的简化分析方法[J].工程力学,2006,23(8):57-62.
[5]陈 波,瞿伟廉.高耸电视塔的动力特性及风振反应分析[J].武汉理工大学学报,2004,26(2):23-26.
[6]Cermak JE. Wind-tunneldevelopmentand trendsin applications to civil engineering[J].Journal of Wind Engineering and Industrial Aerodynamies, 2003,91:355-370.
[7]Kasperski M.Specification of the design wind load based on wind tunnel experiments[J].Journal of Wind Engineering and Industrial Aerodynamies,2003,91:527-541.
[8]楼文娟,孙 斌,卢 旦,等.复杂型体悬挑屋盖风荷载风洞试验与数值模拟[J].建筑结构学报,2008,28(1):107-112.
[9]许 伟,黄启明,李庆祥,等.大跨度结构风荷载的风洞试验和CFD数值模拟研究[J].工业建筑,2009,39(增刊):394-401.
[10]刘晶波,王宗纲,费毕刚,等.中国移动TD-SCDMA天线安全性评估检测计算分析咨询报告[R].2009.
