基于Gabor重构的发动机振声信号阶次分量瞬时幅值的提取

金 阳，郝志勇，郑 旭，景国玺

(1.浙江大学 能源工程学系，杭州 310027;2.湖北汽车工业学院 汽车工程系，十堰 442002)

往复运动的内燃机其确定性激励与其转速间存在固有的联系，激励频率与转频成倍数关系。内燃机在工作转速范围内加减速类似于给它自身施加了一种天然的扫频激励，只不过每个时刻的激励频率不是一个，而是多个成倍数关系的频率。与此过程同步测量的振动或噪声信号中必然包含了系统的动力学特性和声辐射特征，并且还是结构设计者所关心的工作频率内的特性。因而对变速阶段信号的特征提取具有工程应用意义［1］。

变速阶段的振声信号是非稳态的，在旋转机械领域，由于其信号中具有上述的以转速为基频的谐波性质，每个谐波称为阶次，因而对这类特定信号的分析也被称为阶次分析。已发展出数种相关的处理方法［2］，各有利裨及其适用场合。本文研究的是两种不需要角度域重采样的阶次分析技术-STFT与Gabor阶次跟踪［2-5］-两个方面的问题:

(1)STFT幅值谱及Gabor系数谱对阶次分量的分隔能力与什么有关?能否找出一个工程上可用的定量的评判标准?

(2)这两种技术在阶次分量瞬时幅值估计上的误差水平如何?

1 高斯窗STFT幅值谱的对阶次分量的分隔能力与阶次切片的幅值误差

1.1 离散STFT幅值谱

与FT谐波分析一样，对于离散信号s［i］，当采用的窗函数为 γ［i］时的离散 STFT 幅值{Am，n}m，n∈Z也采用类似的幅值校正算法:

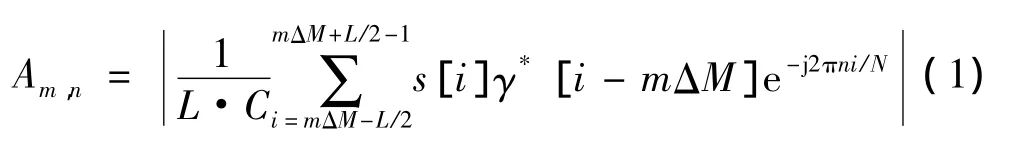
1.2 高斯窗

为了考查STFT幅值谱对阶次分量的分隔能力与窗参数的定量关系，除了选用时频集中性最好的高斯窗外，还将连续时间域高斯窗的时间标准差σi(s)(以下将简称为“窗宽”，它是时间信号持续时间的一种度量。)做为输入参数来生成STFT数值计算中的离散窗。这样做的好处是，我们研究的信号原本就是属于连续时间域上的，在同一域内便于发现变换结果与窗之间的联系。

设采样频率为fs(Hz)，离散点数为L(偶数)，窗序列的编号为i，则连续时间域中时间标准差为σt(s)的高斯窗函数离散后成为:

其中:

在数值计算中，L的选取应保证σN足够小。本研究的数值计算中，一般均保证σN≤0.1，这意味着在高斯窗的两端点的值已降至低于窗的峰值的0.2%。连续时间域中时间标准差为σt(s)的高斯窗函数的频域标准差(Hz)为:

1.3 仿真分析

构造的仿真信号为:

这是一个具有5个阶次分量并添加了白噪声的的信号(信噪比34 dB)，转速:n=60 t;第p阶分量的瞬时幅值:Ap(t)=1;而瞬时频率:fp(t)=p·t。对其采用不同σt的高斯窗进行离散STFT，生成峰值幅值谱以进行对比。图1是其中的3个结果。

每个结果中的图形区由上下两幅图组成:下方是时变单边峰值幅值谱，横坐标为时间(s)，纵坐标为频率(Hz)，颜色值为幅值(‘pk’代表峰值之意)。为解释上的方便，其中有标记为“0”与“1”的辅助点及一些辅助线;上方是“阶次切片”，是STFT单边峰值幅值谱上某阶次在不同时刻的理论瞬时频率处的对应值，横坐标为时间，纵坐标为幅值。

图1 信号S1在不同窗宽下的STFT单边峰值幅值谱(L:窗的点数;△M:以点数表示STFT的时间步长)Fig.1 STFT single-sided peak-amplitude spectra with different window width for signal S1(L:window length in point number，△M:time step in point number)

1.3.1 高斯窗STFT幅值谱的对阶次分量的分隔能力

STFT是最早使用的非稳态信号时-频分析方法，它的思想是直接而有效的。但其固有的局限性是时频分辨率不能同时提高。此仿真的目的不为了展示时间分辨率与频率分辨率之间反向变化的关系，而是想揭示在什么条件下，从STFT幅值谱上可以将各分量分隔开来，在分量间没有或较少有干扰现象。

信号分量的理论分布在时频面上越靠近的区域，在STFT频谱图上相应的区间，两分量间越易产生干扰模糊现象从而使分量难以分辨。变速阶段信号的特点是不仅同一时刻存在多个阶次分量，同一频率下也有多个分量。

为便于观察STFT对阶次分量的分隔能力与窗参数间的关系，图1中除了给出了σt、L、ΔM等分析参数的值外，还给出了6σf、6σt这两个值。

图1(a)中，辅助点“0”处的时刻为 6.82 s，在此处，相邻两阶次分量间的频率间隔均为6.82 Hz，等于6σf。在大于6.82 s的时段，所有相邻两分量之间没有明显的干扰现象，而在此时段不存在同一理论瞬时频率下的两相邻阶次分量间的时间间隔小于6σt的情况。

当 σt等于 200 ms，而 6σf等于 2.387 Hz时(图 1(b)):在大于2.387 s的时段，相邻阶次分量在同一时刻的理论频率间隔均大于6σf，但与图1(a)不同的是，在此时段却有干扰现象存在。4阶分量与5阶分量间的干扰出现在大约24 Hz以下;在24 Hz处，4阶分量对应的时刻是6 s，5 阶是4.8 s，两者间的间隔是1.2 s，等于6σt。同样，3阶分量与4阶分量间的干扰出现在大约14.4 Hz以下;而在该频率处3阶分量对应的时刻是 4.8 s，4 阶是3.6 s，两者间的间隔仍然是1.2 s，等于6σt。对图1(c)也有相同的观察，即虚假成分会出现在同一瞬时频率下时间间隔小于6σt的两分量之间。

综上所述，窗宽为σt的高斯窗STFT幅值谱如果可以将阶次分量区分开(各分量在时频谱上占据着互不重叠的区间)，且用fspacing，min(Hz)表示信号中所关心的时频范围内同一时刻分量间的最小理论频率间隔，而用tspacing，min(s)表示同一理论瞬时频率下的最小时间间隔，则σt应满足式(6):

式(6)等价于式(7):

这一现象可以从理论上进行定性的解释:高斯窗函数自身的 FT的主瓣在3σf处的值是其峰值的0.105，衰减 -19.5 dB，因此当同一时刻两分量的理论频率间隔大于6σf时，信号的理论频谱与窗频谱卷积后，两个分量所分布的主瓣之间交叠部分很少甚至没有，因而使它们得以区分。同样地，在时域中，当同一理论瞬时频率下两分量的时间间隔大于6σt时，这两个分量要么不能同时处于STFT过程中的移动窗内，即使都在一个窗内，也是分布在时域窗的趋于零值的两端，出现在STFT频谱上两者间干扰成分的量值就会很微弱。

在相邻阶次分量的阶次差相同的情况下，转速越低的时刻，越易违背式(7)中的最小频率间隔限值条件;转速越低、阶次越高的区域，相邻阶次分量同一理论瞬时频率间的时间间隔越小，越易违背式(7)中的最小时间间隔限值条件。

图2 线性变速段信号中阶次分量的理论时频位置示意图Fig.2 Schematic diagram for the theoretical time-frequency locations of the order components in a vibroacoustic signal with linearly varying speed

由图2可确定

1.3.2 高斯窗STFT幅值谱幅值误差

下面对于STFT幅值谱上能区分开阶次分量的地方，再来考察其阶次幅值的精度。从图1(a)、图1(b)、图1(c)中的阶次切片来看，这些值不宜做为阶次分量瞬时幅值的估计，甚至也不能做为瞬时幅值的相对大小的估计(见图1(b)与图1(c)，虽然各阶次理论瞬时幅值都为1，但STFT幅值谱上的各阶次理论频率处的值却不同)。非稳态信号的STFT幅值谱除了与窗有关，还与信号中分量的自身特征(瞬时幅值变化率、瞬时频率变化率)密切相关。从图1可知，分量在STFT幅值谱中所占据的频率宽度受窗宽与分量自身特征的共同决定;同一阶次分量的幅值误差随宽窗的增加而增加;同一窗宽下瞬时频率变化率越大的分量，其STFT幅值误差就越大。

2 基于Gabor阶次跟踪的阶次分量瞬时幅值估计

Gabor阶次跟踪是基于离散Gabor变换与展开这一变换对进行阶次分量时域重构的技术［6］。式(9)与式(10)分别是离散Gabor变换与展开式。

其中，M是Gabor变换的时间采样点数;N是频率分析点数;L是离散窗的点数;ΔM是以点数表示的时间步长。Gabor变换中的窗γ［i］被称为分析窗，而Gabor展开中的窗h［i］被称为合成窗。这一变换对存在的条件是h［i］与 γ［i］互为对偶函数(它们在式(9)与式(10)中的位置可以互换)，且过采样率ros需满足:

2.1 Gabor阶次波形重构的前提条件

如果对于一个离散分析窗，能够计算出其对偶窗，则用式(9)与式(10)总能实现采样信号的完全重构，无论这两个窗的时频集中性的相似程度如何。但若想实现信号中的特定分量的重构，还需要满足如下的要求:

(2)系数谱中与想提取出波形的分量有关的系数所占据的区域与其它分量间无重叠。前面的仿真分析已表明系数谱对分量的区分能力由信号中分量特点与分析窗共同决定;文献［3］中指出了Gabor阶次跟踪方法适用于“信号各阶阶比成分在时频面上可以和其它阶比成分分开时”，但并没有指出在什么条件下可以使它们分开，而本文的第一部分回答了这个问题。

(3)合成窗应具有与分析窗尽可能相同的时频集中性。由于Gabor基本函数通常并不构成正交基，所以其对偶函数不是唯一的。只有寻求到与分析窗的时频集中性最相近的对偶窗，当将m，n中与某分量对应的系数保留而其它位置处的值置为0(这一过程称为“时频遮罩”，有关“时频遮罩”的具体步骤可参见文献［3］)得到矩阵，n，并用如下公式:

进行重构所得到的波形才是与理论分量波形相近的。基于对偶窗函数之间的最小均方误差(LMSE)意义上的相似性，已发展出了似正交的 Gabor展开算法［7］。研究表明，对偶窗之间的相似性与过采样率有关，总的来说，过采样率越大，相似性越高。在给定的离散时间步长ΔM，频率区间点N下的高斯窗，其对偶窗与其具有最小均方误差时，该高斯窗的离散域时间方差为［8］:

由此，可推出对应的最佳连续时间域上的方差为:

2.2 改进的Gabor阶次分量重构流程

图3是常规的Gabor阶次波形重构流程，它以高斯窗作为合成窗，而不是分析窗。在此过程中，要获得区分得开阶次分量的Gabor系数谱，是通过窗参数的试凑来实现的，没有结合信号的特征，试凑的参数不一定能满足将相邻阶次分量区分开的条件。

图3 常规的阶次波形重构流程图Fig.3 The flowchart for the conventional order waveform reconstruction

基于本文中第1部分的仿真结论，提出一种改进的阶次波形重构算法，并对重构出的波形用Hilbert变换求包络作为阶次分量瞬时幅值的估计，全部流程如图4所示。

图4 基于改进的阶次波形重构算法的阶次瞬时幅值估计流程图Fig.4 The flowchart for the order component's instantaneous amplitude estimate based on the improved order waveform reconstruction algorithm

3 仿真验证与应用实例

为验证此流程对变幅值阶次分量的适用性，构造了如下的仿真信号:

对此信号，如果想提取800 r/min以上的30阶以内的阶次分量的瞬时幅值，按图4所示流程，求得fspacing，min是 285.6 ms，fspacing，min是 13.3 Hz，而可用的 σt的范围是35.8 ms～47.6 ms。

图5是σt=40 ms时的分析结果。图5(a)中的系数谱中30阶以下的阶次间没有出现干扰现象;采用对重构的阶次波形用Hilbert变换求包络做为瞬时幅值估计，其各阶误差在5%以内，而用STFT单边峰值幅值谱做为瞬时幅值估计，其误差会受阶次值影响，阶次越高，误差越大。

图5 仿真信号S2基于改进的Gabor重构流程的阶次瞬时幅值估计结果Fig.5 Result of the instantaneous amplitude estimates of the order components in signal S2 based on the improved Gabor reconstruction

仿真试验还表明，按图4所示流程、选用35.8 ms～47.6 ms之间的任何一值做为窗宽得到的阶次瞬时幅值估计都有与图5(e)中一致的误差水平，而STFT幅值谱做为瞬时幅值估计，窗宽越大，误差越大。

对将式(15)中的SNR改为5(14 dB)的仿真信号也按图4所示的流程做了仿真实验，此时得到的瞬时幅值相比于小噪声情况下的高频噪声要大，对该瞬时幅值进行小波降噪后再做为瞬时幅值估计，得到的各阶幅值误差在10%以内。

图6 某实测信号基于改进的Gabor重构流程的阶次瞬时幅值估计结果Fig.6 Result of the instantaneous amplitude estimates of the order components in a real-world signal based on improved Gabor reconstruction flowchart

图6是一个应用实例。试验发动机为某直列4缸高压共轭柴油机，标定工况为82 kW/(3 600 r/min)，在一电控电涡流测功机上进行全负荷加速试验。发动机从900 r/min线性加速到3 600 r/min，用时30 s，用B＆K公司数采设备同步测量振声信号。图6(b)中的信号为距离机体ATS侧中心1 m处的声压。对该信号进行阶次分析的参数是:相邻阶次分量的阶次差:Δp=0.5;最大分析阶次:pmax=10;转速范围:1 000 r/min～3 400 r/min(图中只显示了一部分)。图6(a)是其Gabor系数谱，从中可见，主要能量集中在偶数阶阶次上，这与直列4缸机的不平衡的2阶往复惯性力及各缸激励转矩合成后的主要阶次为偶数阶的特点是一致的。根据转速与时间的对应关系，从图6(d)转换成图6(e)的图形对于定位噪声大的转速、噪声源识别、声学仿真模型的验证及零部件改进设计都有指导作用。

4 结论

(1)提出了工程上可用的高斯窗时间标准差与STFT幅值谱/Gabor系数谱对阶次分量分隔能力之间的定量关系式。仿真与实际应用证明了此关系式的适用性。

(2)虽然与FT谐波分析一样采用了幅值校正，但STFT幅值不能做为瞬时幅值估计，其误差水平会因阶次、转速变化率、窗宽而不同。

(3)采用文中提出的改进的阶次波形重构算法进行瞬时幅值估计的优点是:①能判定是否存在对所关注的阶次分量进行理想重构的高斯窗时间标准差(见图4中的判断分支);②在存在适合窗宽的情况下，在小噪声情况下，可直接用重构的阶次波形的包络做为瞬时幅值估计;大噪声情况下，还需对该包络进行降噪处理，以保证阶次分量瞬时幅值估计的精度。

［1］赵晓平，张令弥，郭勤涛.旋转机械阶比跟踪技术研究进展综述［J］.地震工程与工程振动，2008，28(6):213-219.

［2］孔庆鹏，宋开臣，陈 鹰.发动机变速阶段振动信号时频分析阶比跟踪研究［J］.振动工程学报，2005，18(4):448-452.

［3］郭 瑜，秦树人.基于瞬时频率估计及时频滤波的阶比分量提取［J］.中国机械工程，2003，14(17):506-1509.

［4］田 昊，唐力伟，田 广，等.基于核独立分量分析的齿轮箱故障诊断［J］.振动与冲击，2009，28(5):163-164.

［5］ Qian S.Gabor expansion for order tracking［J］.Sound and Vibration，2003，37(6):18-22.

［6］Shao H，Jin W，Qian S.Order tracking by discrete Gabor expansion［J］.IEEE Transactions on Instrumentation and Measurement，2003，52(3):754-761.

［7］ Qian S，Chen D.Discrete Gabor transform［J］.IEEE Trans.Signal Processing，1993，41(7):2429-2439.

［8］ Qian S.Introduction to time-frequency and wavelet transforms［M］.Upper Saddle River，NJ:Prentice Hall PTR，2002:41-72.