基于广义解调时频分析和瞬时频率计算的阶次谱方法在齿轮故障诊断中的应用
2011-02-13程军圣李宝庆
程军圣,李宝庆,杨 宇
(湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082)
齿轮在启停过程中,其振动信号包含了丰富的状态信息,一些在平稳运行时不容易反应出来的故障征兆有可能会充分地表现出来。在这个过程中,齿轮的振动信号为变速非平稳信号,而且表现为多分量的调幅-调频特征[1],采用传统方法无法从频谱分析中有效地提取故障特征[2]。考虑到齿轮启停过程中的振动信号表现出随转速变化的调频特征,可以采用阶次分析方法提取故障特征,该方法可以有效地提取随转速变化的振动信号的故障特征[3,4]。
当齿轮发生故障时,其振动信号的幅值和相位都会发生变换,产生幅值和相位调制,而相位的调制信息往往包含了齿轮的故障特征。在幅值调制方面,如包络解调等方法现在已经研究的比较成熟,文献[3]就是综合使用了包络分析方法和阶次分析方法;而在相位调制方面,相关的研究相对来讲比较少,本文针对齿轮故障振动信号的相位调制特点提出了基于瞬时频率计算的阶次谱方法,该方法首先计算信号的瞬时频率,然后对瞬时频率信号进行等角度重采样,再对重采样信号进行频谱分析得到阶次谱,从而提取故障特征,进行齿轮故障诊断。但是,齿轮发生故障时,其振动信号还表现为多分量的调幅-调频信号,在计算信号的瞬时频率之前还需要将其分解为若干个单分量的调幅-调频信号之和,因此,在启停过程中对齿轮进行故障诊断的关键就在于找到一种有效的多分量信号分解方法。目前,常用的方法有EMD(Empirical Mod Decomposition,简称 EMD)[5,6],该方法由于其自适应性而在多分量信号分解中得到了广泛应用,但是它在理论上还存在频率混淆、端点效应等问题[7,8],这些问题仍然处在研究当中。
广义解调时频分析方法[9]采用广义解调把时频分布是倾斜、非线性或曲线的调制信号变换为时频分布是线性和平行于时间轴的信号,然后对变换后的信号进行小波包分解,只要选择合适的小波包分解尺度和分解树结构,得到的小波分解结果就是瞬时频率和瞬时幅值都具有物理意义的单分量信号,进一步求出各个单分量信号的瞬时频率和瞬时幅值,从而实现对调制信号的解调。由广义解调时频分析方法得到的各个分量可以是调幅-调频的,因此该方法非常适用于处理多分量的调幅-调频信号。而当齿轮存在故障时,其启停过程中的振动信号表现为多分量的调幅-调频特征,因此广义解调时频分析方法是非常适合处理启停过程中的齿轮故障振动信号的。本文将广义解调时频分析方法引入齿轮故障诊断,提出了基于广义解调时频分析和瞬时频率计算的阶次谱方法,首先采用广义解调时频分析方法将齿轮瞬态信号分解为若干个单分量信号,然后计算各个分量的瞬时频率,再对其瞬时频率信号进行重采样,最后对重采样信号进行频谱分析得到阶次谱,从而提取齿轮振动信号的故障特征。仿真和实验信号的分析结果表明,基于广义解调时频分析和瞬时频率计算的阶次谱方法可以有效地应用于启停过程中的齿轮故障诊断。
1 基于广义解调时频分析和瞬时频率计算的阶次谱方法
广义解调时频分析方法的关键在于找到了一种信号变换方法,能把时频分布是倾斜、非线性或曲线的信号变换为时频分布是线性的平行于时间轴的信号,它实际上是广义傅里叶变换和小波变换的混合体。该方法综合运用了解析向量和广义解调的方法,采用小波包分解方法将广义解调后得到的解析信号分解为若干个分量之和,任何一个分量只包含在小波包时频空间的一个矩形时频块中,在小波包时频空间的任何一个矩形时频块中最多只包含一个分量,从而使得瞬时频率和瞬时幅值都具有了物理意义,再对各个分量进行逆广义解调后求出瞬时频率和瞬时幅值,进一步就可以得到原始信号完整的时频分布,即Hilbert谱或Hilbert能量谱,其具体步骤可参见文献[10]。
当齿轮发生故障时,其振动信号的幅值和相位同时发生变化,产生幅值和相位调制,忽略齿轮箱传递函数对齿轮振动信号的影响,传感器拾取的齿轮箱故障振动信号为[11,12]:

式中,Xm为第m阶啮合频率谐波分量的幅值,φm为第m阶啮合频率谐波分量的初相位,fs为轴的转频,z为齿轮的齿数;dm(t)和bm(t)分别是第m阶啮合频率谐波分量的幅值和相位调制函数。当齿轮出现局部故障时故障齿随轴每周啮合一次,因此dm(t)和bm(t)是以轴转频fs为重复频率的周期函数。进一步将式(1)写成如下形式
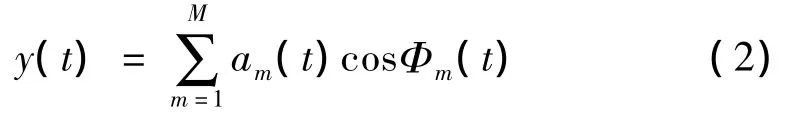
式中:am(t)=Xm[1+dm(t)],Φm(t)=2πmzfst+ φm+bm(t)
从式(2)中可以看出齿轮故障振动信号是典型的多分量调幅—调频信号,含有若干个啮合频率族,每一个啮合频率族am(t)cosΦm(t)又是一个单分量调幅—调频信号,因此为了提取信号的相位调制信息bm(t),可以首先采用广义解调时频分析方法对齿轮故障振动信号进行分解,将各个频率族分离得到若干个单分量信号,其中每个单分量信号代表齿轮振动信号的一个以某阶啮合频率mfz为中心的频率族或者为噪声分量。
为进一步研究齿轮振动信号相位调制特性,给出相位调制函数[13]:
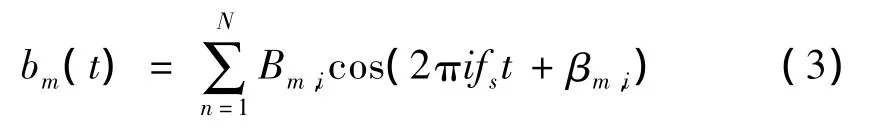
式中:Bm,n为调频指数;βm,n为其相位。
对于经过广义解调时频分析方法分解得到的每一个单分量信号可以给出其瞬时频率,即:
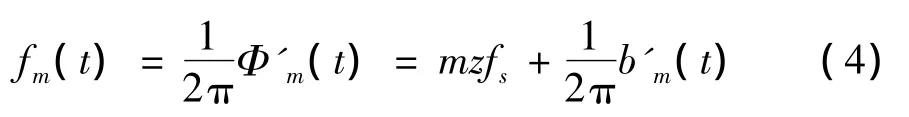
在齿轮启停过程中,转频fs是随时间变化的,因此式(4)中的b'm(t)也是随时间变化的函数。因此分解得到的各个分量的瞬时频率fm(t)是被转频fs调制以后的调制信号,也就是说各个分量的瞬时频率信号fm(t)是一个变调频信号,需要使用阶次分析方法来获得故障特征。我们可以先对齿轮启停过程中的振动信号的各个单分量的瞬时频率fm(t)进行等角度采样,得到等角度采样信号Fm(t),再对Fm(t)进行快速傅里叶变换。
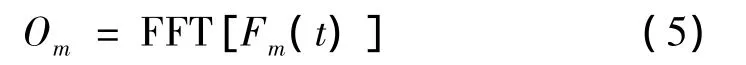
在对瞬时频率fm(t)等角度采样前我们需要首先计算各个单分量的瞬时频率,因此,式(5)定义为基于瞬时频率计算的阶次谱。
基于广义解调时频分析和瞬时频率计算的阶次谱方法步骤如下:
(1)根据齿轮转速信号r(t)估计相位函数s(t)。
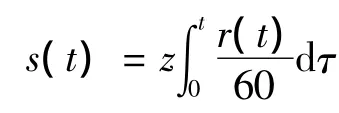
(2)采用文献[10]中提出的改进的广义解调时频分析方法对齿轮振动信号x(t)进行分析,得到若干个单分量信号 c1(t),c2(t),…,cN(t)。
(3)采用Hilbert变换计算各个单分量信号ci(t)的瞬时频率,得到瞬时频率信号fm,i(t)。
(4)对瞬时频率信号fm,i(t)进行等角度重采样,得到重采样信号Fm,i(t)。
(5)对重采样信号Fm,i(t)进行频谱分析,得到阶次谱。
2 应用
2.1 仿真信号分析
考察式(6)所示的多分量调幅-调频信号:
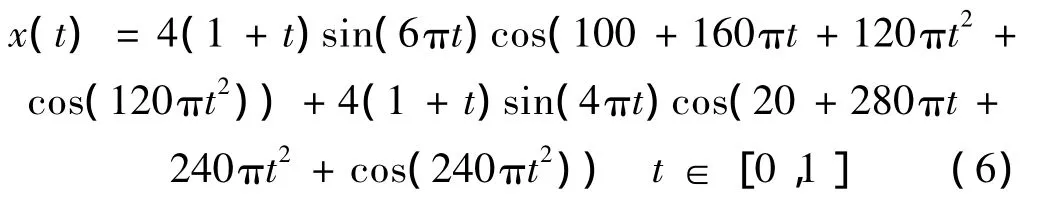
该信号及其两个分量x1(t)和x2(t)的时域波形如图1所示,采样频率为1 024 Hz。先直接采用MODWPT对仿真信号进行分析[13],近似地估计出相位函数s(t)=110t2,然后确定分解层数J=2,选择长度L=22的Fejer-Korovkin小波滤波器对仿真信号进行广义解调时频分析,得到的分解结果如图2所示。
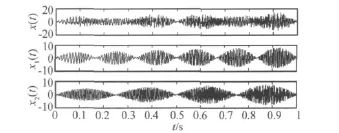
图1 仿真信号及其分量的时域图形Fig.1 The time waves of the simulated signal and its components
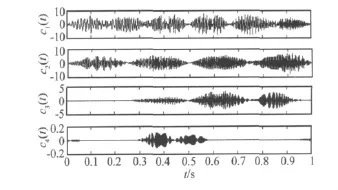
图2 仿真信号的广义解调时频分析分解结果Fig.2 The generalized demodulation time-frequency analysis results of the simulated signal
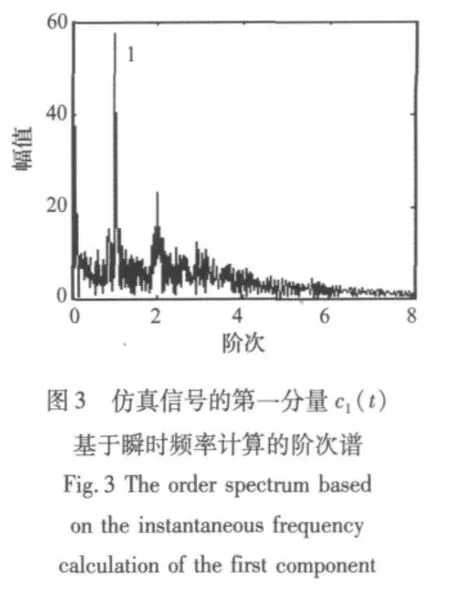
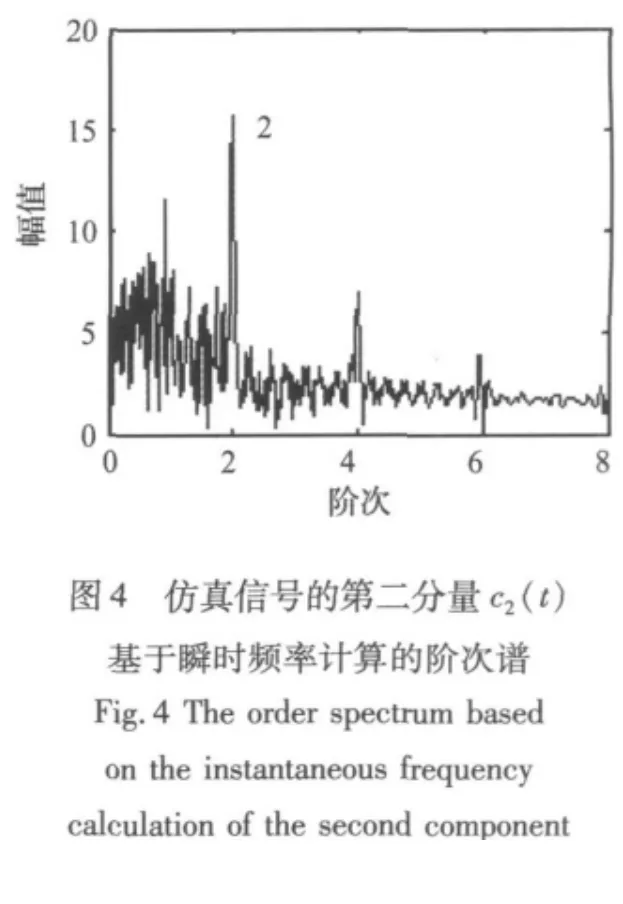
假设给出的仿真信号是某一转频fs(t)=120t的齿轮振动信号,对图2中的分量c1(t)、c2(t)采用 Hilbert变换计算其瞬时频率,再进行等角度采样,进行频谱分析后得到阶次谱,如图3和图4所示。从图3中可以看出,在阶次为1处有明显的峰值,从图4中可以看出,在阶次为2处有明显的峰值,说明两个分量信号被转频调制。因此,基于广义解调时频分析和瞬时频率计算的阶次谱方法可以有效地提取非平稳转速下相位调制信号的调制信息,可以有效地应用于非平稳转速下的齿轮故障诊断。
2.2 齿轮故障分析
图5 断齿齿轮的振动加速度信号Fig.5 The vibration accretion signal of the broken gear
为验证方法的有效性,在实验台上进行了正常、断齿齿轮两种工况的瞬态实验,采用模数为2 mm,齿数为55的两个标准直齿轮,齿轮转动轴上负载的转动惯量为 0.03 kg·m2。在齿轮箱上拾取加速度振动信号,通过光电式转速传感器拾取转速信号,采样频率为8 192 Hz。图5是断齿齿轮振动加速度信号的时域波形,其转速曲线如图6所示。
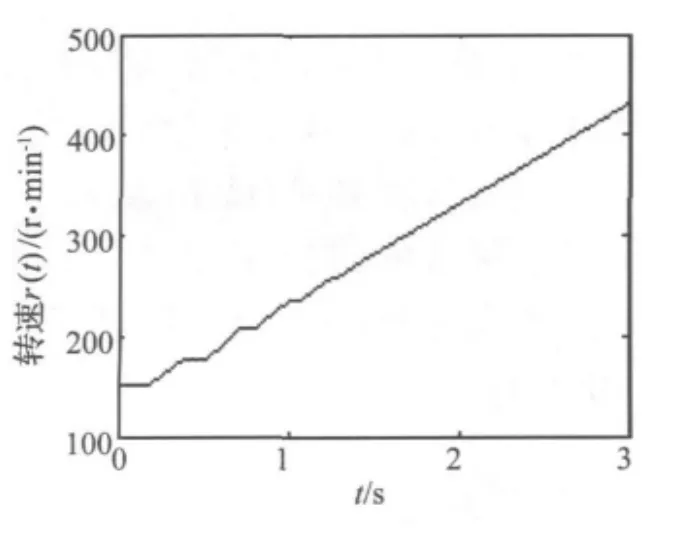
图6 断齿齿轮的转速信号Fig.6 The ration speed signal of the broken gear
对振动加速度信号直接进行基于瞬时频率计算的阶次谱分析,结果如图7所示,从图中可以看到,虽然存在与转频有关的阶次1,但是还含有幅值更高的与转频无关的阶次,其原因在于振动信号不仅是一个多分量的调幅—调频信号,其各个分量的瞬时频率随时间发生变化,而且还含有较强的噪声,从而导致振动信号故障特征不明显,因此直接对其分析无法判断齿轮的工作状态,需要对其做进一步处理。
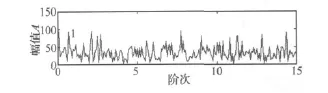
图7 断齿齿轮振动信号基于瞬时频率计算的阶次谱Fig.7 The order spectrum based on the instantaneous frequency calculation of the broken gear vibration signal
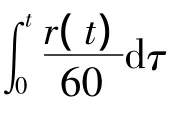
进一步对广义解调时频分析的各个分量使用基于瞬时频率计算的阶次分析方法进行分析,结果显示第1个分量c1(t)和第2个分量c2(t)的阶次谱(分别如图9和图10所示)在阶次为1处都有明显的最高峰值,对应着齿轮的转频,说明齿轮振动信号被转频成分幅值调制了,这正是齿轮出现断齿故障时振动信号的特征,与实际情况吻合。
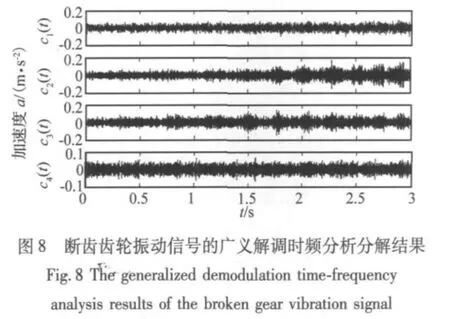
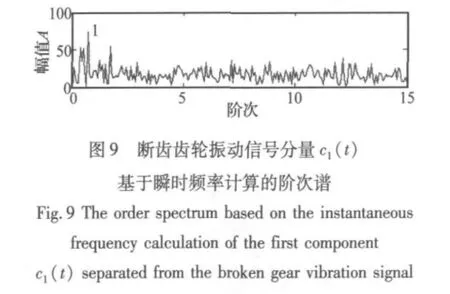
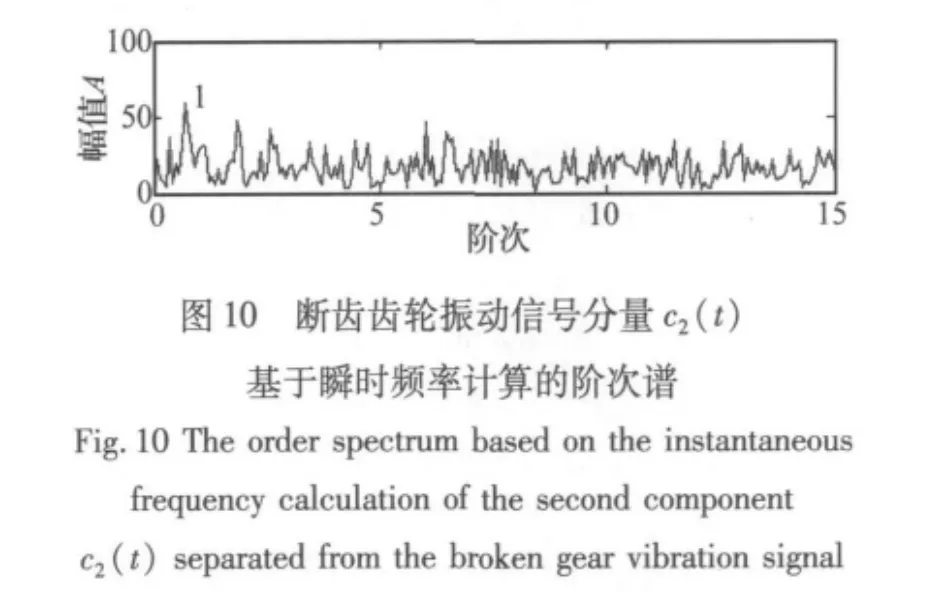
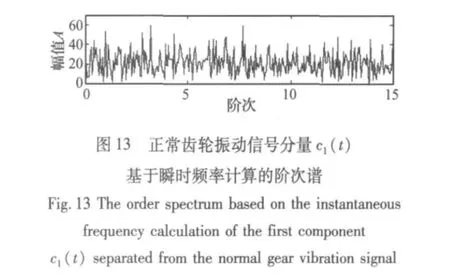
图11和图12分别是正常齿轮的振动加速度信号及其转速曲线,采用上述同样方法对齿轮振动加速度信号的各个分量进行分析,得到各个分量的阶次谱,分别如图13~图16所示,从这些图中都未能找到与转频有关的阶次。
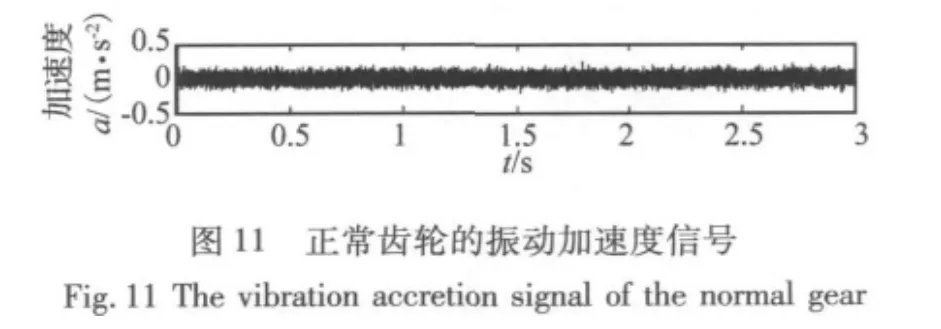
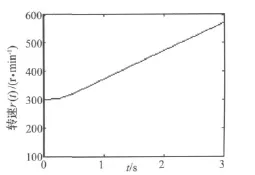
图12 正常齿轮的转速信号Fig.12 The ration speed signal of the normal gear

实验结果分析显示,基于广义解调时频分析和瞬时频率计算的阶次谱方法能够有效地提取齿轮故障特征,可以进行齿轮故障诊断。
3 结论
阶次分析的实质是将时域的非平稳信号通过等角度采样转换为角域的稳定信号,以便更好地反映与转速相关的信息。而当齿轮发生故障时,在启停过程中其振动信号表现为多分量的调幅—调频特征,因此为了提取故障信号的调频特征,一方面需要将多分量的调幅—调频信号进行分离,另一方面,对分离得到的单分量信号计算其瞬时频率后进行阶次分析。基于此,本文提出了基于广义解调时频分析和瞬时频率计算的阶次谱方法,采用广义解调时频分析方法将齿轮瞬态信号分解为若干个单分量信号,然后计算各个分量的瞬时频率,再对其瞬时频率信号进行重采样,最后对重采样信号进行频谱分析得到阶次谱,就可以提取与转频有关的调频特征,从而有效地进行故障诊断。值的提出的是,在采用本文所提出的方法时需要估计相位函数,这在实际应用中可能会有一定的困难,如何针对不同的实际问题估计相位函数还需要做进一步的研究。
[1] Ma J,Li C J.Gear defect detection through model based wideband demodulation of vibrations[J].Mechanical System and Signal Process,1996,10(5):653-665.
[2]康海英,栾军英,田 燕,等.阶次跟踪在齿轮磨损中的应用[J].振动与冲击,2006,25(4):112-118.
[3]康海英,栾军英,郑海起.基于阶次跟踪和经验模态分解的滚动轴承包络解调分析[J].机械工程学报,2007,43(8):119-122.
[4] Fyfe K R,Munck E D S.Analysis of computed order tracking[J].Mechanical Systems and Signal Processing,1997,11(2):187-205.
[5]Huang N E,Shen Z,Long S R.A new view of non-linear water waves:the Hilbert spectrum[J].Annu.Rev.Fluid Mech,1999,3l:4l7-457.
[6]Huang N E,Shen Z,Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.Lond.A,l998,454(1971):903-995.
[7]Lei Y,He Z,Zi Y Y.Application of the EEMD method to rotor fault diagnosis[J].Mechanical Systems and Signal Processing,2009,23:1327-1338.
[8]Qi K Y,He Z,Zi Y Y.Cosine window-based boundary processing method for EMD and its application in rubbing faultdiagnosis[J]. MechanicalSystems and Signal Processing,2007,21(7):2750-2760.
[9] Olhede S,Walden A T.A generalized demodulation approach to time-frequency projections for multi-component signals[J].Proceedings of the Royal Society A,2005,461(2059):2159-2l79.
[10]程军圣,杨 宇,于德介.基于广义解调时频分析的多分量信号分解方法[J].振动工程学报,2007,20(6):563-569.
[11] McFadden P D.Examination of a technique for the early detection of failure in gears by signal processing of the time domain average of the meshing vibration[J].Mechanical Systems and Signal Processing,1987,(1):173-183.
[12] Dalpiaz G,Ribola A,Rubini R.Effectiveness and sensitivity of vibration processing techniques for local fault detection in gears[J].Mechanical Systems and Signal Processing,2000,14(3):387-411.
[13] Olhede S,Walden A T.The Hilbert spectrum via wavelet projections[J].Proc.R.Soc.London.A,2004,460(2044):955-975.
