控制系统的脆弱性与鲁棒性

何朕， 饶丹， 王广雄， 刘志远

(哈尔滨工业大学航天学院，黑龙江哈尔滨 150001)

控制系统的脆弱性与鲁棒性

何朕， 饶丹， 王广雄， 刘志远

(哈尔滨工业大学航天学院，黑龙江哈尔滨 150001)

针对脆弱性有不同的理解，提出了一种新的关于脆弱性的概念。脆弱性是指一个优化设计的控制系统却失去了稳定裕度。文中对此进行了分析和说明，指出这脆弱性问题并不是因为控制器的脆弱性造成的，其根本的原因是在最优控制本身，是最优设计的手段或所用的判据造成的。因为H∞优化设计中并没有用到稳定裕度的概念。在多入多出系统的设计中由于用的是奇异值而不是各个物理变量，所以就有可能忽略了单个回路的鲁棒稳定性问题。这个新的脆弱性概念也不同于一般控制器参数摄动下的鲁棒性问题，将有助于理解一个设计良好的系统在实际调试中可能出现的稳定性问题，所以对理论和实践都有重要意义。文中附有设计分析的例子，其中的一个例子取自作者在实验中所遇到的问题。

脆弱性;鲁棒性;稳定裕度;H∞优化设计;球－杆系统

0 引言

脆弱性是近年来控制界经常提到的一个话题，但是理解却并不相同。脆弱性是指对控制系统进行优化设计却失去了鲁棒性，因而实际上无法稳定工作。文献［1］将此原因归结为控制器的脆弱性。但是脆弱性问题不是一个简单的控制器问题，所以文献［1］一经提出就遭到 Mkil的质疑［2］，并进一步专门著文来阐述其观点［3］。本文并不从控制器上来找原因，本文认为控制系统脆弱性的根源在于控制系统的设计理论本身。本文将从控制系统的优化设计，尤其是H∞优化设计的实质来对脆弱性问题进行分析，提出一种新的关于脆弱性的概念。

1 系统的脆弱性

脆弱性的概念是与现代的控制系统的优化设计相伴随而出现的［1］。现代的各种鲁棒设计理论都是与对象的某种不确定性联系在一起的。例如H∞设计中常用乘性不确定性来描述未建模动态，要求

式中lm(ω)为乘性不确定性的界函数，并称这个条件为鲁棒稳定性条件［4］。但这只是一种相对于乘性不确定性来说的稳定性条件。文献［5］则讨论了更为一般性的情形，如图1所示。这里的不确定性Δ是更为一般的2入2出的4块结构的不确定性，图中G为对象，K为控制器。对于图1的系统来说，设计指标是Tzw(jω)的H∞范数‖Tzw‖∞，式中Tzw是从w=[w1w2]T到z= [z1z2]T的闭环传递函数。‖Tzw‖是图1反馈系统的鲁棒稳定性的度量，文献［5］中将其定义为稳定裕度。总之，现在的各种鲁棒控制问题中的不等式条件，虽然反映了某种稳定问题，实际上都是相对于对象的某种不确定性来说的。这种鲁棒设计一般并不关注Nyquist稳定判据中的稳定裕度。虽然这些理论，例如 H∞控制本身可确保所设计系统的稳定性，但H∞设计并没有指定幅值裕度或相位裕度。如果这时这种稳定裕度非常小，那么所设计的系统实际上是不能工作的，这就是脆弱性的概念。

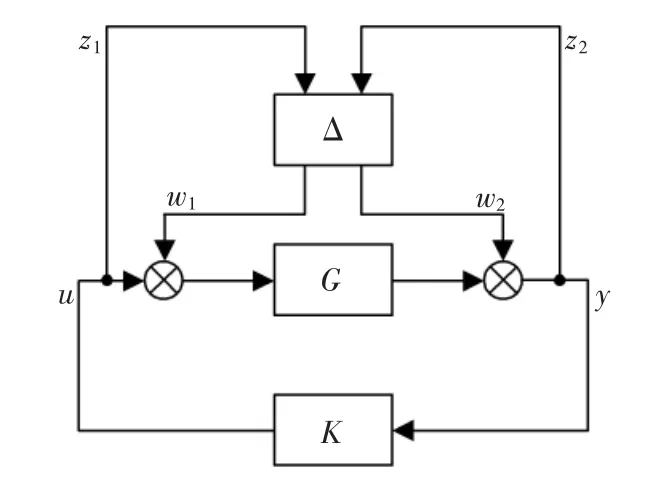
图1 2入2出的不确定性系统Fig.1 System with a 2×2 uncertainty

还有一种情况是，控制系统的鲁棒性是与所考虑问题中的结构形式有关的。例如最优控制的LQG问题，当从分离定理的角度来考虑时，最优控制的状态反馈具有很好的鲁棒性，但如果是从控制器加对象的角度来考虑时，就可能没有鲁棒性［4］。在MIMO系统的H∞优化设计中也会有类似的问题，例如当H∞范数或最大奇异值特性满足鲁棒设计要求时，从单个回路(对应每一个具体的输出变量)来分析时也可能缺少鲁棒性。如果这时的稳定裕度几近消失，就称这个设计是脆弱的。这也是一种脆弱性的概念。

因为上述的系统在设计时都已经满足了所定义的稳定条件，或者满足了小增益定理的不等式，如果再出现稳定性问题，有人就会将原因归结为控制器问题，文献［1］认为这是控制器的脆弱性引起的。但是控制器的脆弱性不同于上述没有鲁棒性的问题，所以文献［1］一经提出，就遭到 Mkil的质疑［2－3］。将这种失去稳定性的原因归结为控制器脆弱性的学派，是把这个问题看做是控制器参数摄动引起的鲁棒性问题，近年来关于脆弱性的文献大都持这种观点，其基本思想可参见文献［6］。而Mkil的观点则认为控制器脆弱性是指控制器参数的极微小摄动(例如由于字长有限而使系数出现误差)可能会导致控制器本身从稳定变成不稳定，并认为这不是常规的摄动的概念，也不是用常规的鲁棒理论可以解决的。Mkil认为控制器的脆弱性是一种控制律算法实现上的问题(包括系数的字长和算法灵敏度等)，而不是直接从状态方程式的系数上可以来讨论的问题［2］。本文认为上面提到的这种系统失去鲁棒性的问题并不是控制器本身的问题。所以这里不用控制器脆弱性这个概念，而是将这种鲁棒性问题称为控制系统的脆弱性。这里是将根据各种优化设计或鲁棒设计理论所得的系统，但缺乏(或几近消失)幅值裕度或相位裕度的系统，称为脆弱性系统。这种系统虽然在理论上或仿真验证时是满足设计要求的，但由于(控制器)实现时存在的各种可能的差异，因为没有稳定裕度而使系统实际上无法稳定工作。这个脆弱性问题是因为某些优化设计中缺乏(或无法)考虑到一些基本的稳定裕度，因而是不能用同一个理论框架来进行评估或避免的。脆弱性问题在经典理论时期是不存在的，只有在现代的各种优化设计和鲁棒设计中才有可能出现，所以在采用各种新的设计理论时，应该注意加以防范。

下面通过两个设计的例子来作进一步的说明。第一个例子取自H∞控制的一个最基本的概念:双互质分解。第二个例子则是作者为球－杆实验系统配置H∞控制器时所遇到的问题。

2 设计分析(1):双互质分解控制器

双互质分解是H∞控制理论中的一个最基本概念。根据对象的双互质分解，可以写出一个能使对象稳定的控制器的参数化公式。这样就消除了H∞控制中要求内稳定的约束条件，进而得到一个可以求解的模型匹配问题［7］。这里对采用双互质分解设计的控制系统进行分析，以便进一步了解H∞控制中所可能隐藏的脆弱性问题。

设对象

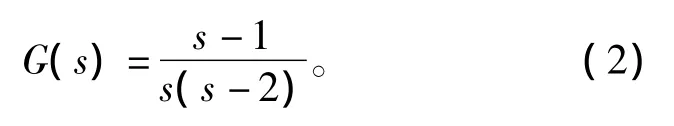
将G进行双互质分解，G=NM－1=珟M－1珟N，根据双互质分解中的X阵和Y阵，可得到控制器

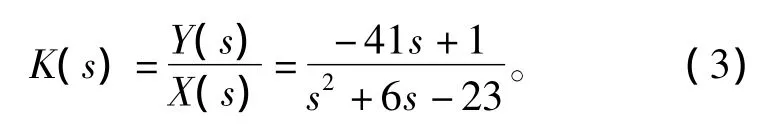
此例取自文献［7］，式中各符号的说明可参见该文献。

根据式(2)、式(3)可得此反馈系统的特征方程式为

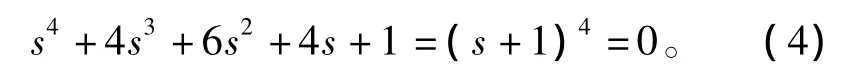
式(4)表明，该系统的4个极点都在－1点上，应该是具有很好的动态性能了。现在再从负反馈的角度来对此系统进行分析。系统的开环传递函数为

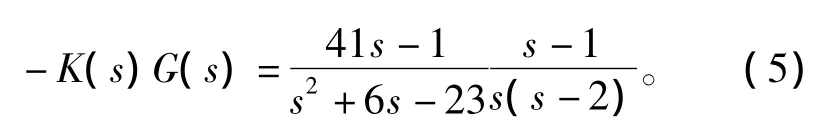
因为是从负反馈来考虑，所以要用－KG。图2所示就是此系统的Nyquist图。图2表明，虽然系统是稳定的，但Nyquist图线离－1点非常近，系统实际上没有鲁棒性，参数稍有摄动就不稳定了，这样的系统实际上是不能工作的。这种设计就称为是脆弱的。其实H∞优化设计确实有可能隐藏着脆弱性，文献［1］在提出脆弱性概念时就有两个脆弱性的例子是来自早期的H∞控制的经典著作［8］。

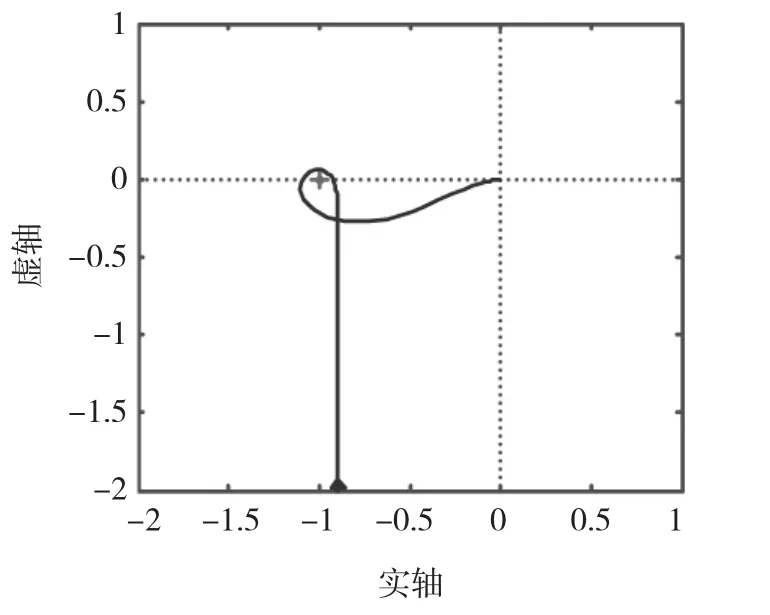
图2 基于双互质分解设计的Nyquist图Fig.2 Nyquist plot of a doubly-coprime factorizationbased design

3 设计分析(2):球－杆系统的H∞控制

图3是德国Amira公司生产的BW500球－杆实验系统，小球可以在杆上自由滚动，系统的控制输入是施加在杆上的力矩τ，通过杆的转动来控制球在杆上的位置。忽略一些次要的阻尼系数后，此球－杆系统的数学模型可写成［9］

式中:x1是球在杆上的位置，即图中的r;x2是球的移动速度;x3是杆的转角θ;x4是杆的转动速率。该实验系统原配有状态反馈［10］，作者利用 MATLAB的实时工作站(real time workshop，RTW)为实验系统设计了一个H∞控制器对此球－杆系统进行控制。由于利用了原实验系统的位移传感器(光学镜头)和转角传感器(码盘)，所以H∞设计中的对象是1入2出的。图4所示是H∞设计时的系统框图。这是H∞设计中的PS/T问题:

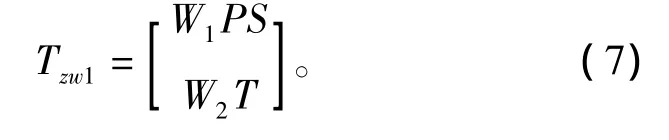
式中:W1是性能权函数;P是对象;S是对象输入端的灵敏度函数;W2是乘性不确定性的权函数(界函数);T是系统的闭环传递函数。Tzw1是从输入w1到输出z= [z1z2z3]T的传递函数。图中w2是因为H∞设计中秩的问题而附加的一个小信号。

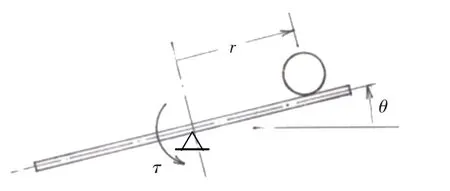
图3 球－杆系统Fig.3 Ball-and beam system

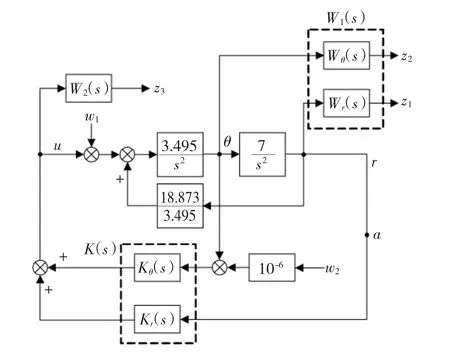
图4 H∞设计的框图Fig.4 Block diagram of the H∞ design

因为考虑到θ回路和r回路应该具有不同的带宽，故取性能权函数为

在式(9)、式 (10)的权函数下，利用 MATLAB的hinfsyn函数求解这个PS/T问题，得‖Tzw1‖∞=γ=0.997 0，对应的H∞控制器为(注:已略去104以上的高频分量)

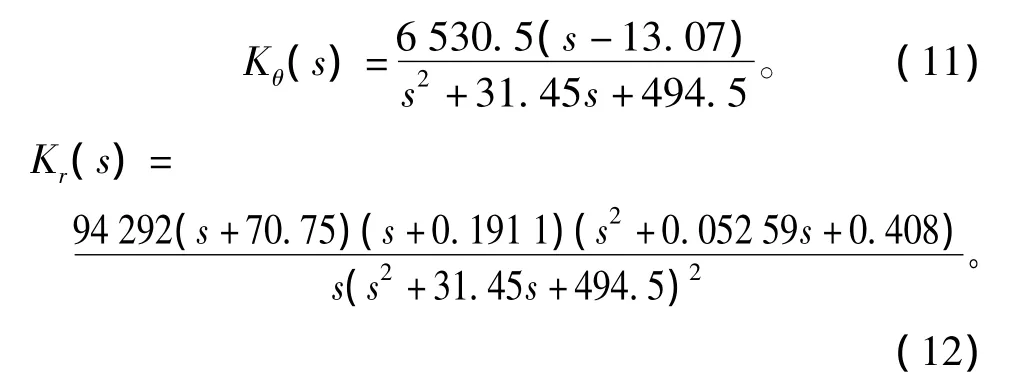
作为对H∞优化设计的验算，图5列出了式(7)中关于鲁棒稳定性的W2与T的相对关系图。对于性能的W1PS也可得类似的Bode图。对设计结果的时域仿真也表明本例的H∞设计是成功的。可是这个H∞控制器在RTW环境下实现后却无法使实际系统稳定下来。进一步的分析表明，是因为这个球－杆系统的H∞设计存在脆弱性。

虽然H∞设计是用奇异值来设计的，但具体实现时却是一个一个具体的物理变量与H∞控制器来连接的。现在就来分析这个用H∞设计好的系统的输出变量r(小球位置)的回路特性。具体做法是将图4在a点处断开，来考察这个回路的Nyquist特性。图6就是这个r回路的Nyquist图。从图6(b)可以看到，Nyquist图线与负实轴的交点为－1.04和－0.862，图中的相位裕度仅为2.46°(对应ω=4.83 rad/s)。这些幅值裕度和相位裕度的值都可以用仿真来进行验证(图略)。由于这个小球的位置(r)回路的相位裕度几近消失，所以实际上这个系统是无法稳定工作的。这也就是说，球－杆系统的这个PS/T问题的解，虽然满足了H∞鲁棒设计的要求，并且通过仿真验证，但却是脆弱的，在实际系统中是不能实现的。

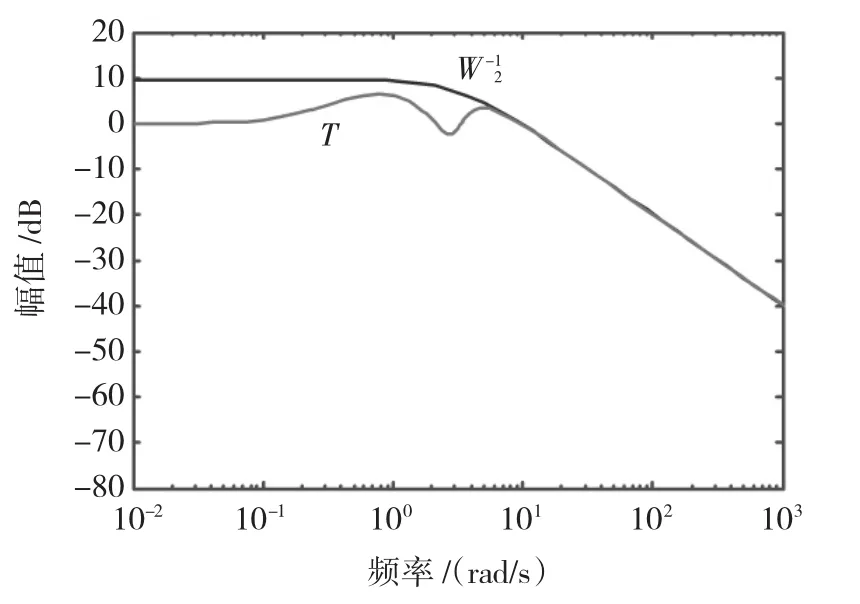
图5 补灵敏度T与的Bode图Fig.5 Bode plot of the complementary sensitivity T and

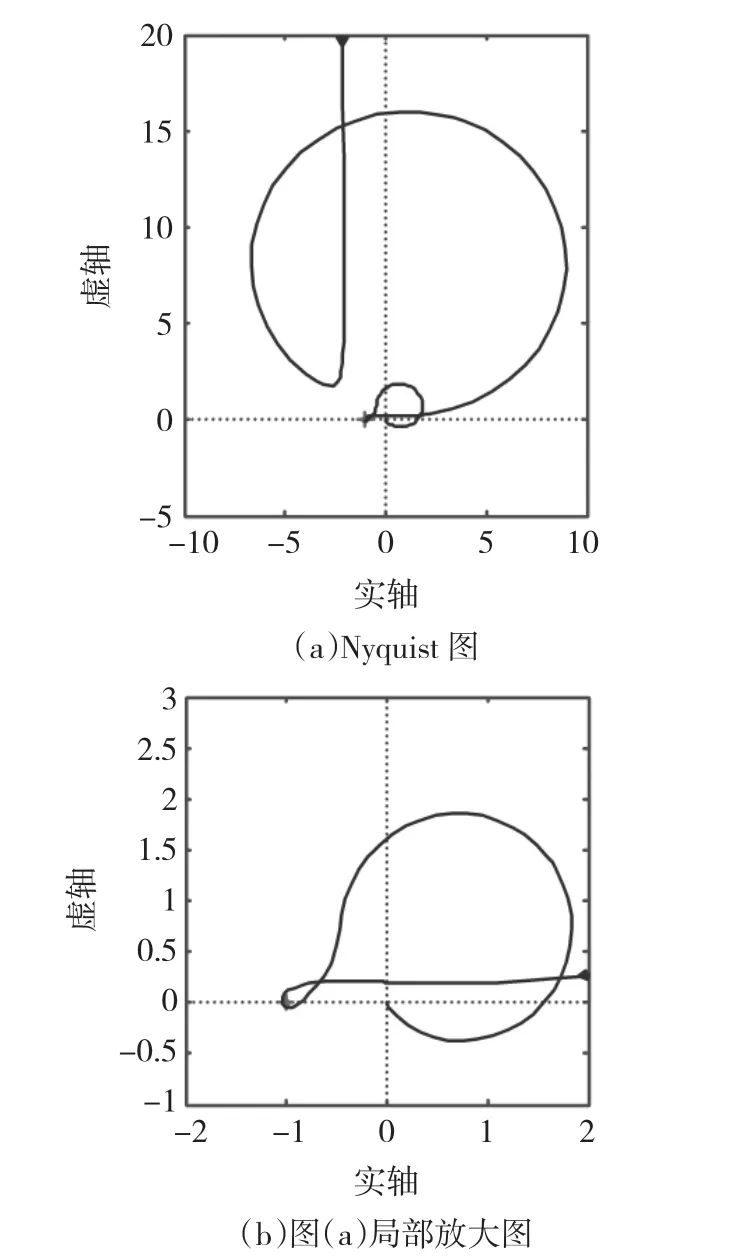
图6 位置(r)回路的Nyquist图Fig.6 Nyquist plots of the position loop(b-enlarged)

4 结语

脆弱性问题是伴随着各种优化设计理论/方法而出现的。这些优化设计虽然也包含鲁棒性，但一般都是针对对象的某种不确定性，而忽略了最基本的Nyquist判据下的鲁棒性(稳定裕度)。这样的优化设计虽然理论上是可行的，是稳定的，并可以通过仿真验证，实际上却是无法实现的。这个新的脆弱性概念对优化设计提出了一个在实际应用中可能存在的潜在问题，所以对理论和实际都是有重要意义的。

这里所说的脆弱性不同于可以用理论分析计算的控制器参数摄动，而是由于在理论分析中可能忽略稳定裕度的考虑。当然这里并不是说每个优化设计都是脆弱的，只是说优化设计存在着这种可能性。如果一个所设计的系统在实现时无法稳定工作，即无法实现这个设计，那很可能就是这个脆弱性问题。

［1］ Keel L H，Bhattacharyya S P.Robust，fragile，or optimal?［J］.IEEE Transactions on Automatic Control，1997，42(8):1098－1105.

［3］ Paattilammi J，MkilP M.Fragility and robustness:a case study on paper machine headbox control［J］.IEEE Control Systems Magazine，2000，20(1):13－22.

［4］ DOYLE J C，STEIN G.Multivariable feedback design:concepts for a classical/modern synthesis［J］.IEEE Transactions on Automatic Control，1981，26(1):4 －16.

［5］ LANZON A，PAPAGEORGIOU G.Distance measures for uncertain linear systems:a general theory［J］.IEEE Transactions on Automatic Control，2009，54(7):1532－1547.

［6］ YANG G H，WANG J L.Non-fragile H∞control for linear systems with multiplicative controller gain variations［J］.Automatica，2001，37(5):727－737.

［7］ FRANCIS B A.A Coure in H∞Control Theory［M］.Lecture Notes in Control and Information Sciences，Vol.88.New York:Springer-Verlag，1987.

［8］ DOYLE J C，FRANCIS B A，TANNENBAUM A R.Feedback Control Theory［M］.New York:Macmillan，1992.

［9］ 王广雄，何朕.控制系统设计［M］.第9章.北京:清华大学出版社，2008.

［10］ 何朕，王毅，周长浩，等.球－杆系统的非线性问题［J］.自动化学报，2007，33(5):550－553.

HE Zhen，WANG Yi，ZHOU Changhao，et al.Nonlinear problems of the bal1 and beam system［J］.ACTA Automatica Sinica，2007，33(5):550－553.

(编辑:刘素菊)

Fragility and robustness of the control system

HE Zhen， RAO Dan， WANG Guang-xiong， LIU Zhi-yuan
(School of Astronautics，Harbin Institute of Technology，Harbin 150001，China)

A novel concept of the fragility of a control system is presented，though there are some different understandings about the fragility.Fragility means that the stability margin of a system is lost during an optimal design.It is pointed out in the paper，that the fragility problem is not caused by the controller fragility，and the real cause of fragility is the design tools or criteria used in the optimal design.For example，in the H∞optimal design，the concepts of stability margin are totally absent during the design process.In MIMO system design，the singular values are used instead of the individual physical variables，so the robust stability problem of the individual loop may be ignored.This concept of fragility is different from the robustness against the parameter uncertainty of the controller.And it is helpful for understanding of the phenomenon that a well-designed system may not be stable in practice and cannot work.Therefore it is important for both theory and practice.Design examples are also presented，one of which is from the authors’own experience.

fragility;robustness;stability margin;H∞optimal design;ball-beam system

TP 273

A

1007－449X(2011)04－0080－05

2010－12－03

国家自然科学基金重点项目(61034001)

何 朕(1972—)，女，博士，教授，研究方向为控制系统设计、鲁棒控制及H∞控制等;

饶 丹(1985—)，女，硕士，研究方向为鲁棒控制;

王广雄(1933—)，男，教授，博士生导师，研究方向为控制系统设计、鲁棒控制及H∞控制等;

刘志远(1957—)，男，教授，博士生导师，研究方向为机器人控制、预测控制等。