磁悬浮开关磁阻电机建模与参数优化设计

项倩雯， 孙玉坤， 张新华

(江苏大学电气信息工程学院，江苏镇江 212013)

磁悬浮开关磁阻电机建模与参数优化设计

项倩雯， 孙玉坤， 张新华

(江苏大学电气信息工程学院，江苏镇江 212013)

针对磁悬浮开关磁阻电机参数设计问题，提出一种基于最小二乘支持向量机与粒子群优化算法的电机结构参数优化设计方法。采用三维有限元仿真建立样本空间，构建悬浮力、电磁转矩与绕组间互感的最小二乘支持向量机非参数模型;并基于该非参数模型，选择满足额定电磁转矩为约束条件，悬浮力最大且绕组间互感最小为优化目标，采用粒子群优化算法获取电机的最优结构参数。仿真结果表明:最小二乘支持向量机非参数模型精确度高，采用该优化设计方法设计的磁悬浮开关磁阻电机具有悬浮承载力强、耦合小、易于控制的优点，并且该优化设计方法算法简单、操作方便。

磁悬浮开关磁阻电机;最小二乘支持向量机;粒子群算法;非参数建模;优化设计

0 引言

开关磁阻电机具有超高速、低功耗运行的特点，但是高速、超高速电机的突出问题是机械磨损问题。机械摩擦不仅增加了转子的摩擦阻力，降低轴承寿命，还产生振动与噪声，且会使部件发热，润滑性能变差，绕组发热，温升增大，从而导致电机性能变差，降低运行效率。针对这些问题，有学者将磁悬浮轴承与开关磁阻电机技术有机结合，提出了磁悬浮开关磁阻电机(BSRM)的概念，解决了开关磁阻电机轴承磨损、振动、噪声、临界转速和输出功率难以提高等难题，可实现超高速、大功率运行［1－3］。

文献［2］分析了BSRM的运行机理与控制策略，文献［3］研究了磁饱和情况的模型建立与控制方法。针对给定功率的BSRM结构与电磁参数设计问题，文献［4］基于BSRM的数学模型，在分析电机性能的基础上设计了电机参数，但由于忽略磁饱和影响，设计精确度较差。文献［5］基于二维有限元模型，给出了BSRM电机参数的优化设计方法，但由于二维有限元计算无法处理端部磁场效应，精确度差。

本文以一台三相12/8极BSRM为对象，基于三维有限元方法(FEM)计算不同结构参数下的电磁输出，建立样本数据库，并构建BSRM的最小二乘支持向量机(LS－SVM)非参数模型;在满足额定电磁转矩的条件下，以悬浮力最大、绕组间互感最小为目标，利用粒子群(PSO)优化算法获取电机最优结构参数。

1 有限元仿真分析

磁悬浮开关磁阻电机的三维有限元模型如图1所示。以A相为例，径向相对的四极绕组串联而成的是旋转力绕组Nma，径向相对的两极绕组串联而成的分别为悬浮力绕组Nsax与Nsay。若A相旋转力绕组与悬浮力绕组同时施加电流，每个径向自由度上必会出现一端磁场增强，另一端磁场减弱，从而产生径向上的悬浮力，如图2所示。由于电机运行时悬浮力必须支承转轴且为径向扰动提供恢复力，因此其承载水平是磁悬浮电机稳定悬浮的关键。而BSRM的复杂结构使其旋转力绕组与悬浮力绕组间磁路共有、互感大、耦合强，难以实现两者电流的独立控制与电机的高速稳定运行［6］。

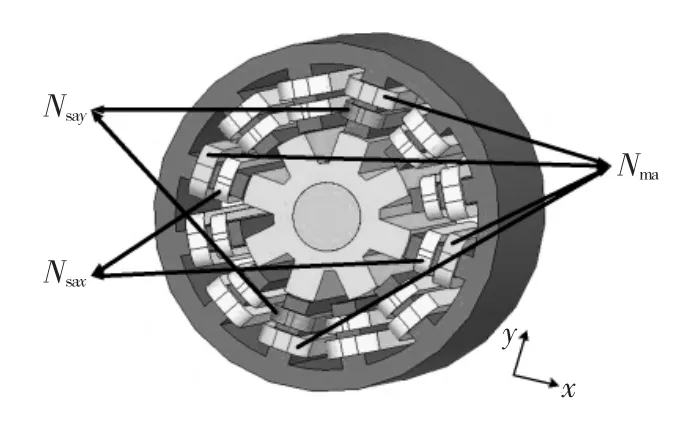
图1 BSRM三维有限元模型Fig.1 3D FEM model of the BSRM

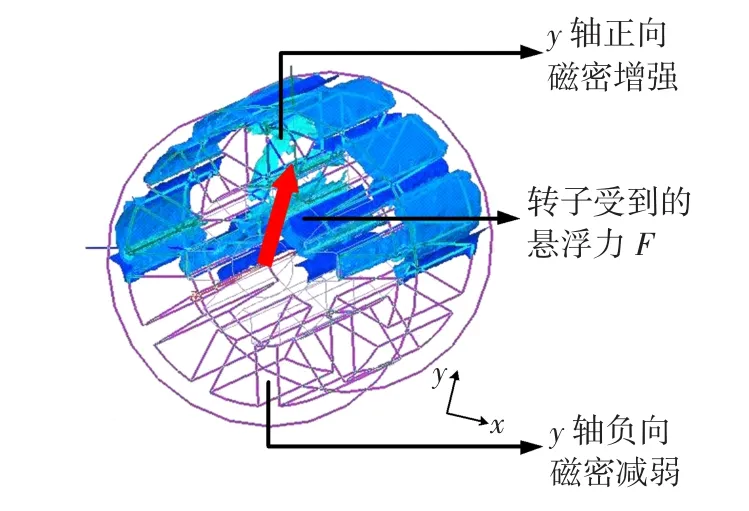
图2 悬浮力产生机理Fig.2 Principle of radial force production

通过对BSRM通电相等效磁路图的计算可知，各电磁输出受通电相定子每个齿极下气隙磁导的影响最大［7－8］。从通电相定子极下气隙磁通路径(图3所示)可以看出，电机定、转子极结构参数变化会改变磁通路径，继而改变气隙磁导，影响悬浮力、转矩与绕组间互感。

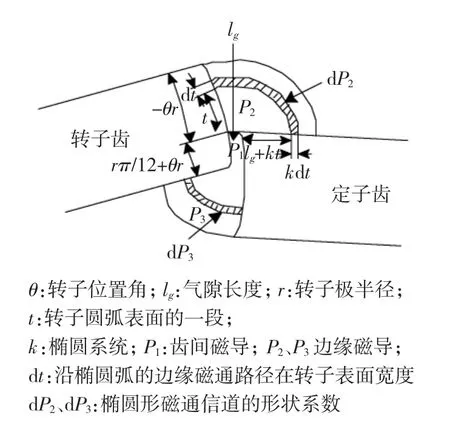
图3 气隙处磁路分割示意图Fig.3 Magnetic paths partition of air gap

BSRM参数优化的目的是通过合理设计电机的结构参数，使电机转矩满足额定电磁转矩的条件下，径向悬浮力最大，且旋转力绕组与悬浮力绕组间互感最小。

2 LS-SVM非参数模型

2.1 样本空间获取

为了尽可能多地获得电机参数变量空间中具有代表性的样本空间，采用正交试验设计方法与随机组合方法相结合的混合试验设计方法，不但能获得具有很强代表性的样本数据点，而且样本总量上也满足了电机回归建模的需要。正交试验设计利用设计变量各水平之间的互相均匀搭配、设计方案产生的数据点在设计变量空间的均匀分布，从而获得能够较全面地代表和反映设计变量对研究系统性能特征的影响规律的数据;随机组合方法是在各个因素取值的上下限范围内采用等距抽样法抽取一批试验取样点，使其满足模型回归时所需的样本总量要求［9］。BSRM考察因素和取值空间点如表1所示。

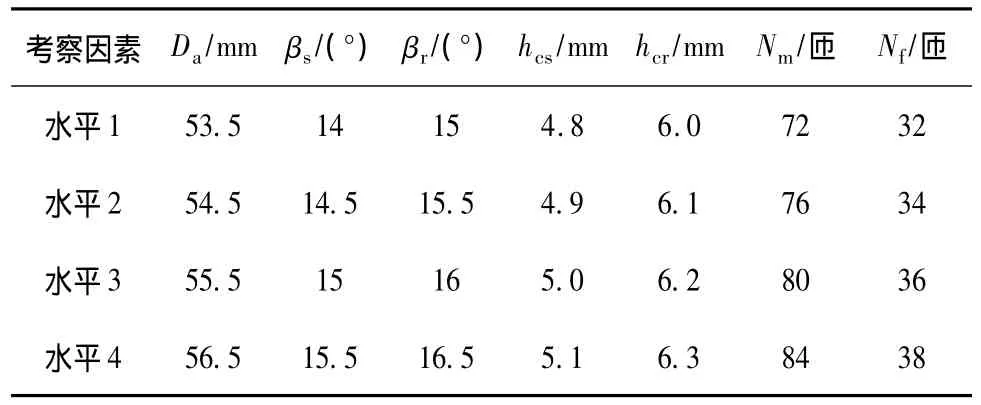
表1 BSRM结构参数因素水平表Table 1 Level of the structural parameters of BSRM

样本空间样本数为47，从中随机抽取800组数据作为训练样本，用于模型回归，其中包括64组正交空间的数据。

2.2 LS-SVM非参数建模

三维有限元方法计算速度慢，不适合参数优化过程中的在线计算，为此，建立BSRM结构参数与悬浮力、互感与转矩的快速计算模型为

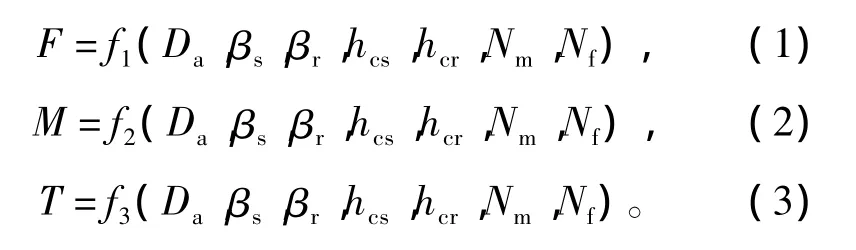
其中:F为悬浮力;M为旋转力绕组与悬浮力绕组间互感;T为转矩;Da为转子外径;βs为定子极弧;βr为转子极弧;hcs为定子轭高;hcr为转子轭高;Nm为旋转力绕组匝数;Nf为悬浮力绕组匝数。

式(1)～式(3)的数学解析式难以获得，只能用非参数估计的方法逼近。通过FEM测得不同结构参数下的电机悬浮力、互感与转矩，构建样本数据空间，利用 LS-SVM建立 F、M与 T的快速计算模型［10－11］。

为了验证LS-SVM建立的非参数模型的可靠性，随机抽取100组不同于训练样本的测试样本。并在测试样本中选取一组样本，其LS-SVM模型与FEM模型的输出比较如图4所示。

定义评价模型估计效果的性能指标如下:

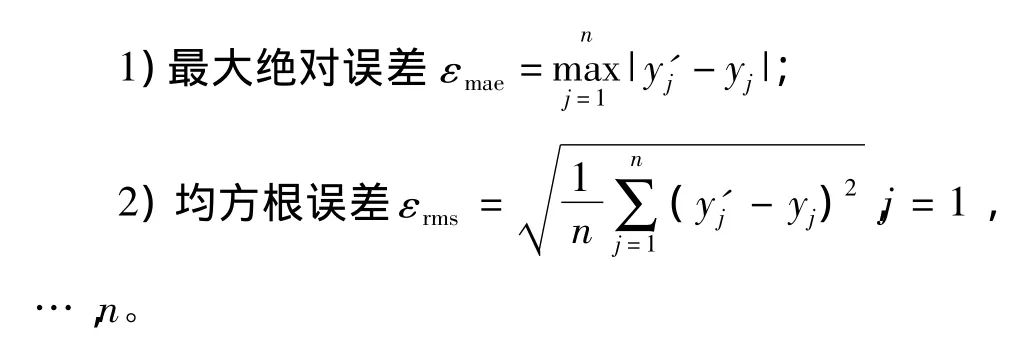
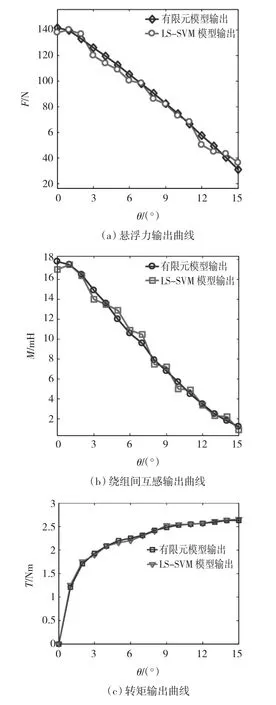
图4LS-SVM模型与FEM模型输出比较Fig.4 The compare results between models of LS-SVM and FEM

通过计算可知F、M与T的LS-SVM模型估计能力为

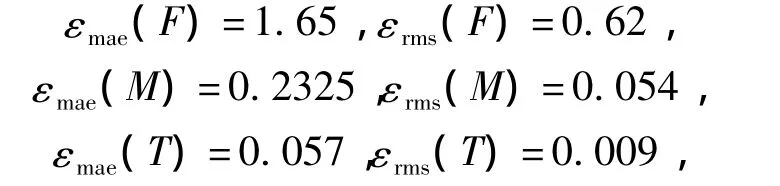
表明该模型预测效果好［12－13］。

为了验证LS-SVM建立的非参数模型的计算速度，相同样本的LS-SVM模型与FEM模型计算速度比较如表2所示。

表2 LS-SVM模型与FEM模型计算速度比较Table 2 Results of calculating speed between the LS-SVM and FEM

综上，基于LS-SVM非参数模型预测精度高，速度快，因此非常适合参数优化过程中的在线计算。

3 BSRM粒子群参数优化方法

BSRM参数优化的目标是:1)悬浮力最大;2)互感最小。其约束条件为:转矩不小于额定电磁转矩。为此优化问题可转化为

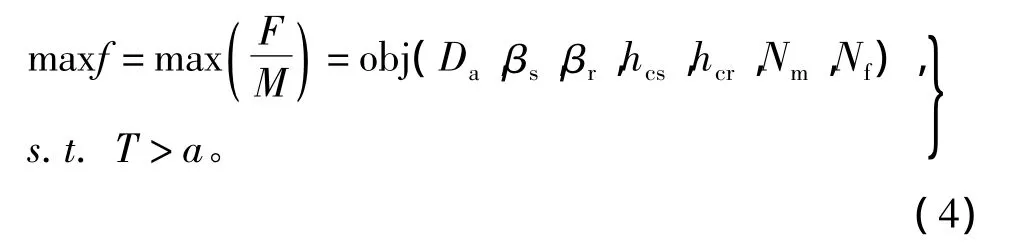
式中，a为实际约束值。

优化模型(4)是一个非线性、多极值、多参数的大规模计算问题，不满足可微、连续等严格的数学条件，难以采用常规优化算法。因此本文采用粒子群优化算法对电机的参数进行优化。

3.1 粒子群优化算法

粒子群优化算法是一种基于群体智能方法的演化计算理论，具有较高的搜索效率。设复杂空间的维数为m，PSO的搜索过程通过循环迭代来完成，每次循环，粒子i通过动态的跟踪自身最优值pbest={pi1，pi2，…，pim}及群体最优值 gbest={g1，g2，…，gm}完成其速度和位置的更新［14］。设 vi={vi1，vi2，…，vim}与 xi={xi1，xi2，…，xim}分别为粒子 i的速度和位置。粒子的转移速度和位置按

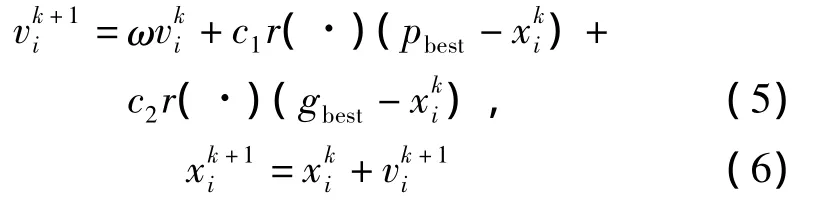
更新。其中:k为迭代次数;ω为惯性权重系数;r(·)为(0，1)之间的随机数;c1，c2为学习因子，－Vmax≤≤Vmax，Vmax是事先确定的正常数，限制速度的变化范围。迭代终止条件一般选为最大迭代次数或粒子群迄今为止搜索到的最优位置满足预定最小适应阈值。

3.2 粒子群优化BSRM参数

粒子群优化BSRM结构参数的计算流程如图5所示。通过试算，确定PSO的参数如下:粒子个数为50，粒子维数为7维，循环次数为1 000，惯性权重ω由0.95随循环次数线性递减至0.45，学习因子c1=c2=2.05，优化空间如表3所示。定义适应度函数［15］

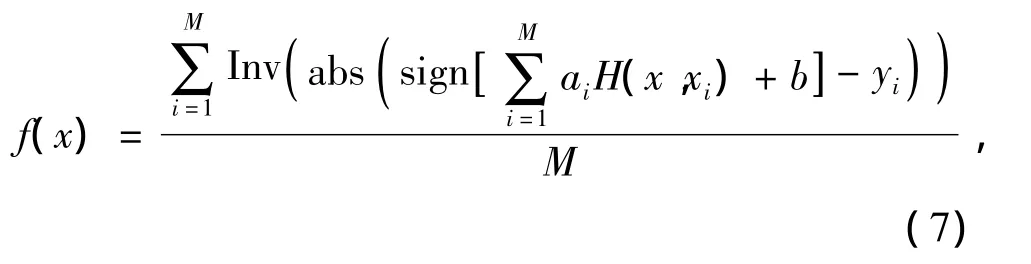
其中，yi为实测值。

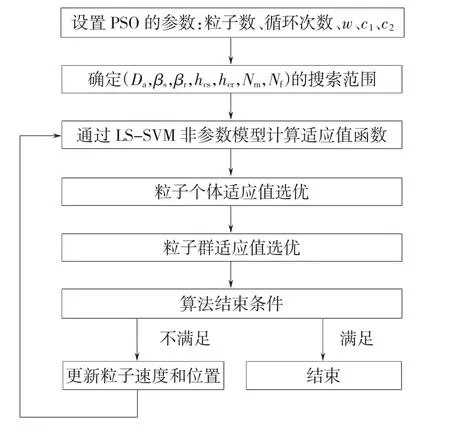
图5 BSRM参数优化流程Fig.5 The flow chart of parameter optimization

采用粒子群算法进行搜索得到一组优化结果，如表4所示。

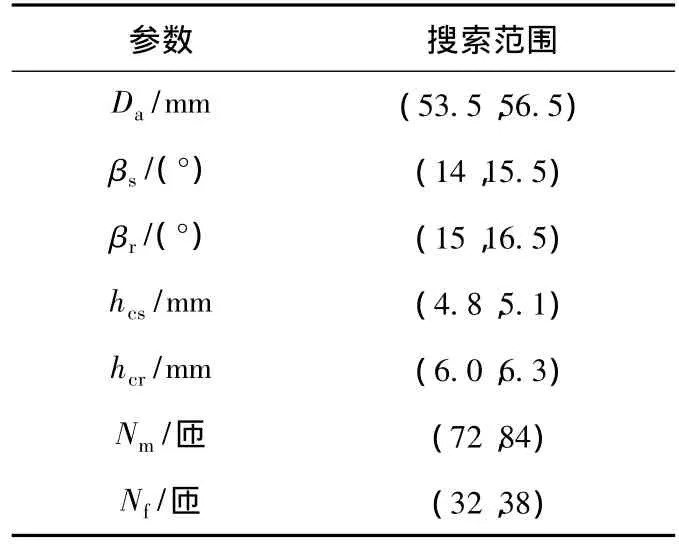
表3 粒子的搜索空间Table 3 The search space of every particle

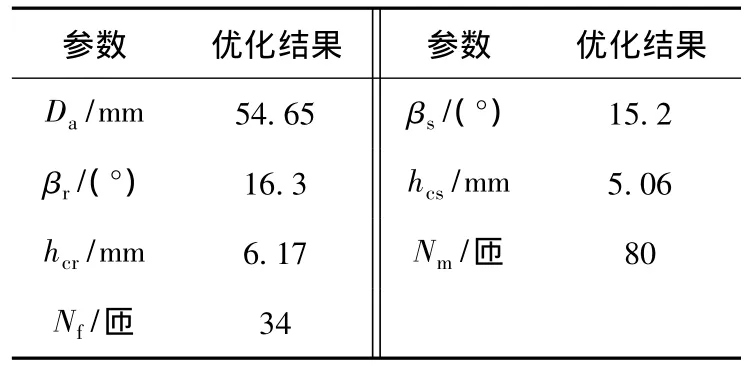
表4 PSO优化结果Table 4 Optimization results of PSO

3.3 优化结果分析

设表1中水平1、水平4分别对应电机1、电机4。当通以额定悬浮力绕组电流与额定旋转力绕组电流时，优化电机与电机1、电机4的性能比较如图6所示，图中可看出:

1)电机1、优化电机、电机4的平均转矩分别为2.15 N·m、2.21 N·m、2.37 N·m。

2)电机1、优化电机、电机4的平均悬浮力分别为73.15 N、97.07 N、100.13 N。

3)电机1、优化电机、电机4的平均绕组间互感分别为8.77 mH、9.21 mH、11.59 mH。

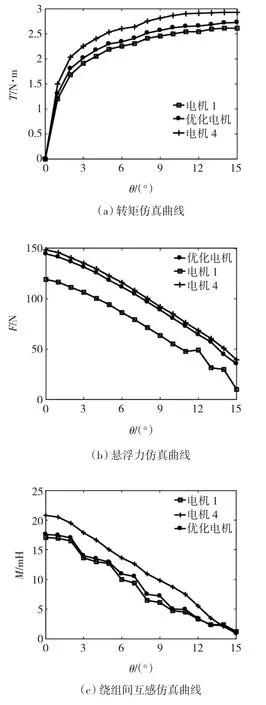
图6 优化结果的仿真分析Fig.6 The simulating analysis of optimization results

3台电机的转矩均达到设计值2.15 N·m。电机1的互感虽小，但径向悬浮力亦小，表明径向悬浮承载能力弱，径向抗扰动性能差。电机4的悬浮力虽大，但互感亦大，表明电机磁场饱和，悬浮力绕组与旋转力绕组间的耦合增强，加大电机控制难度。综合比较悬浮力与互感，优化电机的性能优于电机1与电机4，说明粒子群优化获得的结果是可靠实用的。

4 结语

针对磁悬浮开关磁阻电机非线性、强耦合的特点，利用LS－SVM建立磁悬浮开关磁阻电机非参数模型，结合粒子群算法优化结构参数，得到最优解，使相同条件下电机既能产生足够转矩，又满足径向承载能力强、耦合小、电流控制易于实现的要求。仿真结果证明了优化结果的可靠性，为BSRM优化设计探索出一种有效的方法。

［1］ 詹琼华.开关磁阻电动机［M］.武汉:华中理工大学出版社，1992.

［2］ TAKEMOTO M，SUZUKI H，CHIBA A，et al.Improved analysis of a bearingless switched reluctance motor［J］.IEEE Transactions on Industry Applications，2001，37(1):26 －34.

［3］ TAKEMOTO M，CHIBA A，AKAGI H，et al.Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation［J］.IEEE Transactions on Industry Applications，2004，40(1):104 －112.

［4］ 范冬，杨艳，邓智泉，等.无轴承高速开关磁阻电机设计中的关键问题［J］.电机与控制学报，2006，10(6):547－552.

FAN Dong，YANG Yan，DENG Zhiquan，et al.The key technology on designing a high-speed bearingless switched reluctance motor［J］.Electric Machines and Control，2006，10(6):547－552.

［5］ LIU Z，DENG Z，CAI J，et al.Optimal design of a bearingless switched reluctance motor［C］//Proceeding of 2009 IEEE International Conference on Applied Superconductivity and Electronmagnetic Devices.Chengdu，China:IEEE，2009:241 －245.

［6］ 孙玉坤，任元，黄永红.磁悬浮开关磁阻电机悬浮力与旋转力的神经网络逆解耦控制［J］.中国电机工程学报，2008，28(9):81－85.

SUN Yukun，REN Yuan，HUANG Yonghong.Decoupling control between radial force and torque of bearingless switched reluctance motors based on neural network inverse system method［J］.Proceedings of the CSEE，2008，28(9):81－85.

［7］ 孙玉坤，吴建兵，项倩雯.基于有限元法的磁悬浮开关磁阻电机数学模型［J］.中国电机工程学报，2007，27(12):33－40.

SUN Yukun，WU Jianbing，XIANG Qianwen.The mathematic model of bearingless switched reluctance motor based on the finite-element analysis［J］.Proceedings of the CSEE，2007，27(12):33－40.

［8］ 孙玉坤，刘羡飞，王德明，等.基于有限元分析的磁悬浮开关磁阻电机数学模型的全角度拓展［J］.电工技术学报，2007，22(9):34－39.

SUN Yukun，LIU Xianfei，WANG Deming，et al.Extension of mathematical model to full angle for bearingless switched reluctance motors based on finite － element analysis［J］.Transactions of China Electrotechnical Society，2007，22(9):34－39.

［9］ 赵选民.试验设计方法［M］.北京:科学出版社，2009.

［10］ NELLO Cristianini，JOHN Shawe－Taylor.支持向量机导论［M］.北京:电子工业出版社，2004.

［11］ 方瑞明.支持向量机理论及其应用分析［M］.北京:中国电力出版社，2007.

［12］ 司利云，林辉，刘震.基于最小二乘支持向量机的开关磁阻电动机建模［J］.中国电机工程学报，2007，27(6):26－30.

SI Linyun，LIN Hui，LIU Zhen.Modeling of switched reluctance motors based on LS-SVM［J］.Proceedings of the CSEE，2007，27(6):26－30.

［13］ 尚万峰，赵升吨，申亚京.遗传优化的最小二乘支持向量机在开关磁阻电机建模中的应用［J］.中国电机工程学报，2009，29(12):65－69.

SHANG Wanfeng，ZHAO Shengdun，SHEN Yajing.Application of LSSVM optimized by genetic algorithm to modeling of switched reluctance motor［J］.Proceedings of the CSEE，2009，29(12):65－69.

［14］ 纪震，廖惠连，吴青华.粒子群算法及应用［M］.北京:科学出版社，2009.

［15］ 郭亮，卢琴芬，叶云岳.基于粒子群算法的直线振动发电机优化设计［J］.电机与控制学报，2008，12(4):442－446.

GUO Liang，LU Qinfen，YE Yunyue.Optimization design of linear reciprocating generator based on particle swarm algorithm［J］.Electric Machines and Control，2008，12(4):442 －446.

(编辑:于智龙)

Modeling and parameters optimal design of bearingless switched reluctance motor

XIANG Qian-wen， SUN Yu-kun， ZHANG Xin-hua
(Electronic and Information Engineering College，Jiangsu University，Zhenjiang 212013，China)

For the parameters design of bearingless switched reluctance motor(BSRM)，a structure parameters’optimal design method was proposed based on the least squares support vector machine(LSSVM)and the particle swarm optimization(PSO).It obtained sample space by 3D finite element simulation and then built LSSVM nonparametric models of radial levitation force，torque and mutual inductance.Based on these models，it chose rated torque reached as constraint condition，and selected maximal radial levitation force，minimal mutual inductance as optimal objective.And then，the optimal parameters of BSRM were obtained by PSO searching.The simulation results prove that the LSSVM nonparametric models have high accuracy and the optimized motor has strong suspension bearing capacity，weak coupling，and simple control by simple and handy arithmetic.

bearingless switched reluctance motors;least squares support vector machine;particle swarm optimization;nonparametric modeling;optimal design

TM 352;TM 153

A

1007－449X(2011)04－0074－06

2010－09－12

国家自然科学基金(61074019，60774044)

项倩雯(1982—)，女，博士研究生，讲师，研究方向为磁悬浮开关磁阻电机设计;

孙玉坤(1958—)，男，博士，教授，博士生导师，研究方向为磁悬浮电机的控制与应用;

张新华(1973—)，男，博士研究生，讲师，研究方向为电机调速。