一种新型自补偿组合式机械密封的设计与应力分析

2011-02-09颜伟，胡勇

制造业自动化 2011年4期

颜伟，胡勇

（1.四川交通职业技术学院自动化工程系，成都 611130；2、四川理工学院机电系，自贡 643000）

0 引言

目前，国内电石反应器转轴与缸筒之间，多采用石墨盘根或聚四氟乙烯( PTFE)V形圈填料函密封。通过调查国内某企业运行的32台电石反应器（传动轴径Φ270mm，工作压力10～20kPa，工作温度85～110℃。）密封装置，发现这种密封装置的平均使用寿命仅约483小时，给设备的正常运转带来不良影响。

解剖失效的密封件发现：重叠的V形圈间歇被电石渣颗粒充填，V形圈内外侧面严重磨损。分析其原因是：乙炔气体中的磨粒在压力作用下进入密封面间隙，加剧了密封面的磨损、使密封面间隙加大；密封面间隙加大又使更多的磨粒进入密封面，最终导致密封的失效。

根据上述分析，要提高密封的密封效果和使用寿命，关键是要阻止磨粒进入密封腔和自动补偿密封面的磨损。为此，本研究设计了一种新型自补偿组合式机械密封（见图1）：前级密封由二级油沟、迷宫或它们的组合构成，主要功用是阻止或减少乙炔气体中的磨粒（电石渣颗粒）渗入后级密封；后级密封由一级锥形端面密封（弹簧、聚四氟乙烯锥形静环、锥形轴套动环、O形橡胶圈等）构成，主要功用是密封乙炔气体外泄。锥形端面密封在弹簧和乙炔气体压力作用下，具有自动补偿密封面磨损、保障密封的功能，是本设计的关键环节。

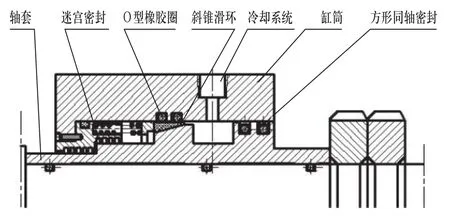
图1 自补偿组合式机械密封装置

锥形端面密封元件的应力分析与密封性能等的研究报道尚不多见。本研究利用ANSYS软件，对7组不同厚度的锥形静环进行有限元分析并仿真求解，旨在研究和分析：

1)在安装状态下锥形静环需要的弹簧推力；

2)在安装和工作状态下，密封面及其他接触面的接触压力和O形圈的Von.mises应力；

3)不同厚度锥形静环的密封效果。

通过上述问题的有限元分析并仿真求解，为本文设计的新型自补偿组合式机械密封的进一步研究、结构设计及使用，提供理论依据。

1 应力分析几何模型

本研究设计的自补偿组合式机械密封的应力分析几何模型如图2所示。

图2 自补偿组合式机械密封几何模型

其中：

b－轴套沟槽宽度；b1－轴套两沟槽临边距离；

d0－O形圈直径； δ－初始状态时缸筒下边缘与锥形静环上边缘的距离；

h－锥形静环左侧厚度；

θ －锥形静环斜边与水平线的夹角；

压缩弹簧（小弹簧结构形式）作用在锥形静环的左端面；压缩弹簧推动锥形静环右移、使其紧紧地贴合在转轴轴套（动环）斜锥面上，形成机械密封面；锥形静环还迫使O形密封圈产生一定的预压缩量，使密封面具有一定的预接触压力。图2所示模型，也是自补偿组合式机械密封的安装状态。

工作状态时，密封缸内乙炔气体的压力和弹簧推力，共同作用于锥形静环左侧面上，推动锥形静环微量右移； O形密封圈压缩量增大，使密封面的接触压力增大，克服密封面的液膜压力使两接触面始终紧紧贴住，达到良好的密封效果。

当锥形静环厚度因磨损减小后，O形密封圈压缩量随之减小，则作用在锥形静环上的力平衡关系被打破；弹簧推力和乙炔气体的压力将推动锥形静环进一步微量右移，增大O形密封圈压缩量，到达一个新的平衡位置，从而起到自动跟随、补偿锥形密封面磨损的作用。

由此可见，锥形静环厚度变化及其相关应力、O形圈压缩量变化及其相关应力直接影响密封效果和密封装置寿命，是本研究设计与应力分析的重点所在。

2 有限元模型

1)基础数据：

O形密封圈和沟槽的设计均按照国标 (GB 3452.1-92) 设计，采用腈基丁二烯橡胶 (NBR)，硬度为85IRHD，弹性模量E = 14.04MPa，泊松比υ= 0.499，摩擦系数为0.2。锥形静环采用聚四氟乙烯，硬度（邵氏）为55 IRHD, 压缩弹性模量E =280MPa，泊松比υ= 0.40,摩擦系数为0.04。边界密封缸筒和轴套弹性模量E = 2×10E5 MPa，泊松比 υ= 0.3。

2)有限元模型：

根据密封结构的几何形状、材料、边界条件的特点和 ANSYS功能，采用平面轴对称有限元计算模型。建立的锥形端面密封件变形前有限元模型如图3所示。

对其进行有限元分析时，由于边界条件及载荷的复杂性，故将密封圈及密封结构的轴、滑环作为整体进行分析，其中所涉及的几何非线性、橡胶体超弹材料非线性、边界 (状态 )非线性知识和进行的一些相关假设,限于篇幅这里就不再累赘，可见有关文献。

图3 有限元模型

该有限元模型中,橡胶单元采用超弹性单元plane183，斜锥滑环、边界轴和轴套单元采用单元PLANE82 ，接触单元由接触单元CONTAI172和目标单元TARGE169配对组成。在O形密封圈与缸筒、O形密封圈与锥形静环、锥形静环与轴套（动环）之间共建立了9个接触对，利用它们模拟轴套与锥形静环、锥形静环与橡胶弹性体、橡胶弹性体和缸筒之间的接触。共划分出4154个单元，11832个节点。

3)边界及荷载：

假设缸筒及轴套静止，锥形静环可在O形圈与轴套之间往复运动。安装状态时，O形密封圈压缩量取0.2mm，压缩率为2.86%（O形密封圈直径为7mm）。计算所需弹簧推力时，以位移荷载加载在锥形静环左侧，从结果中计算出的该处支反力，即为所需弹簧推力值。工作状态的仿真，是到达安装状态后，在锥形静环左侧面及左侧O形密封圈上下两接触点左侧、施加0.2MPa的工作内压而进行的计算。

3 应力分析

3.1 锥形静环需要的弹簧推力

弹簧推力除保证主机在起动、停车或介质压力波动时，使密封面能紧密接合外，还要克服相关元件与锥形静环表面间的摩阻力，使锥形静环能追随锥形端面的磨损沿轴向移动。弹簧推力同时还要克服O形密封圈和锥形静环抵抗自身变形产生的抗力。随锥形静环厚度的增加，其自身抵抗变形能力增强，需要更大的弹簧推力。

仿真实验结果：

1)安装状态下，锥形静环厚度增加、锥形静环需要的弹簧力呈上升趋势：厚度h=8mm时，轴向弹簧推力720N；厚度h=20mm时，轴向弹簧推力增大到870N。

2)达到安装状态后，O形密封圈实现预压缩量，产生的Von.mises应力随厚度h的增加，呈下降趋势：h=8mm时，最大应力值为0.722MPa，h=20mm时，最大应力值为0.688MPa。其变化量仅为0.034MPa，所以，可以近似认为O形密封圈变形相同。

3.2 接触压力的分布情况

锥形密封面及其他接触面的Von.mises应力：安装和工作状态下，密封结构的Von.mises应力分布情况如图4、5所示，安装和工作状态下最大应力值都出现在其他接触面处, 密封面处的应力值小于其他接触面的值。由此，可认为密封的效果主要取决于锥形静环与轴套（动环）之间形成的密封面及密封面的接触应力。

O形圈的Von.mises应力：

经ANSYS软件分析，工作状态时，O形密封圈的Von.mises应力值和压缩率变化随锥形静环厚度h的增加基本呈线性增长，但是，数值都较小。当h=20mm时，最大Von.mises应力值为2.01MPa，压缩率为10.53%。说明在此工作条件下，O形密封圈的工作状态良好。

图4 h=8mm时安装状态下Von.mises应力分布

图5 h=8mm时工作状态下Von.mises应力分布

图6 密封面上最大接触压力与锥形静环厚度的关系曲线

3.3 锥形静环厚度对接触应力的影响

保证密封的必要条件是密封界面上的最大接触压力大于或等于工作介质压力。图6、7为不同壁厚锥形静环在安装和工作状态下最大接触压力与滑环厚度关系曲线。

由图6可知，密封面最大接触压力随锥形静环厚度h的增大先下降再上升。分析原因，当锥形静环厚度较小（h=8～14mm）时，随锥形静环厚度增加，接触面受锥形静环局部变形影响逐渐减小，导致最大接触压力呈下降趋势变化；当锥形静环厚度较大（h=14～20mm）时，接触面不受锥形静环局部变形影响，随锥形静环厚度增加，滑环左侧面积增大，则受到更大由工作内压提供的轴向推力，造成最大接触压力随锥形静环厚度增加呈上升趋势变化。

虽然密封面处最大接触压力随锥形静环厚度而变化，但其接触压力总是大于工作介质压力, 说明此密封结构随锥形静环的磨损，仍可保证密封的要求，具有“跟随补偿”作用。

由图7可知，其他接触面的接触压力随锥形静环厚度增加而变大，并且远大于工作压力。综上分析，在锥形静环设计提供的磨损裕量条件下，在整个使用周期内都能实现良好密封，具有良好的密封功能。