连续埋地管线沉陷情况下可靠度分析
2011-02-08柳春光冯晓波
柳春光, 冯晓波
(1.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024;2.中建国际设计顾问有限公司,上海200235)
0 引 言
随着国民经济的日益发展以及城市现代化速度的加快和规模的壮大,生命线工程在人们日常生活中的作用也越来越重要.埋地管线是生命线工程的一个重要组成部分,主要运用于输水、输气、输油、通信、供电、排水等与人们生活有着直接关联的领域,其一旦遭到破坏,将给人们的生活和城市的工业生产带来严重的影响,因此,自1971年美国的圣尔南多大地震对埋地管线造成严重的影响后,埋地管线的安全问题就一直受到人们的关注.我国地域广阔,资源丰富,但是分配不均,比如西气东输、南水北调等重大工程都需要埋地管线的连接,这些埋地管线将穿越断层区、沉陷区、液化区,因此,对于跨越这些区域的埋地管线进行安全可靠性分析十分重要,进行安全可靠性分析后对埋地管线进行抗震设计,这样地震发生时,穿越这些区域的埋地管线才不至于遭到破坏.因此分析埋地管线在地面大位移作用下的可靠度是十分必要的,本文主要运用均值一次二阶矩法和蒙特卡罗法分析埋地管线在地面沉陷位移、材料性能参数、内水压力等随机参数下的可靠度,希望能为沉陷区埋地管线的抗震设计提供一定理论基础.
1 埋地管线可靠度计算方法
1.1 均值一次二阶矩法
设X1,X2,…,X n表示包括与抗力和荷载有关的随机变量,由这些随机变量表示的功能函数为[1]
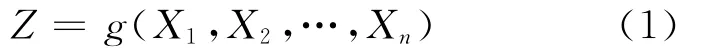
显然,此时的功能函数Z有3种状态:Z=0,极限状态;Z≥0,安全状态;Z≤0,失效状态.
将结构功能函数在Xi(i=1,2,…,n)展开为泰勒级数并保留至一次项,得到
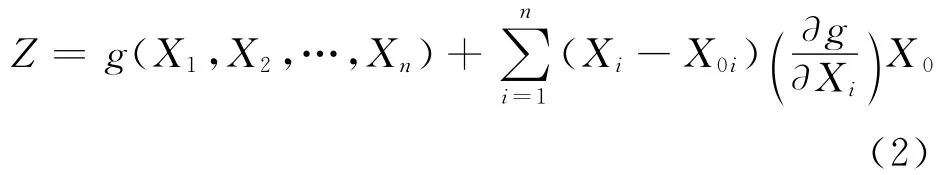
对上式分别取均值和方差得

引入量纲一参数——可靠度指标

则失效概率

从式(6)可以看出,β与Pf有着一一对应的关系.
1.2 蒙特卡罗法
蒙特卡罗法[1]又称随机抽样法,是一种通过随机变量的统计试验或者随机模拟来求解问题的数值方法.在当前结构可靠度的计算方法中,蒙特卡罗法被认为是一种非常精确的计算方法.在大型有限元软件ANSYS中,蒙特卡罗法的抽样方法可以分为直接法、拉丁超立方法、自定义方法3种.
2 连续埋地管线可靠度的算例分析
2.1 算例资料[2]
钢管材料为X-65型钢,管线直径为300 mm,管线壁厚为7 mm,泊松比为0.3,管线埋深为1.5 m,弹性模量E=210 GPa;假设管线埋设于亚黏土中,土的容重为18 k N/m3,土体的摩擦角为30°,取土弹簧的屈服位移u0=0.007 5 m.计算时暂不考虑外界振动、温度的变化以及初始装配应力等因素的影响.
假设本文所采用的管线是由刚性管线连接而成的直管,国内外众多实验结果表明:抗震设计中管线的性能指标一般是由管线的最大轴向应力应变控制.对于大应力大应变的问题,工程上常用的是三折线管材模型,一般将管材的形变特征分为3个状态:弹性、弹塑性、塑性.本文所采用管材的本构关系如图1所示,管材特性为E1=2.1×105MPa,E2=1 808 MPa,σ1=496.8 MPa,σ2=564 MPa,材料的屈服应变ε1=0.002 4,材料容许拉伸应变ε2=0.04,材料拉伸极限应力对应的应变εm=0.145,材料拉断时所对应的应力σb=508 MPa.

图3 3个方向土弹簧的非线性模型Fig.3 Nonlinear model of the soil spring in three directions
本文将管线离散成四节点薄壳单元,沿管线周围分成8个单元,沿管轴向薄壳单元的长度为0.1 m,采用等效弹簧边界来代替远处无限长管线的变形,采用三向土弹簧来模拟管土之间的相互作用,假设场地两侧的土质情况相同,取一侧场地的土质条件进行分析,这样可以提高有限元分析效率.根据上述的条件,通过计算后得到等效弹簧的力F与位移u的关系曲线如图2所示.3个方向土弹簧的模型如图3所示.
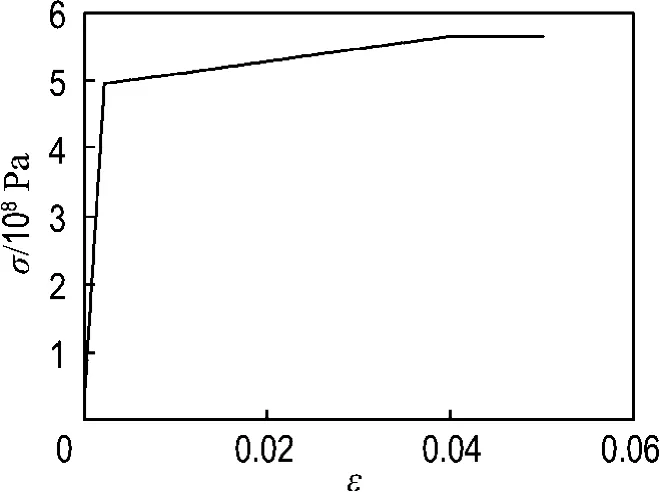
图1 X-65钢管本构关系Fig.1 The constitutive relation of X-65 steel pipe
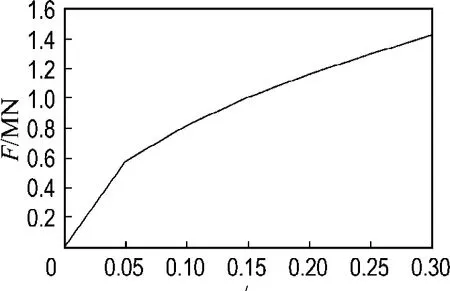
图2 等效弹簧外力与位移曲线Fig.2 The force-displacement curve of equivalent spring
2.2 应用均值一次二阶矩法计算连续埋地管线的可靠度
2.2.1 不考虑管道内水压力时埋地管线的可靠度 采用壳有限单元分析埋地管线在沉陷大位移作用下的可靠度,则埋地管线在沉陷情况下管内最大轴向拉伸应变的简化公式[3]为
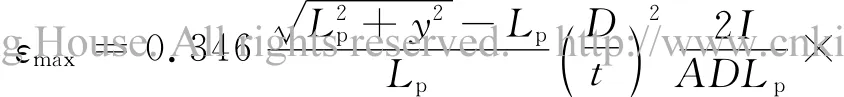


进一步得到埋地管线在沉陷位移、管径、管壁等随机变量下的功能函数:
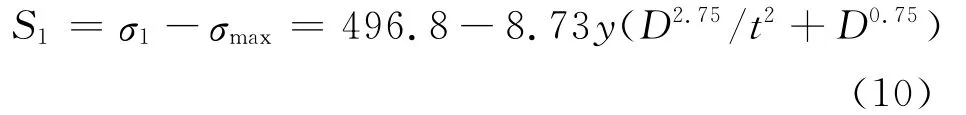
假设各个随机变量服从正态分布,已知各个随机变量的均值与方差,通过Matlab编程计算得到结构的可靠度指标β=0.190 7,通过查表可得失效概率Pf=42.45%,从而得到结构的可靠概率P为57.55%.
2.2.2 考虑管道内水压力时埋地管线的可靠度作者通过借鉴前人的计算公式推出了不考虑管道内水压力时埋地管线可靠度的简化公式,接下来主要分析研究考虑管道内水压力时埋地管线可靠度计算的简化公式,对于直管道,内水压力p产生的管道环向应力σθ和纵向应力σl分别为[4]

式中:μ为泊松比.
相应管线内最大的轴向应力为

由式(11)和(12)可以得到管线的最大组合应力为
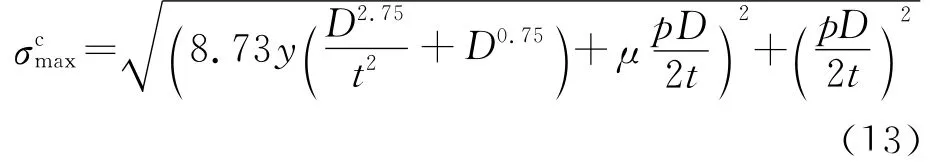
由此可得埋地管线在沉陷位移、管径、管壁以及管道内水压力等随机变量下的功能函数为
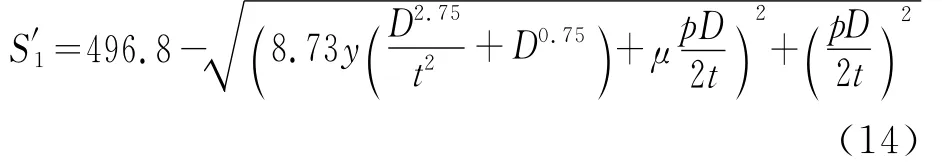
采用类似的方法计算,得到结构的可靠度指标β=-0.952 2,通过查表得到结构的失效概率Pf=83.03%,从而得到结构的可靠概率为16.97%.
2.3 应用蒙特卡罗法计算连续埋地管线的可靠度
2.3.1 输入输出变量参数的定义 在确定分析文件正确前提下,直接进入ANSYS中的可靠性设计模块(PDS),进行构件的可靠性分析.在进行结构的可靠性分析前,要对输入输出变量进行参数化定义.本节计算所涉及的参数[5~12]如下:假定所有参数都服从正态分布,沉陷位移均值珔y=0.3 m,变异系数δy=0.1;压强均值珚p=8 MPa,δp=0.1;管道直径均值珡D=0.3 m,δD=0.01;管道壁厚均值珋t=0.007 m,δt=0.05.
2.3.2 功能函数的建立 对于连续埋地管道而言,判断管线是否失效的依据是管道所受的组合应力是否超出管道材料的屈服应力和极限应力.埋地管线遭受沉陷大位移作用时,沉陷位移和管道内水压力共同作用使管壁内产生压应力和拉应力.
当σmax>σ1时,管线处于正常使用极限状态;当σmax>σ2时,管线处于承载力极限状态.对于沉陷区埋地管线主要考虑的是其在正常极限状态下的可靠度,建立正常极限状态下的功能函数方程为

2.4 计算结果及分析
2.4.1 考虑管内水压力时的计算结果 本文管线计算长度取20 m,沉陷区域长度取10 m,沉陷深度为0.3 m.采用等效弹簧[3、13]边界来代替远处管线的变形,通过命令流编程,整个计算过程都在ANSYS中进行,根据上文所述,主要分析埋地管线正常极限状态的可靠性,所以当管线的轴向最大组合应力超过496.8 MPa时就可以认为管线处于失效状态,从分析结果中可以得出,当地面沉陷位移为0.3 m,变异系数为0.1,且考虑管道内水压力置信度为95%时管线的失效概率为78.545 7%.
图4为随机采样过程中各个采样点计算出S的分布情况.图5为S的抽样过程柱状图,从中可以看出抽样过程近似服从正态分布,说明抽样的次数是满足要求的.图6为S累计分布函数示意图,通过图6可得累计分布函数趋近于1,与概率论中的相关理论是符合的.通过分析计算结果可以得到珚S=-5.063×107,σS=6.309×107,可靠度指标β=珚S/σS=-0.803.图7为灵敏度分析结果图.
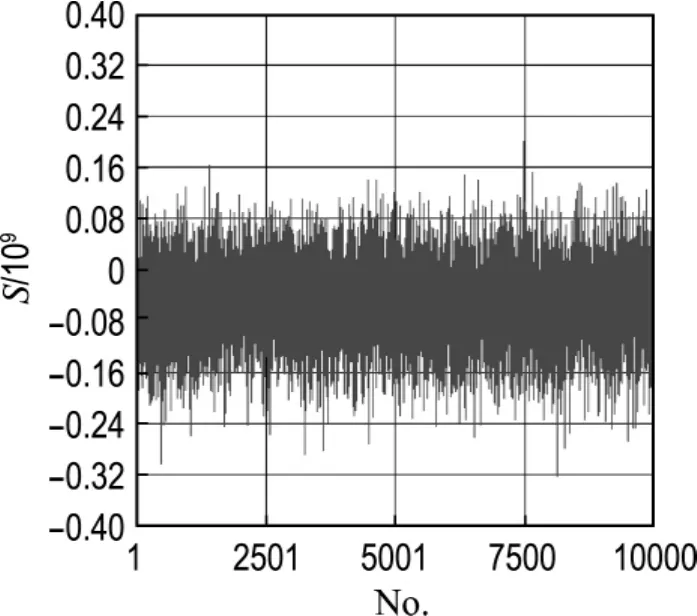
图4 考虑管内水压力时随机采样过程中各个采样点计算出的S的分布图Fig.4 The distribution of S in the random sampling process considering internal pressure in pipe
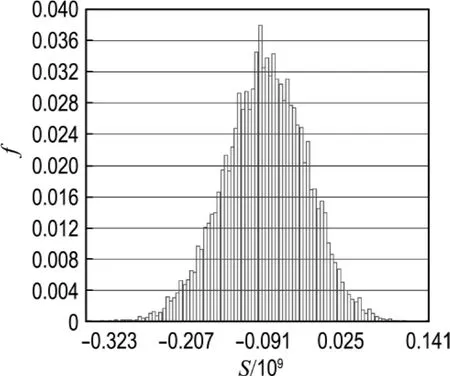
图5 考虑管内水压力时S抽样柱状分布图Fig.5 The columnar distribution of S considering internal pressure in pipe

图6 考虑管内水压力时S累计分布函数示意图Fig.6 The cumulative distribution function schematic of S considering internal pressure in pipe

图7 考虑管内水压力时灵敏度分析结果图Fig.7 The figure of sensitivity analysis results considering internal pressure in pipe
2.4.2 不考虑管内水压力时的计算结果 上节计算得出了考虑管道内水压力时埋地管线在沉陷情况下的可靠度,本节主要计算分析不考虑管道内水压力时埋地管线在沉陷情况下的可靠度.通过分析结果可以看出,当地面沉陷位移为0.3 m,变异系数为0.1,且不考虑管道内水压力置信度为95%时管线的失效概率为37.419%.
图8为随机采样过程中各个采样点计算出的S的分布情况.图9为S的抽样过程柱状图,从图中可以看出抽样过程近似服从正态分布,说明抽样的次数是满足要求的.图10为S累计分布函数示意图,通过图10可得累计分布函数趋近于1,与概率论中的相关理论是符合的.通过分析计算结果可以得到珚S=1.795×107,σS=5.385×107,可靠度指标β=珚S/σS=0.333.图11为灵敏度分析结果图.

图8 不考虑管内水压力时随机采样过程中各个采样点计算出的S的分布图Fig.8 The distribution of S in the random sampling process without considering internal pressure in pipe
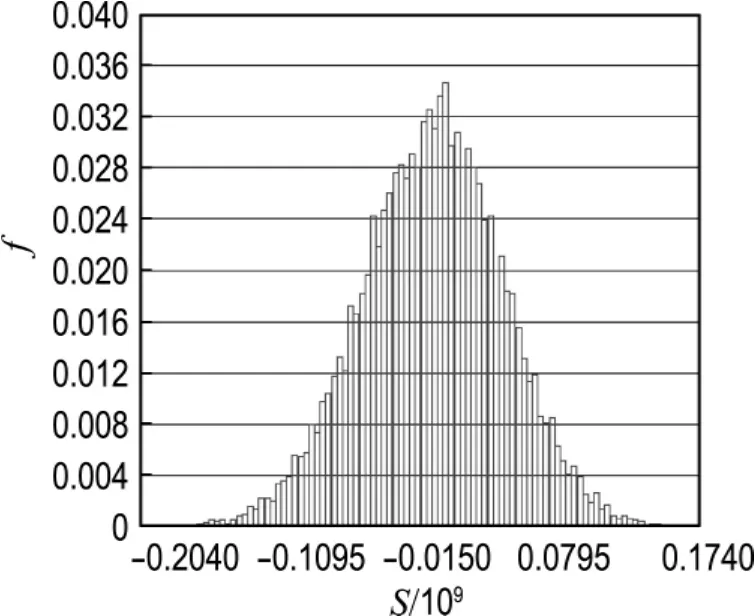
图9 不考虑管内水压力时S抽样柱状分布图Fig.9 The columnar distribution of S without considering internal pressure in pipe
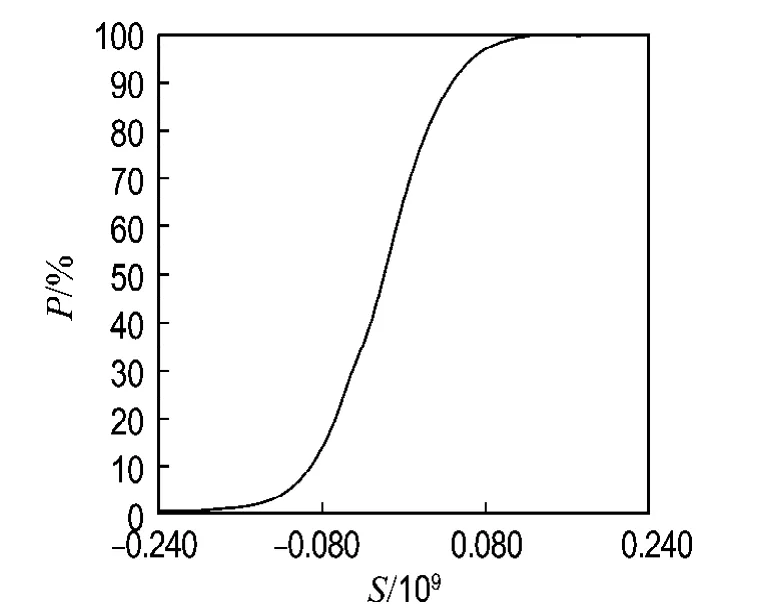
图10 不考虑管内水压力时S累计分布函数示意图Fig.10 The cumulative distribution function schematic of S without considering internal pressure in pipe

图11 不考虑管内水压力时灵敏度分析结果图Fig.11 The figure of sensitivity analysis results without considering internal pressure in pipe
3 结 论
本文主要分析研究了连续埋地管线在地面沉陷位移、管线直径、管线壁厚以及管道内水压力等随机变量下的可靠性,并采用均值一次二阶矩法和蒙特卡罗法计算了管道在这些随机变量下的可靠度,结果表明,两者计算的结果相差不大.但采用一次二阶矩法进行可靠度计算时,主要是运用概率论进行积分,难免存在误差,并且计算难度大,而蒙特卡罗法是与计算机相结合的,计算效率高且结果比较准确.地面沉陷位移的变异性对沉陷区埋地管线的可靠度有着十分重要的影响,与不考虑管道内水压力作用的结果相比,考虑管道内水压力时的失效概率较大,可靠度指标较小,管道壁厚和直径的变异性对沉陷区埋地管线的可靠度也存在着不可忽视的影响.
[1]赵国藩,金梁伟,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000
[2]高惠瑛.受场地沉陷作用的埋地管线反应分析[D].哈尔滨:国家地震工程力学研究所,1996
[3]刘爱文.基于壳模型的埋地管线抗震分析[D].北京:中国地震局地球物理研究所,2002
[4]柳春光,周 晶.管道工程系统防灾减灾讲义[M].大连:大连理工大学,2004
[5]AHAMMED M,MELCHERS R E.Reliability of pipelines subjected to corrosion[J].Journal of Transportation Engineering,1994,120(6):989-1003
[6]AHAMMED M,MELCHERS R E.Reliability estimation of pressurized pipelines subjected to localized corrosion defects[J].International Journal of Pressure Vessels and Piping,1996,69(3):267-272
[7]AHAMMED M,MELCHERS R E.Reliability estimation of pressurized pipelines subjected to pitting corrosion leaks[J].Engineering Structures,1995,17(2):74-78
[8]DAVIS P,BURN S,MOGLIA M.A physical probabilistic model to predict failure rates in buried PVC pipelines[J].Reliability Engineering&System Safety,2007,92(9):1258-1266
[9]AMIRAT A,MOHAMED C A,CHAOUI K.Reliability assessment of underground pipelines under the combined effect of active corrosion and residual stress[J].International Journal of Pressure Vessels and Piping,2006,83(2):107-117
[10]DE LEON D,MACIAS O F.Effect of spatial correlation on the failure probability of pipelines under corrosion[J].International Journal of Pressure Vessels and Piping,2005,82(2):123-128
[11]KALE A,THACKER B H,SRIDHAR N.A probabilistic model for internal corrosion of gas pipelines[C]//Proceedings of IPC 2004 International Pipeline Conference.Calgary:International Petroleum Technology Institute,2004:2437-2445
[12]PANDEY D.Probabilistic models for condition assessment of oil and gas pipelines[J].NDT&E International,1998,31(5):349-358
[13]柳春光,冯晓波.采用等效弹簧边界分析埋地管线在沉陷情况下的反应[J].地震工程与工程振动,2009,29(6):197-202
