基于Black－Scholes模型的期权定价新方法

2011-02-08沈玉波张待见宋立新

大连理工大学学报 2011年4期

沈玉波，张待见，宋立新

（大连理工大学数学科学学院，辽宁大连 116024）

0 引言

次贷危机的蝴蝶效应引发全球经济的动荡不堪.为了应付金融危机，全球性大规模联手救市展开，降息成为全球救市最直接的手段.尽管金融危机最主要的原因不是金融衍生品的定价不足，但是若整个金融市场的衍生品定价提高，则会对金融危机有所缓解，特别是应对全球金融风暴这样的突发高风险事件.

为了期权卖出者将来不再因为突发高风险事件而破产，用新的定价方法来提高价格是有必要采取的手段，为此本文延续Black－Scholes模型简单易操作且结果精确的优点，并且考虑到金融风险分布的厚尾特性，引入H k（a）＝E［（X－a）2k］（k≥1）来放大高风险突发事件在定价中的作用.

1 经典Black－Scholes模型

经典Black－Scholes模型的主要假设有［1～4］

（1）标的资产的价格服从对数正态分布，μ和σ为常数；

（2）标的资产允许卖空；

（3）不存在无风险套利机会；

（4）资产交易是连续的；

（5）没有交易费用或税收，所有资产高度可分；

（6）资产在有效期内无红利支付；

（7）无风险利率r为常数，且对所有到期日都相同.

在以上假设下，完备的概率空间（Ω，F，P）上，资产价格St模型定义如下：

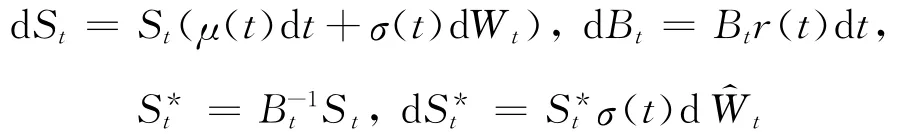
基于资产价格St的欧式看涨期权定价公式如下：

下面给出一个很重要的定理，主要用于计算过程中的测度变换.

定理1（Girsanov Theorem）［5］在完备的概率空间（Ω，F，P）上，假设

在测度P下是一个鞅，W t是（Ω，F，P）上的一个D维布朗运动，X t是D维可测适应过程且

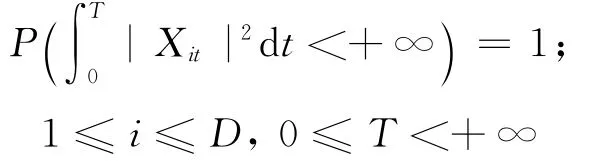
定义测度Q使得

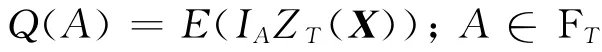
则对每一个固定的T∈［0，＋∞），W t是（Ω，F，Q）上一个D维布朗运动.

2 基于经典Black－Scholes模型的新定价方法

2.1 新方法的提出及证明

下面从数学的角度来分析一下经典的Black－Scholes模型定价公式，以欧式看涨期权为例，用X代表（ST－K）＋，E［（ST－K）＋］事实上就是函数

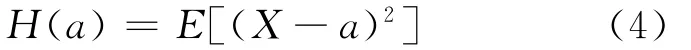
的极小值点.将式（4）一般化，利用

的最小值点ak作为期权的定价，由下凸函数的性质可以肯定这样的定价要比原定价高，但尚需通过股票指数DJSH（道琼斯上海）收益率的GARCH模型随机模拟，分别应用两个公式进行定价比较.

下面仍给市场以经典模型的假设，资产价格服从对数正态过程，分析H k（a）＝E［（X－a）2k］（k＝1，2，…）的函数性态，有

（1）H（a）＝E［｜X－a｜］时，最小值点α是X的中位数，此时尾部对α没有影响；

（2）H1（a）＝E［（X－a）2］时，最小值点β是EX，尾部对β产生影响；

（3）H k（a）＝E［（X－a）2k］，a≥0，k＝1，2，…时，假设EX2k＜＋∞，由控制收敛定理［6、7］可推得H k（a）＝E［（X－a）2k］关于a可导，由

可知H k（a）＝E［（X－a）2k］在正半轴上有唯一的最小值点ak.换个角度来说ak为方程H′k（a）＝－2kE［（X－a）2k－1］＝0的实根，即E［（X－a）2k－1］＝0的实根.

由以上判断可知：正半轴上根是唯一的，当a＜0时，H′k（a）＝－2kE［（X－a）2k－1］＜0恒成立，所以方程无负实根.综上H′k（a）＝0有唯一的正实根ak.这样就可以用ak作为期权的定价.

资产价格服从模型仍是

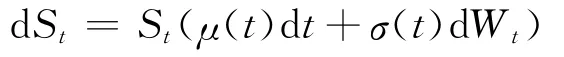
这样就可以得到其导数的表达式，但是比较复杂，下面具体就k＝2时进行分析.H2（a）的导数为三次多项式，由三次方程的公式解可得卡尔丹公式x3＋px＋q＝0的解为

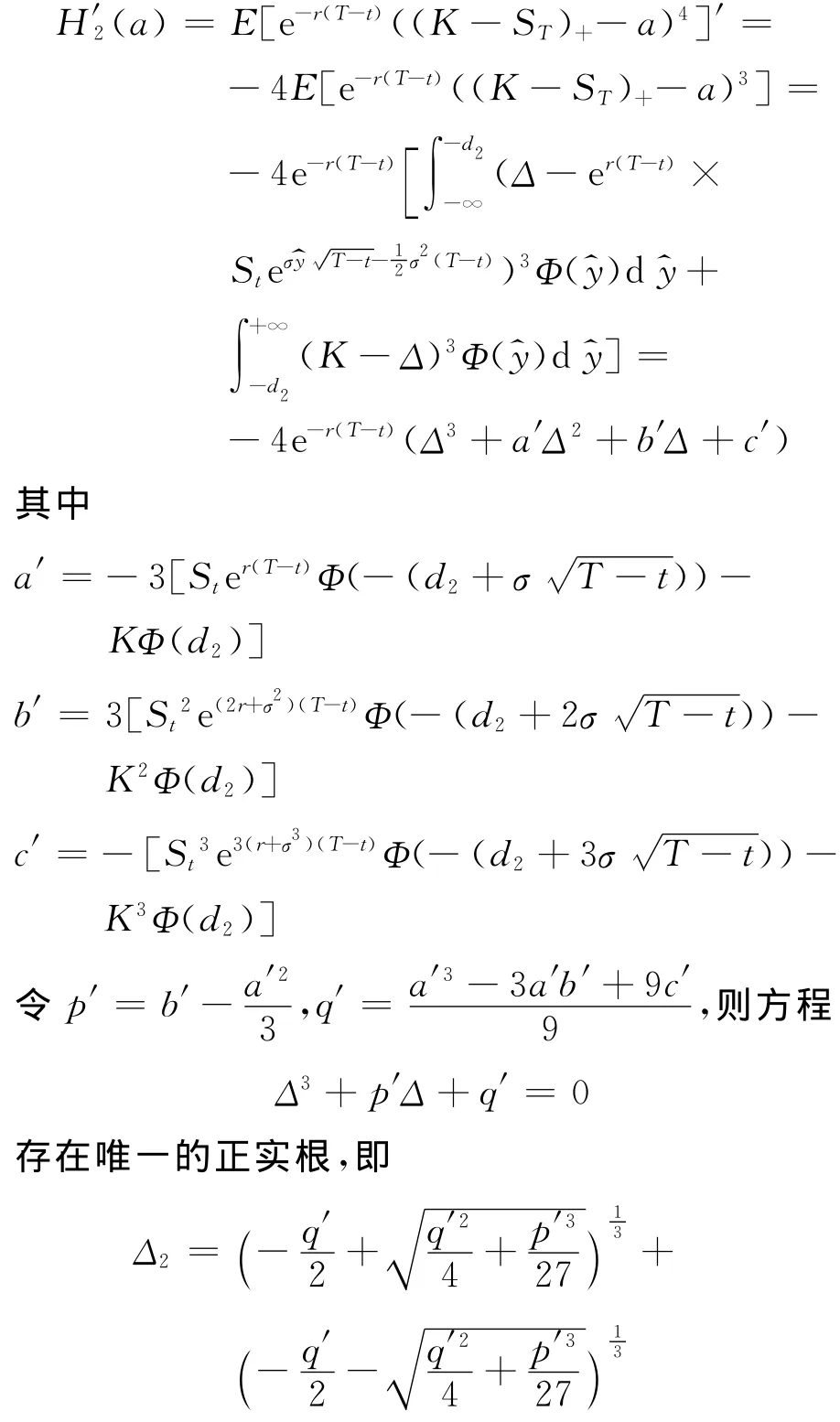
从而看跌期权的定价为

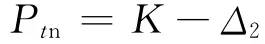
2.2 新方法下看涨－看跌期权平价关系

对于两个相同有效期T－t，相同敲定价格K的欧式看涨和看跌期权有平价公式

新定价的欧式看涨－看跌期权平价关系为

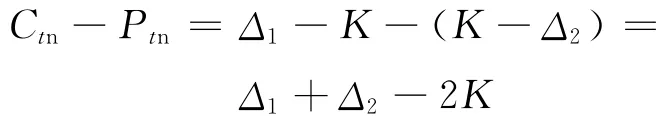
3 随机模拟

对于定价新公式，可以选择不同的k，随着k的增大，突发事件的放大作用也增大，这正是所想要的结果.本文以k＝2为例，采用随机模拟的方法［8］，以两年期的DJSH指数的欧式看涨期权为例，分别使用Black－Scholes公式和基于Black－Scholes模型的新定价公式为它定价并进行比较.

GARCH模型一定程度地反映现实市场的不完备性，并且运用计量经济软件Eviews可以很方便地得到，因此采用DJSH（2006～2009）的数据，用GARCH（1，1）模型对DJSH指数的对数日收益率建模.用估计好的对数日收益率的GARCH（1，1）模型模拟出DJSH指数的1 000个日价格，然后对基于该指数的两年期欧式看涨期权进行定价.

设定常用的无风险年收益率r＝0.05，T＝720 d，即2 a，选择两个执行价格K1＝276.00，K2＝278.00，分别用式（5）和经典Black－Scholes模型进行定价，计算得到定价的平均价格和价格的标准差，为了明确比较，列成表1.