基于广义Nakagami分布的医学超声图像去斑点噪声算法

侯建华，朱淑琴，陈少波

(中南民族大学电子信息工程学院，武汉430074)

在医学临床诊断中，超声图像与其他医学图像相比具有非侵入式、使用方便、成本低、对人体损害小等优点.由于成像机制的限制，超声图像存在固有的斑点噪声，它极大地降低了图像的质量，使得正常组织和肿瘤病变组织不易被区分.因此，斑点噪声的抑制在医学超声图像预处理过程中是具有非常高的研究价值和应用前景.

常用的超声图像斑点抑制的算法主要有:均值滤波、中值滤波［1］、Jain 提出的同态维纳滤波［2］等.基于斑点噪声的局部统计特性，一些学者研究了自适应的低通滤波器，如 Lee滤波器［3］，Kuan滤波器［4］，Loupas提出的自适应权系数中值滤波［5］等.这些算法的共同点是取一个滑动窗对图像进行滤波处理，因此滤波后图像细节的分辨率很差.

小波变换良好的时频特征和多尺度特性成为图像去噪的一个强有力的工具.根据超声图像斑点噪声的乘性特点，通常先对含斑噪图像进行对数变换，将乘性噪声转变为近似的加性高斯白噪声，然后利用常规的小波去噪技术对系数进行修正.在对数变换和冗余小波变换的框架下，本文选用双边广义Nakagami模型［6，7］、高斯模型分别描述斑噪小波系数和信号小波系数，利用最大后验概率准则对每个高频子带的小波系数进行斑点抑制.

1 斑噪与信号的小波系数统计模型

首先建立噪声模型，超声图像一般使用乘性模型描述:

其中y，x分别代表含斑信号和无噪信号，n为乘性斑点噪声随机变量，且与无噪信号相互独立.

对(1)式取对数变换，将乘性噪声转变为近似的加性高斯白噪声:

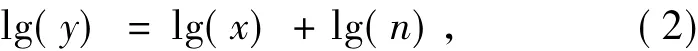
为了简便，公式(2)可写成:

1.1 斑点噪声的小波系数统计模型

很多统计模型都能描述不同散射信号情况下斑点噪声的特性，包括最常用的瑞利分布以及非瑞利分布，如K分布，Weibull分布，Nakagami分布等.本文采用双边广义Nakagami分布能够更好的描述超声图像各层子带的斑噪小波系数的统计特性，其概率密度函数(pdf)［6，7］如下:

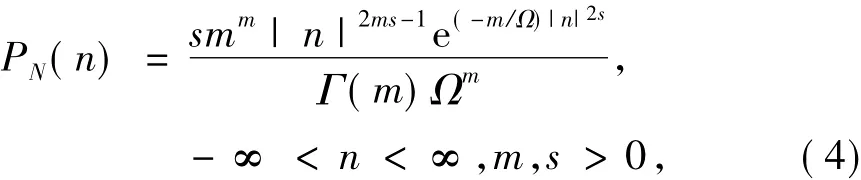
其中:

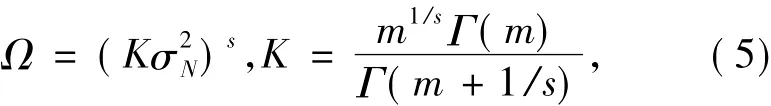
其中σ2N(σN＞0)是斑噪小波系数N的方差，s是形状调节参数，m是Nakagami参数，噪声能量Ω决定了函数衰减的速度.而参数m和s可以由最大似然估计法从各个高频子带系数求得:

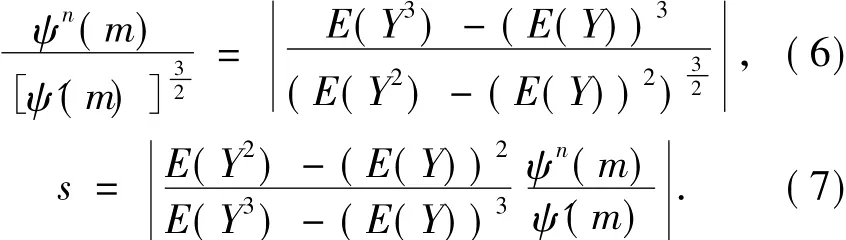
函数ψ(v)是以v为变量的双伽马函数，v可由(8)式求得:

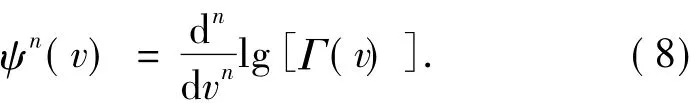
1.2 信号的小波系数统计模型

很多学者已经指出自然图像的小波系数直方图呈现出很长的重拖尾并且在零点处出现急剧的尖峰.基于这种分布特性，本文采用均值为0的广义高斯分布(GGD)对信号小波系数建模.GGD的概率密度函数［8］如下:

其中:

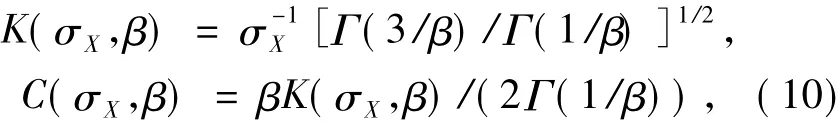
高斯分布是当β=2时GGD模型的特例，其概率密度函数为:

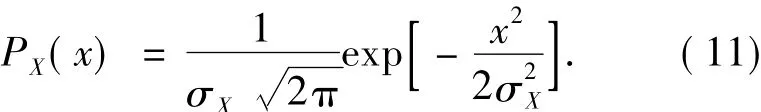
2 基于Bayes估计的去斑算法

2.1 基于MAP的Bayes估计

在贝叶斯估计理论中，给出观测信号Y，那么信号X可以由最大后验概率估计(MAP)求得:

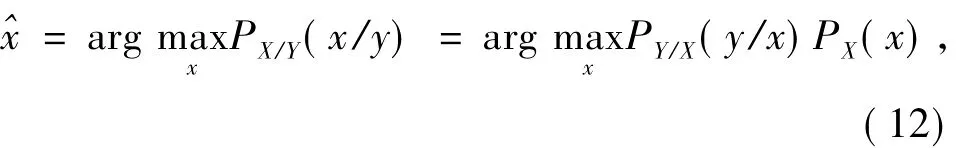
公式(3)代入，可得:

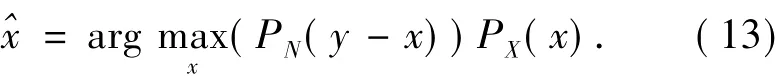
斑噪小波系数建模为双边GND，信号小波系数建模为高斯密度函数，即公式(4)和公式(11)代入公式(13)可得:

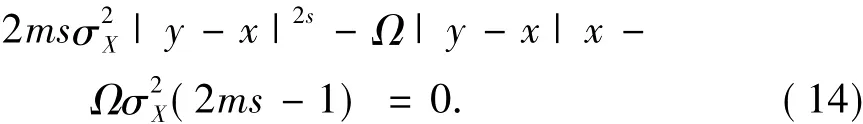
则可推出:

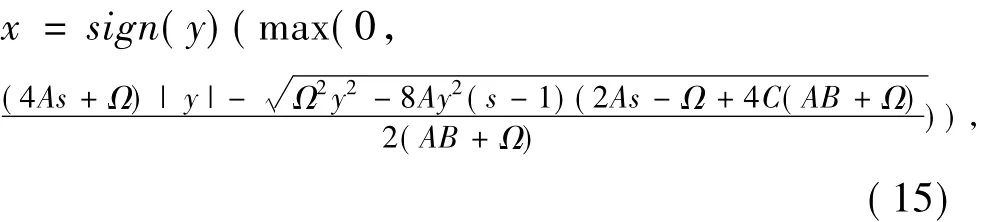
其中A=msσ2X y2s－2，B=2s(2s－1)，C=(2ms－1)ΩσX，公式(15) 被称为 GNDShrink.

2.2 模型参数的估计

斑点噪声方差 σ2N用 Donoho［9，10］提出的鲁棒性中值定理求得:

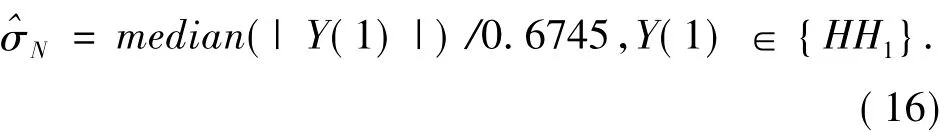
由于X和N都是独立随机变量且均值为0，故有:

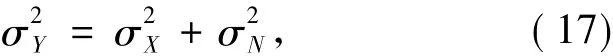
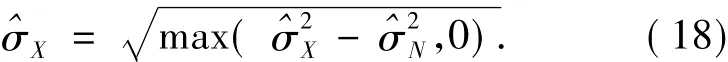
那么可以得到模型边缘标准差:是含噪子带的方差估计，可由(19)式得到［6］:

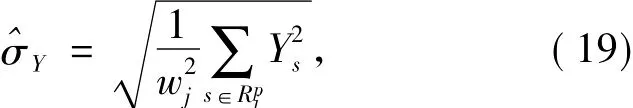
其中，Rpj是以p为中心以wj×wj为大小的滑动窗口，窗口大小wj是根据图像分解层数来定义的，例如最高层的系数方差很大时选择较小的滑动窗可以有效的去除噪声，粗糙层的系数方差很小时选择较大的滑动窗可以保存更多的图像细节.所以窗口大小可以由图像分解层数j计算得出:

其中，t1是最高层的滑动窗口，尺寸大小为3×3.

3 本文算法步骤

由于正交离散小波变换(DWT)不具备平移不变性，容易使去噪后的图像出现振铃效应和伪Gibbs效应，所以本文采用冗余小波变换(RWT)，虽然它的计算量有所增加，但是可以显著的提高图像去噪质量.

基于广义Nakagami分布的去斑点噪声算法步骤如下:

⑴对含斑点噪声图像作对数变换后进行冗余小波分解;

⑵根据公式(16)估计噪声方差^σN;

⑶除低频子带外，对每个高频子带:

(i)由公式(5)～(8)计算出每个子带的形状调节参数s，Nakagami参数和噪声能量Ω;

(ii)根据公式(18)～(20)估计模型边缘标准差^σX;

(iii)根据公式(15)对当前系数进行处理;

⑷进行冗余小波反变换(IRWT)后作指数变换可得到去噪后的图像.

4 性能评估

4.1 去斑噪声算法客观评价指标

去斑噪算法的客观评价指标，可以从这几个方面来衡量:保留细节、边缘以及纹理的能力.本文中选用以下两种方法［6］.

⑴信噪比(SNR).

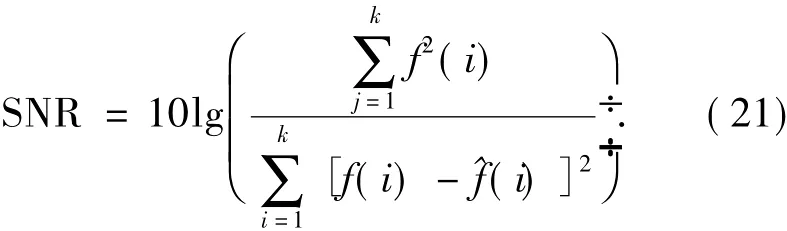
其中，f为原始图像，^f为去斑噪后图像.SNR越大说明去噪效果越好.

(2)相关系数(CoC).

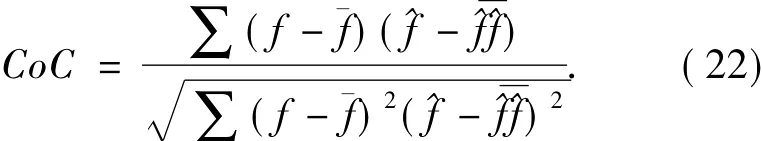
4.2 实验结果及分析

实验图像选用合成的无斑噪超声图像，如图1(a)所示，人为地加上斑点噪声后，用Daubechies4小波作4尺度的冗余小波分解，通过以下5种算法进行比较:均值滤波，Lee 滤波［3］，同态维纳滤波［2］，BayesShrink软阈值去噪算法［8］和GNDShrink算法.

从表1中可以看出，对人工合成无斑噪超声图像分别加噪声标准差为0.6和0.9的斑点噪声时，GNDShrink算法在信噪比SNR和相关系数CoC的客观评价指标均优于其他4种算法.均值滤波，Lee滤波［3］，同态维纳滤波均属于空域滤波方法，其本质是低通滤波;BayesShrink软阈值去噪算法和GNDShrink算法属于时域滤波方法，利用子带领域系数的相关性，对小波系数进行建模，去噪效果比较明显，尤其是本文提出的算法滤波后的信噪比和相关系数都得到了很大的提高.

图1是噪声标准差为0.6时以上5种方法对人工合成斑点噪声图像去噪后的对比.图2(a)选用的是大小为的真实带斑点噪声超声图像，图2(b)-(g)用以上5种算法对其进行去噪处理后得到的图像.从主观视觉上可以看出，均值滤波、Lee滤波、同态维纳滤波和BayesShrink软阈值去噪算法虽然滤除了斑点噪声，但造成图像过多细节的丢失;GNDShrink算法与另外4种算法相比，在有效地抑制斑点噪声的同时，能更多地保留图像的纹理和边缘.

图1 (σ=0.6)各种去斑算法的主观视觉效果比较Fig.1 Subjective visual comparison of various despeckling algorithm

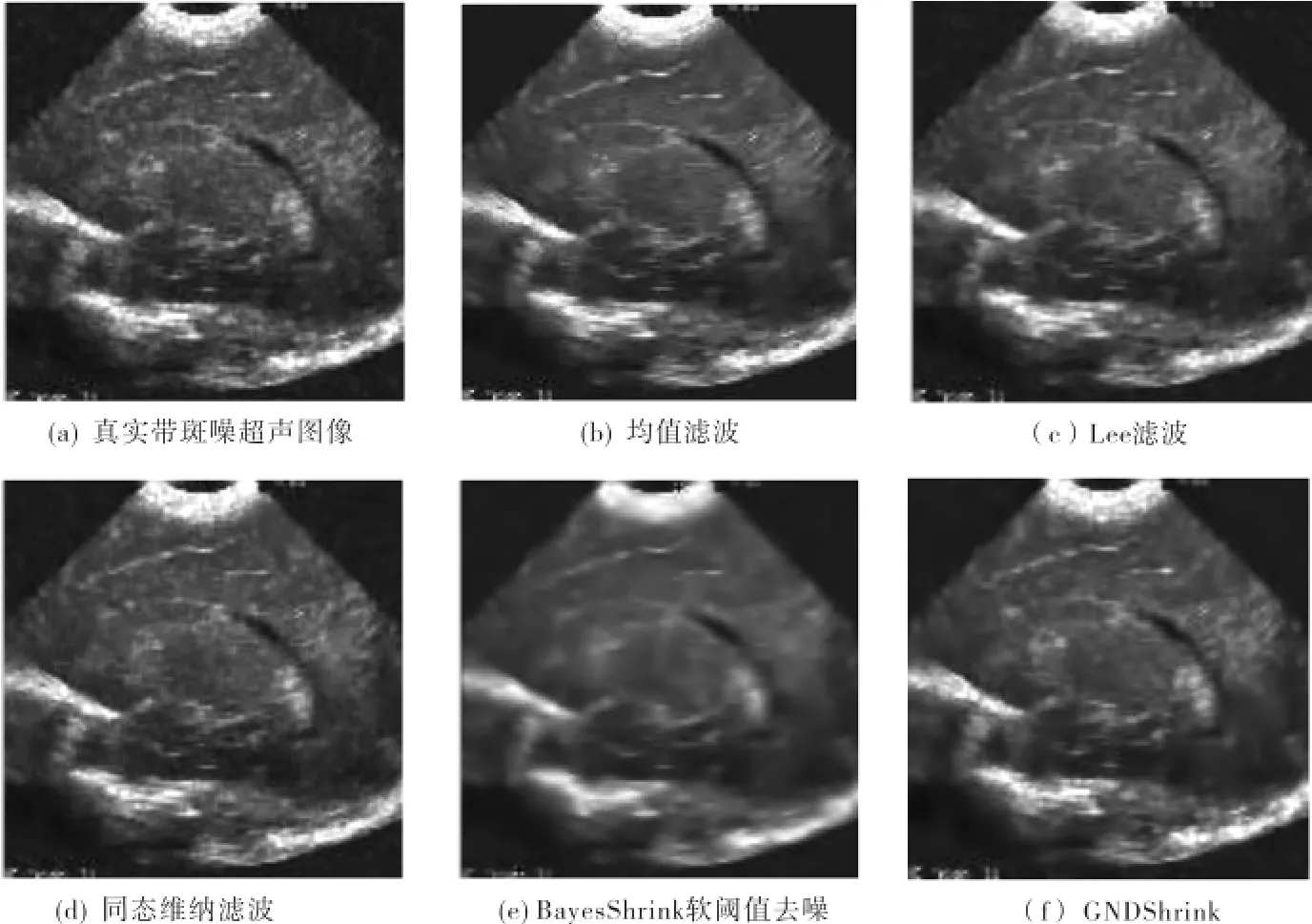
图2 各种去斑算法的主观视觉效果比较Fig.2 Subjective visual comparison of various despeckling algorithms

5 结语

本文实现了一种具有自适应性的去斑噪算法.首先，对含斑噪图像进行对数变换和冗余小波分解变换，然后分别用广义Nakagami模型描述斑噪小波系数的统计特性，用高斯模型描述子带中的信号小波系数统计特性，最后利用贝叶斯最大后验概率估计准则推导出该算法.通过人工合成加斑噪图像以及真实含斑噪图像的客观评价指标和主观视觉上的对比，该算法比另外4种算法都能更多地保留图像的纹理和边缘.

［1］Chen M S，Han J.W，Yu P S.Data mining:an overview from a database perspective［J］.IEEE Transactions on Knowledge and Data Engineering，1996，8(6):866-883.

［2］Jain A K.Fundamentals of digital image processing［M］.Englewood Cliffs:Prentice Hall，1989.

［3］Lee JS.Refined filtering of image noise using local statistics［J］.Computer Graphic and Image Processing，1981，15(1):380-389.

［4］Kuan D T，Sawchuk A A，Strand T C，et al.Adaptive noise smoothing filter for images with signal-dependent noise［J］.IEEE Trans Pattern Analysis and Machine Intelligence，1985，7(2):165-177.

［5］Loupas T，McDicken W N，Allen P L.An adaptive weighted median filter for speckle suppressin in medical ultrasonic images ［J］.IEEE Trans Circuits Systems，1989，36(1):129-135.

［6］Gupta S，Kaur L，Chauhan R C，et al.A versatile technique for visual enhancement ofmedical ultrasound images［J］.Digital Signal Processing，2007，17(3):542-560.

［7］Shankar P M.Ultrasonic tissue characterization using a generalized Nakagamimodel［J］.IEEE Trans Ultrason Ferroelectr Frequency Control，2001，48(6):1716-1720.

［8］Chang G，Yu B，Vetterli M.Adaptive wavelet thresholding for image denoising and compression［J］.IEEE Trans Image Proc，2000，9(9):1532-1546.

［9］Donoho D L，Johnstone I M.Ideal spatial adaptive via wavelet shrinkage［J］.Biometrika，1994，81(3):425-455.

［10］Donoho D L，Johnstone I M.Adapting to unknown smoothness viawavelet shrinkage［J］.Journalof the A-merican Statistical Assoc，1995，90(12):1200-1224.