含奇异项的脉冲抛物型方程猝灭时间的控制

孙仁斌

(中南民族大学数学与统计学学院，武汉430074)

对于脉冲常微分方程的研究已有不少成果，而对于含有扩散的脉冲微分方程的研究也日益受到人们的关注．早期的工作见文献［1］，他们考虑脉冲抛物型方程的初边值问题，建立了极大值原理与比较原理，并对解的稳定性进行了讨论．此后，对于脉冲抛物型方程解的各种性质的文献日渐增多，一些重要的结果见文献［2］-［7］．

本文考虑如下含有奇异项的脉冲抛物型方程的初边值问题:

这里Ω是Rn中一有界开区域，具有光滑边界∂Ω，t1，t2，…，tm与T是一组给定的正数，满足

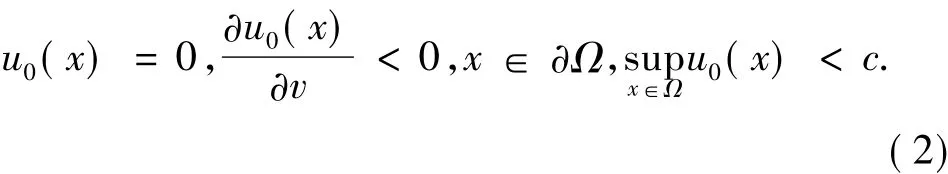
其中v是∂Ω上的单位外法向量．

关于问题(1)的解的定义及解的存在与唯一性，与文［8］中类似，此处不再重复．

定义如存在有限正常数T，使问题(1)的解满足，就称解u(t，x) 在有限时刻T猝灭．

对含奇异项但没有脉冲的抛物方程初边值问题，已有的结论是当Ω充分大时，解会在有限时刻猝灭，当Ω适当小时有整体解存在［9］．本文的工作是通过构造上下解对脉冲源和反应函数进行控制，使相应解的猝灭时刻延迟，使之达到预定的时段内．

1 上下解的构造

问题(1)上下解的定义可参考文献［8］．下面的引理1是已有的结论．

引理1设λ1与φ(x)是如下特征值问题的第一特征值与相应的特征函数:

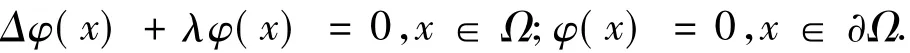
则λ1＞0，且当x∈Ω时，φ(x)＞0，φ(x)可规范化，使之满足我们容易证明下面的引理2．

引理2设α是一正常数，g(z)=z(c－z)α，则当时，g(z)单调不减，且在(0，c)内g(z)的最大值为:

为得到本文的结果，我们引入如下2个假设．

H1设f(t，x，η)∈C1(QT×R)，且存在正常数α，b和B，使得当时，下面的不等式成立:

H2设脉冲源函数Ik(u)，(k=1，2…，m)是单调不减的连续函数，且存在正数ak与Ak满足ak≤Ak＜1，使得当η≥0时有:

这里ak与Ak起着控制脉冲源Ik的作用．

下面构造问题(1)的上下解，先构造下解．首先从条件(2)，我们能够取一常数p0满足0＜p0＜且:

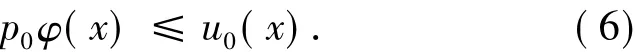
令E1=(1+α)b，

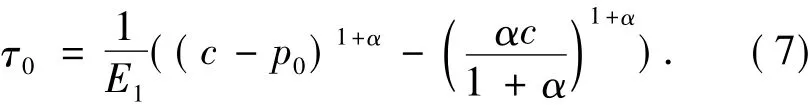
则τ0＞0，假设t1满足:

当t∈ (t0，t1) 时，定义:

则有p(t+0)=p0，p(t) ≥p0，且:

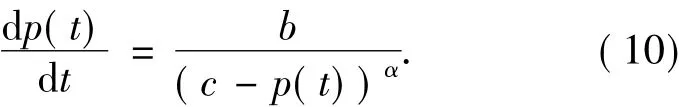
由(7)式可得:

其次，对k=1，2，…，m－1，我们按归纳的方式依次定义τ1;t2;p(t)，t∈ (t1，t2);p2;…;τk;tk+1;p(t)，t∈ (tk，tk+1);… 如下:

假设tk+1满足0＜tk+1－tk＜τk，当时定义令:

则pk=p()，且p(t)满足方程(10)和不等式(11)，因此并且由ak＜1有 τk＞0．

最后，令pm=am p()，当k=0，1，2，…，m－1 时，令:

引理3设H1，H2成立，u0(x)满足(6)式，那么由(14)、(15)式定义的函数u(t，x) 是问题(1)的一个下解．

证明对k=0，1，2，…，m－1，当t∈ (tk，tk+1)，x∈Ω时，利用引理1和(10)式，有:

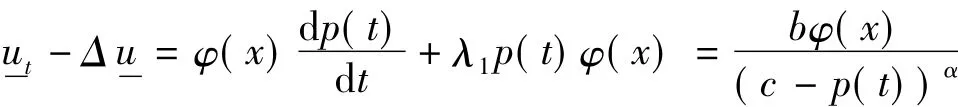
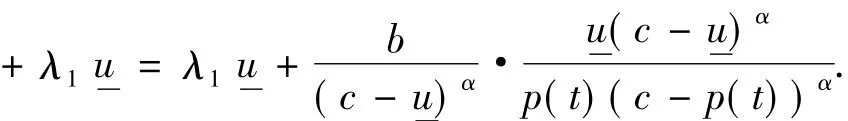
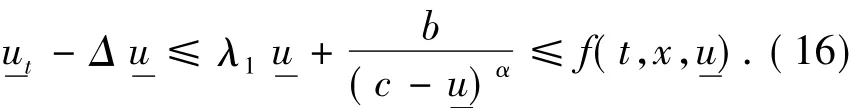
当t∈ (tm，T)，x∈ Ω 时，从(15)式知不等式(16)成立．

下面构造问题(1)的上解，为此设:

首先，令E2=(1+α)(B+λ1M)，其中M由(3)式给出，易知0，设t1满足:

与构造下解时类似，当t∈(t0，t1)时，定义:

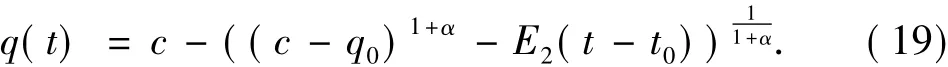
则有q(t+0)=q0，q(t)≥q0，且q(t)满足:

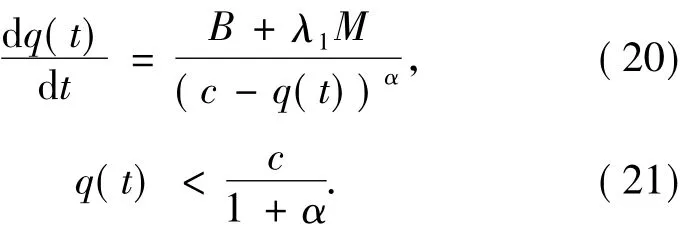
其次，对k=1，2，…，m－1，按归纳的方式定义:

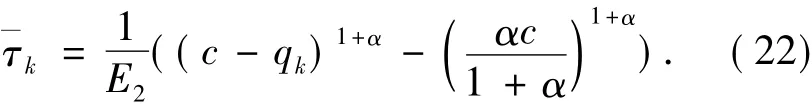
设tk+1满足:

当t∈(tk，tk+1)时定义:

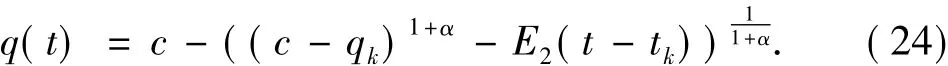
结合(19)、(24)与(25)式定义:

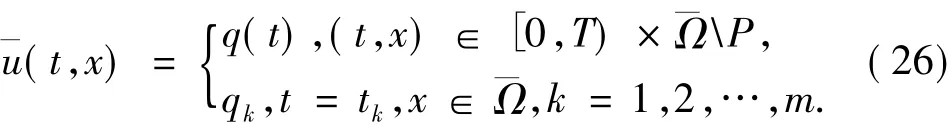
引理4设H1、H2与(17)式成立，则由(26)式定义的函数是问题(1)的一个上解．

证明显然，(t，x) ∈［0，T)×∂Ω 时，有，当x∈ Ω 时．当x∈Ω，k=0，1，2，…，m. 由 H2 可得，当(t，x)∈QTP，由(21)式、引理2与 H1，有:

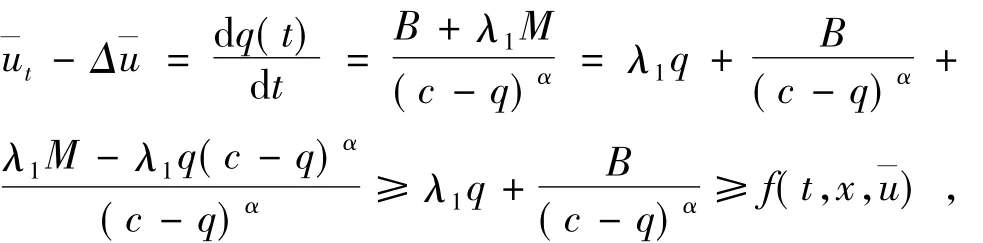
证毕．

2 猝灭时间的控制

定理 1设 H1、H2成立，u0(x)满足(6)与(17) 式，t1满足(18)式，且k=1，2，…，m－1时tk+1满足(23)式，则问题(1)的解u(t，x)在有限时刻猝灭，且猝灭时刻T*满足T1≤T*≤T2．

证明设u(t，x)是问题(1)的解，y(t)=则由比较原理有:

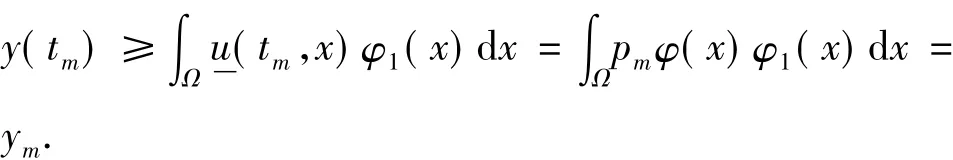
在问题(1)的方程两边乘以φ1(x)，关于x在Ω上积分，得到:

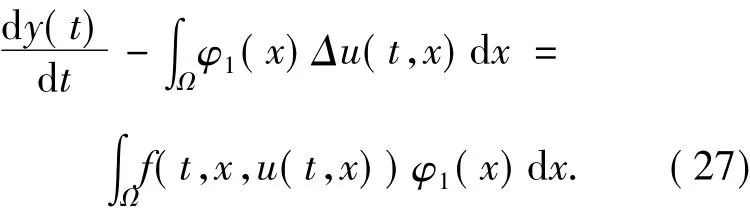
利用边界条件、H1及Jensen不等式可得:

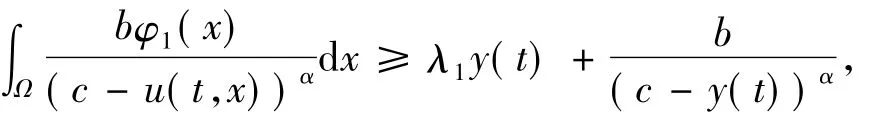
令tm＜t＜T，关于t对上面的不等式在［tm，t］上积分得:

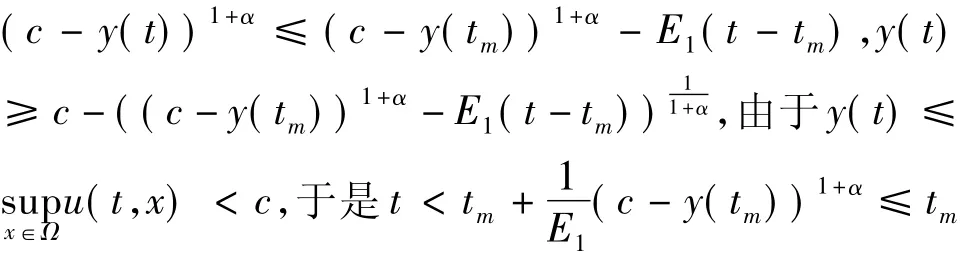
为了得到T*的下界，由(25)式有c，既然显然有因此T*≥T1，证毕．

［1］Erbe LH，Freedman H I，Liu X Z，et al．Comparison principle for impulsive parabolic equationswith applications to models of single species growth［J］．J Austral Math Soc Ser B，1991，32:382-400．

［2］Chan C Y，Ke L，Vatsala A S．Impulsive quenching for reaction-diffusion equations［J］．Nonlinear Analysis，1994，22:1323-1328．

［3］Bainov D D，Kolev D A，Nakagawa K．The control of the blowing-up time for the solution of the semilinear parabolic equation with impulsive effect［J］．JKorean Math Soc，2000，37:793-803．

［4］Fu X L，Liu X Z，Sivaloganathan S．Oscillation criteria for impulsive parabolic differential equationswith delay［J］．J Math Anal Appl，2002，268:647-664．

［5］Gao W L，Wang JH．Estimates of solutions of impulsive parabolic equations under Neumann boundary condition［J］．JMath Anal Appl，2003，283:478-490．

［6］Lovane G，Kapustyan A V，Valero J．Asymptotic behaviour of reaction-diffusion equationswith non-damped impulsive effects［J］．Nonlinear Analysis，2008，68:2516-2530．

［7］Chan C Y，Kong P C．Impulsive quenching for degenerate parabolic equation［J］．JMath Anal Appl，1996，202:450-464．

［8］孙仁斌，胡军浩．脉冲抛物型方程解的爆破时间的控制［J］．云南大学学报:自然科学版，2007，29(1):16-19．

［9］DaiQ Y ，Gu Y G．A shortnote on quenching phenomena for semilinear parabolic equations［J］．J Differential Equations，1997，137:240-250．