电动汽车充电器直流滤波器的设计

康伟 张翮 陈兴 詹广兴 王钰 张丽霞

(1.中国石油大学 信息与控制工程学院，山东东营 257061;2.河南省电力公司南阳供电公司，河南南阳 473000)

0 引言

目前动力汽车充电器主要是相控方式和PWM方式的整流器［3］。其结构如图1所示。动力蓄电池组是等容性的特殊负载，其内阻极小，本身具有反电动势。即使充电器输出电压纹波较小，充电电流也会有较大的纹波。假设充电器输出的电压为Uo，电池组反电动势为Eo，内阻为ro(ro≪1Ω)，则电池组的充电电流Io=(Uo－Eo)/ro。因此即使整流器输出电压纹波合格，电流也可能存在较大的纹波，因而必须在直流侧设置滤波器，以减少充电电流的谐波含量，延长电池组的使用寿命。

图1 电动汽车充电器结构

针对以上问题，论文基于电流纹波抑制，快速响应性的提高以及滤波器匹配型设计三个方面对动力汽车充电器滤波器的设计展开讨论，并通过方针和试验验证了方案的合理性和可行性。

1 低纹波滤波器的设计

1.1 滤波器的算法

电池组充电首要问题是减小充电电流的纹波。但是电池组的反电势和小内阻为滤波器设计带来了困难。此外，因为整流器输出的电压纹波和电流纹波都是6次及以上高次谐波［4］，通带(直流)和阻带(6次谐波)间隔较近，要尽量提高过渡带衰减的增长速度，以达到合适的滤波效果。根据低通滤波器不同的衰减特性，形成的滤波器主要有以下几种［5］:最平响应滤波器，切比雪夫滤波器，考尔参数滤波器和一般参数滤波器。

巴特沃斯滤波器在通带内有较为平坦的滤波特性，阻带内的衰减随频率单调增大;切比雪夫滤波器在通带内呈现等起伏特性，而阻带内的衰减具有更快的增长速率;考尔参数滤波器在通带和阻带内衰减都呈现等起伏特性;一般参数滤波器在通带内作等起伏变化，在阻带内可以按照设定的规律变化。切比雪夫滤波器在通带内有等起伏特性且阻带内的衰减有较高的增长速率，并且较易于实现，其衰减特性，十分符合动力蓄电池组测试系统直流侧滤波器设计的需要。因此，论文设计了基于切比雪夫滤波器的直流滤波器。

按照传统理论，切比雪夫滤波器的阶数n应该满足公式(1)

其多项式的一般形式为

1.2 滤波器匹配特性的讨论

设计滤波器必须考虑其匹配特性。当假定滤波器两端所接阻抗相等时，称之为匹配的;如假定不相等，称之为非匹配的。通常讨论的滤波器设计都是基于匹配型滤波器的设计。但是对于动力汽车充电用的直流滤波器来说，其一侧接的是电网，另一侧为蓄电池组。因为电动汽车用电池组是由多节电池串并联组成，而电池组的内阻不是一个固定的数值。不同材质的电池内阻不同［5］，一般来说，铅酸电池的内阻要大于锂离子电池和金属氢化物(MH-Ni)电池。(MH-Ni电池内阻为0.23mΩ左右)，超级电容器更小;而同一材质的电池，容量越大，内阻越小;同一节电池，内阻会随着使用的次数的增加略呈增大的趋势。

因为我国配电网的特殊性，系统阻抗远大于电池组的阻抗，所以动力汽车充电器的直流滤波器要按照非匹配型设计［6］。如果滤波器为非匹配型(即滤波器两端系统等校内组不相等)，会为滤波器的传输特性在匹配型上增加平坦衰减［7］;如果非匹配型的滤波器按照匹配型的设计，会大大影响其滤波效果［7］。

隧道排烟设计，考虑排烟区段较长，隧道设排烟竖井一座，设置在桩号K104+439与K104+430左右线中间处，竖井井口标高926 m，井深88 m，成井直径5.20 m，最大开挖直径6.52 m(包含5 cm预留变形量)，距离右线出口761 m。两隧道均设置排烟横洞与之连接。竖井正常情况下不启用，仅在火灾情况下视火灾发生的不同部位结合防灾预案正确开启来排烟，排烟区段分4 900 m和800 m两个区段排烟。

因为匹配型和非匹配型滤波器只是参数不同而拓扑结构完全相同，所以二者拓扑结构统一如图2所示。

图2 五阶切比雪夫滤波器结构

参照文献［6］，论文选取滤波器的阶数为5阶。因为切比雪夫滤波器的衰减特性为通带内有小量起伏，设计滤波器时将通带内衰减设大，可以在某种程度上抑制低于6次的谐波［9］。按照切比雪夫多项式，当 Ap=8，ω=200π，内阻为0.2 Ω 设计匹配型和非匹配型切比雪夫滤波器参数分别如表1和表2所示。

1.3 匹配型滤波器和非匹配型滤波器仿真比较

因为相控方式的整流器输出谐波含量远大于PWM方式，因此论文仅选取相控方式的整流器进行比较分析。根据图1所示的结构分别搭建充电系统，将匹配型滤波器和非匹配型滤波器，分别接入系统进行滤波，整流桥滤波前、经匹配型滤波器滤波和非匹配型滤波器滤波的电流波形如图3(1)～3(3)所示。仿真系统参数如下:三相峰值电压50V，电池组内阻0.2Ω，反电动势38V，触发角 α=40°，滤波器参数参考表1，表2。

表1 匹配型切比雪夫滤波器参数

表2 非匹配型切比雪夫滤波器参数

由仿真结果可以看出，非匹配型滤波器考虑了负载的大小差异，因此滤波效果要优于匹配型滤波器的滤波效果。但是其响应速度仍然比较慢，因此应采取措施提高系统的响应速度。

2 提高滤波器响应特性方法

针对论文设计的切比雪夫滤波器，目前有三种方法可以用来提高滤波器的响应速度，因为对他们没有统一的称呼，论文在此简称为谐振法、阻尼控制法和极点分析法，将他们的原理应用于论文设计的滤波器，并比较如下。

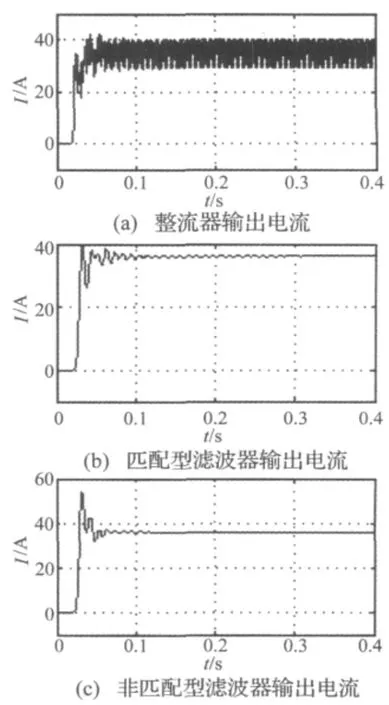
图3 匹配型和非匹配型滤波器滤波比较

2.1 谐振法

谐振法改进的滤波器是通过在滤波器并臂(即并联电容的臂)串入电阻，让该臂的并联谐振频率等于需要滤除的谐波，因为对滤波器的传输特性影响较大，所以电阻应串入滤波电流相应较小的臂［10］。由仿真可知，流过电容C2的电流远小于C1的电流(限于篇幅本文不给出波形)，因此电阻应与C2串联。根据谐振法的原理，其拓扑结构如图4所示。

图4 谐振法修正的滤波器结构

修正后的滤波器参 数 为 L1= 0.0012H， L2= 0.0015H，L3=0.0012 H，C1= C2=5900μF，R=0.28Ω。

2.2 阻尼控制法

阻尼控制法［11］的原理是将多阶滤波器分解成若干简单Γ型滤波器级联的形式，然后通过分别控制他们相应的阻尼比达到提高响应速度的目的。修正后的滤波器结构如图5所示。

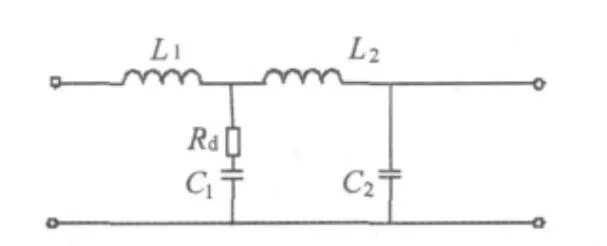
图5 阻尼控制法修正的滤波器结构

滤波器被分为两级，L1，R1和 C1组成的初级和 L2，C2组成的次级谐振电路，F0是整流器输出谐波频率，两级电路的截止频率分别为F1，F2。根据阻尼控制原理，针对公式

为了限制 F2的谐振峰值，应，20lgpP2＜0，L2/L1＜1，通常L2/L1=0.25H ～0.6H，C2/C1应该尽量小，通常 C2/C1=0.05 ～0.1，修正后的滤波器参数为 L1=0.0012H，L2=0.0006H，L3=0.0012H，C1=5900μF，C2=3000μF，Rd=1Ω。

2.3 极点分析法

极点分析法［12］修正后滤波器结构同图5，根据文献［7］，修正前的切比雪夫滤波器的极点分布于一椭圆上。并臂加入电阻后，滤波器的极点位置发生了变化，但是为了尽量维持滤波器的传输特性，新的极点应尽可能接近原来的位置。5阶滤波器在C1处串联电阻Rd后系统的转移导纳YT(s)为

提高系统的响应速度即提高YT(s)的曲线的响应速度。

修正后的滤波器参数为 L1=0.0012H，L2=0.0015H，L3=0.0012 H，C1=C2=5900μF，Rd=0.6Ω。

2.4 仿真验证

基于MATLAB搭建图1所示的三组电池组充电系统，分别取三种方法修正滤波器的结构和参数。选取控制角α=40°，此时对应整流桥输出电压谐波较严重的情况(输出电压谐波含量达到60%)。相控整流桥输出电流经滤波后波形如图7(a)～7(c)所示。当滤波器都进入稳态后，取0.4s～0.42s的电流进行FFT分析，则图7中(a)，(b)，(c)对应的谐波含量分别为0.2%，2%和0.4%。从响应速度分析，7(a)、7(b)、7(c)对应的响应时间分别是 0.12s，0.04s，0.06s.

图6 三种快速响应算法仿真比较

由仿真结果可以看出，阻尼控制法能够迅速提高滤波器的响应速度(响应时间为其它方法的一半)，但是因为对元件参数修正过多，因此滤波效果明显受到影响，因此输出电流纹波过大，因而这种方法适合对响应速度严格要求而对输出电压或电流纹波要求较宽松的场合(如不具备反电动势的负载等)。而谐振法和极点分析法的滤波效果明显要好的多。如果改变控制角α，则谐振法在充电电流较大(即α较小时)，与极点分析法相比，系统具有较长的响应时间(限于篇幅，文中未给出比较波形)，因此，使用极点分析法修正切比雪夫滤波器，应用于电动汽车充电器的滤波器设计，具有较佳的综合输出特性。

2.5 实验验证

论文如图1所示，在实验室环境下建立了简单的电池充电系统。电源电压经9kW调压器降压后由相控整流桥转换为直流，经滤波器滤波后给三节串联的电池充电。每节电池端电压为12V，内阻约为0.2Ω。调压器输出电压为55V.当 α=40°时充电电流如图7所示。

图7 三种滤波器输出电流

实验验证了仿真的结论。阻尼控制法暂态响应时间最短，但是稳态滤波效果可调范围较窄;而极点分析法虽然响应速度略慢，但是有较宽的输出可调范围。因此更适用于电池这样内阻小，具有反电动势的等容性负载。

3 结论

论文针对动力蓄电池组对充电器的特殊要求和电池组自身的特殊性，讨论了电动汽车充电器直流滤波器的设计方法。通过对滤波器匹配型和传输特性的比较，确定了减少电流纹波的非匹配型切比雪夫滤波器的算法;通过对谐振法、阻尼控制法和极点分析法的综合比较，确定了提高快速响应的修正方法。并通过仿真和实验验证了方案的合理性和可行性。

［1］ 胡明辉，秦大同，舒红.混合动力汽车蓄电池的快速充电方法［J］.重庆大学报(自然科学版).2004，27(11):1－3.

［2］ 王丙元，高精度大功率稳流电源系统的研究［D］.天津大学，2002，5.

［3］ 李俄收，吴文民.电动汽车蓄电池充电对电力系统的影响及对策［J］.华东电力，2010(1):109－113.

［4］ 王兆安，杨君，刘进军，等，谐波抑制和无功功率补偿［M］.北京:机械工业出版社，2004.

［5］ 徐曼珍.新型蓄电池原理与应用［M］.北京，人民邮电出版社，2005.

［6］ 张丽霞，李和明，等.切比雪夫滤波器在动力蓄电池组检测中的应用［J］.电工技术学报，2008，23(3):137－142.

［7］ 黄席椿，高顺泉.滤波器综合法设计原理［M］.北京:人民邮电出版社1978.

［8］ Kang Wei，Wang ping，et al.Research on the Matched DC Filter Design in the Power Accumulator Battery Testing System［C］.ICECE 2010，Wuhan，China.

［9］ Zhang Lixia，Yan Xiangwu，et al.Design and Simulation of Fast-Response Filter Based on Locomotive Battery Testing System［C］.EPEPEMC 2006，Portoroz，Slovenia.

［10］ Yan Xiang-wu，Zhang Li-xia，et al.LC Filter Parameter Design for the Bidirectional Converter［C］，SPEEDAM2006，Taormina(Sicily)-ITALY，2006:23－26.

［11］ 陈道炼，胡育文.低损耗可控阻尼两级LC输入滤波器设计与仿真［J］.电工技术学报.2001，2:43－47.

［12］ 李和明，张丽霞，等.动力蓄电池组测试系统中双向直流滤波器设计［J］.中国电机工程学报.2009，9:1－7.