基于DFIG风电并网的VSC-HVDC电压稳定性分析

张明光 张彦凯 赵金亮 刘进文

(1.兰州理工大学 电信学院，甘肃 兰州 730050;2甘肃省第一建设集团责任有限公司安装工程公司甘肃 兰州 730050)

0 引言

我国的风电场大多使用固定转速的风电机组，所以电压稳定性问题是其运行中普遍出现的问题。随着大容量风电场的并网，电压稳定性问题日益突出，出现了导致母线电压崩溃的现象。所以在风电并网的发展中，基于双馈感应发电机(doubly fed induction generator，DFIG)的变速风电机组具有发电效率高、原动机损伤小、改善电能质量、能实现最大风能捕捉并减小机械部件所受应力等优点，有着很大的发展前景［1－2］。文中采用基于绝缘栅双极晶体管(insulated-gate bipolar transistor，IGBT)的VSC-HVDC 系统连接DFIG和电网。VSC-HVDC的2个换流站可以独立控制两侧的无功，连接DFIG的换流站同时能够控制交流电压的幅值和频率，而且DFIG不需改变控制策略就能实现最大功率追踪。VSC-HVDC系统采用的是全控型开关器件，使得控制更快捷更稳定，同时有效地降低了谐波含量［3－4］。

在现有的风电并网中，解决电压稳定性问题的方法主要有:无功补偿和无功的合理分配;带负荷调压变压器调压;适当增大导线直径和装设并联电抗器等［5］。目前，正常控制策略下的大部分双馈风电机组控制系统在网侧发生大扰动故障时，无法提供动态电压支持，另外由于故障线路切除，导致电网结构更弱，机端电压降低。因此，有必要改善基于DFIG并网风电场暂态电压稳定性的措施。对风电并网所引起的电压稳定性问题，通常是在母线上安装电容器组用以补偿无功需求。但当风速变化或系统运行方式改变时，风电场的母线电压会出现较大的波动，固定电容器组的投切不能使电压维持在允许的范围内。使用快速投切电容器组则能很好地解决这个问题，但此时要明确电容器的总容量、分组容量以及投切规则。

1 VSC-HVDC系统结构

基于DFIG的VSC-HVDC系统连接电网的系统结构如图1所示。S1，S2是VSC-HVDC系统的两个变流器;S3和S4，S5和S6分别是2个DFIG的双向变频单元。DFIG定子侧与SVCHVDC的变流器相连，转子侧通过双向变频功率单元(S3和S4，S5和S6)也连接到S2变流器上。

图1 VSC-HVDC连接DFIG和电网的系统结构

2 基于DFIG的风电机组模型

2.1 空气动力学模型

风力发电机组的空气动力学模型为公式1所示［6－9］

式中:PM为风电机组从风中获取的能量转化成的风电机组机械效率;ρ为空气密度;R为风力机叶轮半径;λ为叶尖速比;β为桨距角;CP为叶片的风能转换效率系数，是λ与β的函数，改变λ与β可以改变CP的值;VW为风速。

2.2 DFIG模型与功率控制

根据电机数学模型，利用帕克(Park)变换一般化d，q坐标系下电机模型的有名值电压方程、磁链方程、转矩方程、功率方程分别为(4)式、(5)式、(6)式、(8)式所示。为使变换前后功率守恒，其变换矩阵应为正交矩阵，即此变换应为正交变换;而如果变换矩阵为复数矩阵，则应为酉矩阵。观察帕克变换矩阵，如取

则P－1=PT，则变换前后的功率就可守恒。由［10］

令

其中公式4～7中 u、i、ψ 为绕组的电压、电流、磁链;ω1、ω2为定子、转子旋转角速度;Ls、Lr分别为定子绕组与转子绕组的自感;Ln为定子绕组与转子绕组之间的互感;下标s、r分别代表电机的定子与转子;下标d、q分别表示电机的的d、q轴。在不计定子损耗的条件下，定子侧发到电网上的有功和无功Ps、Qs为(8)式所示。

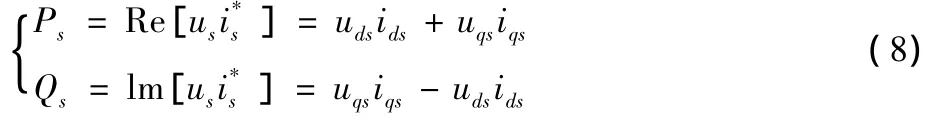
如果变换矩阵中的系数是2/3，则(6)、(8)左侧分别乘以3/2，以保证与原三相系统等效。

在电力系统的稳定性研究中，一般都不计网络的电磁暂态过程，因此本文的DFIG定子磁链暂态过程也能忽略，因为定子电阻的压降远远小于定子的端电压，所以定子电阻上的压降也可忽略。为了能实现对公式(8)中DFIG的有功、无功解耦控制，同时为了能在MATLAB/Simulink仿真软件中方便的实现，将同步旋转的d轴与定子电压矢量方向重合，所以有uds=Us，uqs=0。在上述假设条件可行的情况下，DFIG的定子轴的有功功率、无功功率能够表示为

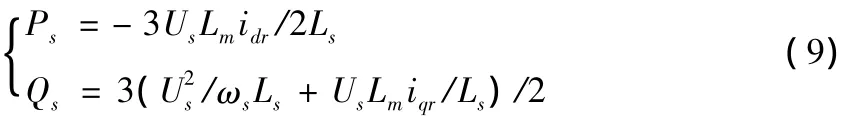
其中，转子绕组的有功电流分量idr能够实现对定子绕组有功功率Ps的控制，转子绕组无功电流分量iqr可控制定子绕组的无功功率Qs;idr、iqr为转子电流在以定子电压矢量方向的同步旋转坐标系d轴、q轴上的分量，而idr、iqr之间不存在耦合关系，从而实现了对定子绕组有功功率Ps和无功功率Qs的解耦控制。

间接控制变流器加在转子绕组上的外加电压可以实现对转子电流的控制，由上述公式结合DFIG的特点，可推导出用转子外加电压控制转子电流的控制方程式(10)，式中:s表示电机的转差率;Rr为转子绕组的电阻;ωs表示同步转速;其中

在定子电压定向坐标下，转子有功、无功电流是完全解耦的，但相应的控制电压矢量没有完全解耦，如果采用udr控制idr，用uqr控制 iqr，则需要分别增加前馈输入－sωsλLriqr+sLmUs/Ls与sωsλLridr，便可以完全实现电压的解耦控制。

2.3 DFIG的简化电路模型

风力发电机组采用双馈异步电机通过将机械能转化为电能，并输出有功功率，同时从电网中吸收无功功率来建立磁场，在潮流计算中不能简单的把风电机组视为PQ节点或PV节点，应该根据风电的特点建立合理的潮流模型，文本将滑差作为状态变量。DFIG的电路模型如图2所示。

图2 异步发电机的等效电路

在图2中Rr+jXr为转子阻抗，Rs+jXs为定子阻抗，Xm为励磁电抗，S为滑差上的功率Pr为风力机输送到异步电机转子上的机械功率Pm，将图2中aa'右侧的电路简化为等效电路如图3所示。

图3 简化右侧电路后的等效电路

图3中Re(s)+jXe(s)为aa'右侧的等效阻抗，其表达式为

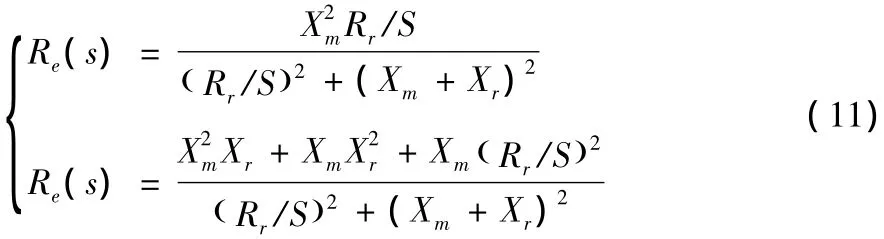
图3中风电机组输出系统功率的表达式为。

将图2中bb'左侧电路化为等效电路如图4所示。

图4 简化bb'左侧电路后的等效电路

图4中R1+jX1为bb＇左侧等效阻抗，其表达式

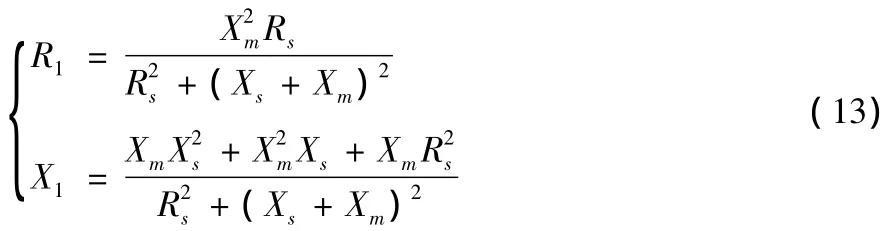
由图4可以得到发电机转子功率表达式为

在含有风电机组的配电网潮流计算中，一般情况下风电机组可以视为PQ负荷节点，其中PLi，QLi为第i点的负荷有功与无功，则节点i的潮流计算方程为

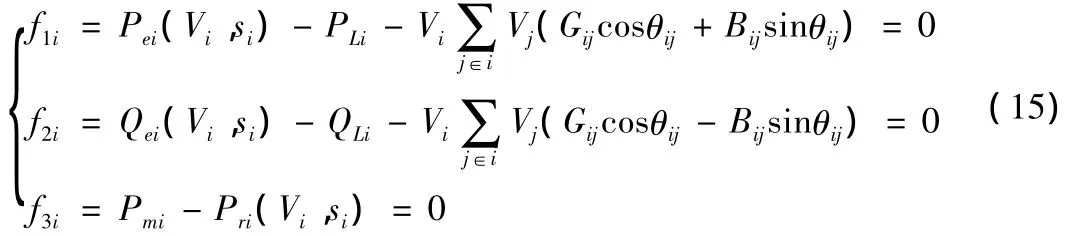
3 电压源型变流器数学模型

电压源型变流器中，大多采用半桥或者全桥结构。本文以图5所示的全桥为例进行分析。以电感电流iL和电容电压uC为状态变量，逆变桥中点输出电压uS和输出电流i0为输入变量，系统时域下的状态方程可列写为

图5 单项全桥逆变电路

经过拉式变换，可得到频域下uC的表达式

式中负载电流i0可视为外界对系统的扰动，当系统空载时，有

4 风电场无功电压特性

风电机组安装无功补偿设备时，根据风电机组容量和型号的区别，风电机组无功补偿设备的容量和投切规则不同，但都遵循以基本的原则，那就是根据风电机组的有功出力确定投切的无功补偿容量。如图6所示。为一个600 kW风电机组的功率特性，其无功补偿设备为5组容量各为50 kvar的电容器组，其投切规则为当有功功率低于额定容量的40%时，投入4组，当有功功率大于额定容量的40%时，5组全部投入。

图6 DFIG的功率特性曲线

由图6的异步电机组的功率特性曲线可以看出，

(1)当风电机组的有功功率较小时，功率因数变化较大，而此时无功功率变化较为平稳。

(2)当风电机组的有功功率增加到一定值时，全部投入无功补偿设备，此时功率因数近似于一恒定值，有功与无功之间也近似于线性关系。

5 确定无功补偿容量

5.1 SVC 模型

根据母线电压的变化量来确定无功补偿容量，并且用潮流计算作为计算工具。用无功补偿度来表示电网的无功补偿水平，其表达式如式(19)所示

其中Wa(Wa≥0.7)表示无功补偿度;Qc表示容性无功补偿容量;Pn表示装机容量。因分电机组的原额定功率因数低，一般要在风电机组的出口并联补偿电容，以保证功率0.97≤cosφ≤1，则系统的功率因数如公式(20)所示

其中S表示风电场的容量;Qc1表示线路容性充电功率;Qc2表示无功源;P1、Q1分别表示补偿前的风电场有功与无功，则S=P1－jQ1，所以补偿容量如式21所示

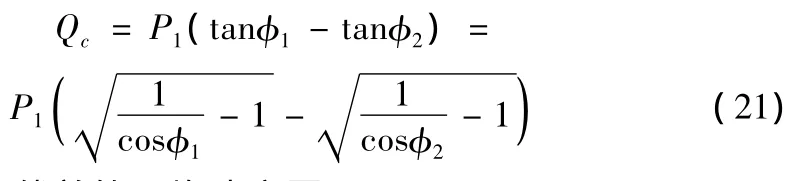
其中cosφ1为补偿前的平均功率因数;cosφ2为补偿后的平均功率因数。

为了提高风电机组的功率因数，通常在风电机组的机端并联一定的可投切电容器。考虑到风电无功需求的特性。多采用静态与动态混合的补偿方式。带有固定电容器(Fixed capacitors，FC)的 TCR(Thyristor controlledReactor)型静止无功补偿器(SVC Static Var Compensator)是典型的代表，它可以快速平滑地调节无功补偿功率的大小，提供动态的电压支撑，使系统的运行性能得到改善。带有FC的TCR型SVC的原理如图7所示:

图7 带有FC的TCR型SVC

SVC通过控制双向并联的晶闸管触发相位角，能够控制电感接入系统时每个周波的时间，最终控制SVC的视在电抗。SVC的视在电抗表达式为

x表示SVC的视在的电抗;xt表示SVC的可控电抗;xc表示电容C的等效电抗，xc=－1/ωC。同时可控电抗xt与触发角α的关系式为

其中 xL=ωL。需要 SVC感性和容性双向的调节，则取xL=－1/2xC，因 α∈［1/2π，π］时，xt是 α 的单调增函数，所以当α=1/2π 时，xt有最小值－1/2xC，x有最大值－xC;当 α=π 时，xt有最大值，xt→∞，x有最小值 xC。所以 x∈［xC，－xC］。

晶闸管的触发控制决定了系统中出现的等值并联导纳，因而SVC的动态数学模型能表示为

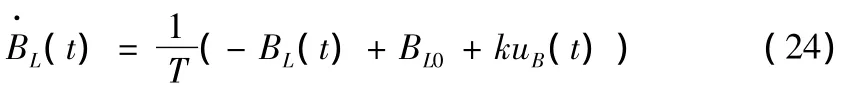
其中，T为SVC的时间常数;BL(t)为SVC的电感支路导纳;BL0为BL(t)的初始值;k为SVC控制器增益;uB(t)为控制器的输入。

5.2 SVC控制策略

在图7中，为了维持SVC的母线电压，建立微分方程

其中，ΔU(t)=U(t)－U0，U0为 SVC母线的工作点的电压值;IB(t)为SVC电抗器的电流;d(t)为外部随机扰动。而x1和x2为图8中的AC和BC之间的等效电抗。

图8是输电线路中间装有可连续调节的SVC补偿装置的三母线简化系统图。

图8 三母线系统的等效简化图

图8中，UA和UB分别为母线A和母线B的电压;δA和δB为母线A和B对应电压的角度;U和δ为SVC母线电压和对应的角度。

图7中的SVC控制系统原理如图9所示。

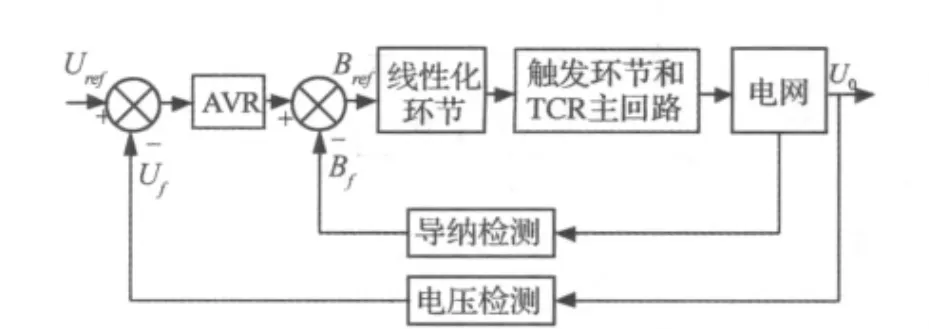
图9 SVC控制原理图

根据控制目的，要维持电压值的恒定，必须引入电压闭环控制。而本文在单电压闭环的基础上又引入了导纳闭环系统作为内环，目的就是在负载扰动时可以改善系统的性能。电压外环的作用主要是为了获得一个良好的稳态性能，其调节器采用PI控制，实现电压的无静差跟踪。控制目的是:能够控制母线电压为给定值，同时能够使系统的功率因数≥0.95。

6 仿真分析

为了验证本文所提出的SVC能够对风电场电压稳定和提高系统运行性能方面的良好作用，通过MATLAB/Simulink仿真软件对图1所示的有源型VSC-HVDC系统行进了仿真分析。单机组的参数如表1所示。

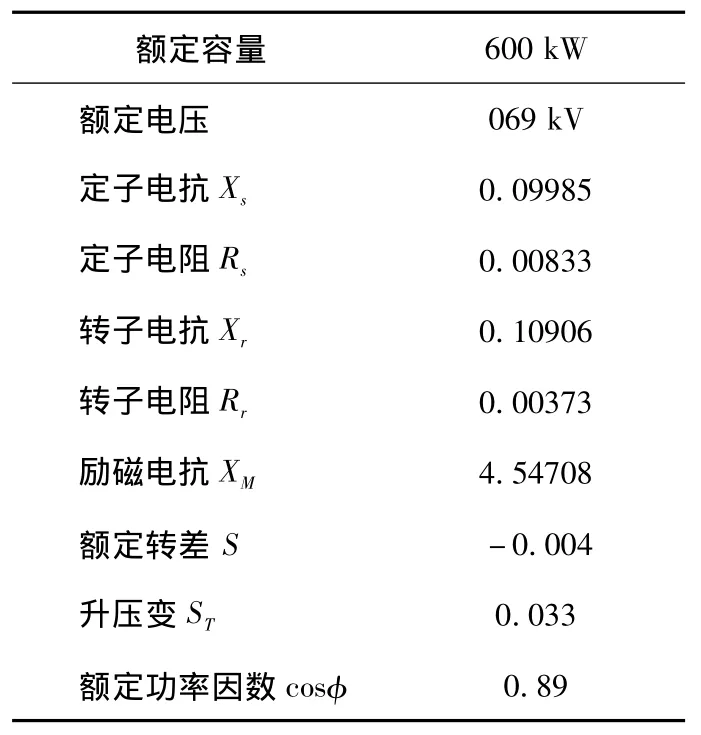
表1 单台异步电机参数

风电场所用的DFIG机组的额定容量为600kW，在风电场变电站低压端接入30Mvar的SVC，利用仿真软件MATLAB/Simulink对VSC-HVDC系统在阵风作用下以及风场出口处发生三相短路时电压，功率的变化情况分别进行了仿真。

从图10仿真结果可得出，当安装了SVC以后，风电场的节点电压波动明显降低了，这说明了SVC可以显著地稳定风电场的电压。

图10 阵风下风电有功功率和电压曲线

从图11的结果可以读出，故障切除时间为100ms的仿真过程中，在加快故障切除后节点电压恢复和提高系统稳定性方面，体现了SVC的无功调节能力。

图11 短路故障后风电有功功率和电压曲线

7 结论

对改善基于双馈感应电机的VSC－HVDC系统并网的风电场电压稳定性问题进行了研究及仿真。将SVC安装在风电场出口，根据风电场接入点的电压波动量来控制SVC无功补偿量，可以稳定风电场的电压，降低风电功率波动对网侧电压的影响。通过含风电场的Simulink仿真计算验证了SVC的有效性以及其对风电场及网侧电压稳定性的贡献，确保了风电机组的电压稳定及电网的安全。

［1］ ZINGER DS，Muljadi E.Annualized wind energy improvement using variable speeds［J］.IEEE Trans on Industry Applications，1997，33(6):1444－1447.

［2］ DATTA R，Ranganathan VT.A method of tracking the peak power points for variable speed wind energy conversion system［J］.IEEE Trans on Energy Conversion，2003，18(1):163－168.

［3］ 陈谦，唐国庆，胡铭.采用dqo坐标的SVC-HVDC静态模型与控制器设计［J］.电力系统自动化，2004，28(16):61－65.

［4］ 李庚银，吕鹏飞，李广凯，等.轻型高压直流输电技术的发展与展望［J］.电力系统自动化，2003，27(4):77－80.

［5］ 苑舜，韩水.配电网无功优化及无功补偿装［M］.北京:中国电力出版社，2003，8.

［6］ POLLER M，ACHILLES S，MOODLEY G.Variable-speed wind genera tor models for power system stability analysis［C］.The world wind Energy Conference andRenewable Energy Exhibition，Capa Town，South Africa，2003.

［7］ AKHMATOV V.Analysis of dynamic behavior of electric power systems with large amount of wind power［D］.Copenhagen:Technical Univer-Sity of Denmark，2003.

［8］ 吴学光，张学成，印永华，等.异步风力发电系统动态稳定性分析的数学模型及其应用［J］.电网技术，1998，22(6):68－72.

［9］ POLLER M. Doubly-fed induction machine models for stability assessment of wind farms［C］.IEEE-Power-Tech Conference，Bologna，Italy，2003.

［10］ KUNNDER P.Power system stability and control［M］.New York，NY，USA:McGraw-Hill，1994.