ZVZCS全桥变换器模型分析及控制系统设计

张宁云 程善美

(华中科技大学 控制科学与工程系，湖北 武汉 430074)

0 引言

全桥变换器拓扑是目前国内DC－DC变换器中最常用的电路拓扑之一，在中、大功率应用场合更是首选拓扑，而在很多应用场合对其性能都有较高的要求，包括效率、电磁干扰、功率密度和可靠性等。提高开关频率无疑是提高性能最为直接有效的手段。但开关频率增大意味着开关损耗的增大，为解决这一矛盾，软开关技术应运而生。

全桥变换器的软开关拓扑结构有很多种，大体都是在原有的拓扑上增加一些辅助的电路［1－3］，本文详细介绍了一种结构最为简单的零电压零电流全桥变换器的结构［4］，分析了其工作原理，并建立其小信号数学模型，同时给出了基于小信号数学模型设计的电压电流双闭环控制方案。

1 电路拓扑结构及工作模式分析

图1和图2分别是ZVZCS变换器的电路主拓扑结构及主要的电压、电流波形。其中G1、G3组成超前桥臂，在开通和关断时处于零电压的状态，G2、G4构成滞后桥臂，在开通和关断时处于零电流的状态。

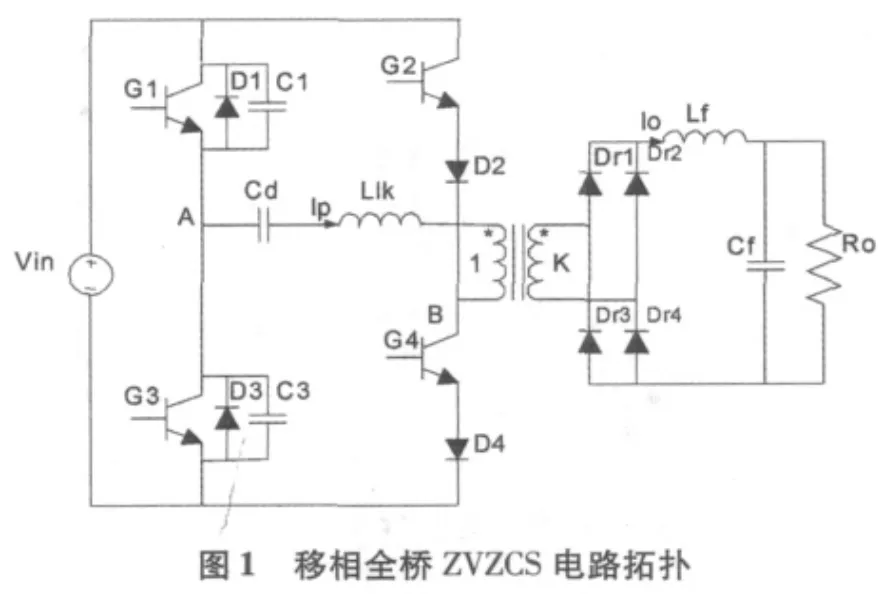
按照时间段该变换器的工作过程分为6种工作模式，如图3所示。选定开关管G1的关断时刻为分析的起点，各工作模式分别简述如下。在分析中，假设:功率器件IGBT为理想开关;二极管为理想二极管;电容和电感均为理想器件;忽略电路中的损耗;变换器工作在滤波电感电流连续模式下(CCM)。图3中以带箭头的粗实线表示电路中的电流方向。

图3 ZVZCS移相全桥变换器工作模式分析

(1)工作模式0(t＜t0)

如图3(a)所示，G1、G4导通，电容Cd电压线性上升。

(2)工作模式1(t0＜t＜t1)

如图3(b)所示，G1关断，由于电容C1的作用，G1零电压关断，由于副边滤波电感Lf的值很大，变压器原边电流大小、方向都不变。电容C1充电，C3放电，电容Cd继续充电，变压器原边电压VAB的值逐渐减小。C3电压降为零时D3导通，工作模式1结束。

(3)工作模式2(t1＜t＜t2)

如图3(c)所示，电容C1的电压值达到电源电压，电容C3的电压值减小至0，G3零电压开通。电容Cd充电至最大值VCdp。原边电流通过二极管D3续流并开始逐渐减小。当原边电流下降到零时，工作模式2结束。

(4)工作模式3(t2＜t＜t3)

如图3(d)所示，原边电流为0，电容Cd保持最大电压值不变，G4零电流关断。

(5)工作模式4(t3＜t＜t4)

如图3(e)所示，G2零电流开通，原边电流反向增大。变压器副边绕组被短路，四个整流二极管导通续流。

(6)工作模式5(t4＜t＜t5)

如图3(f)所示，变压器开始工作，电容C4继续放电。

(7)工作模式6(t5＜t＜t6)

工作模式6与工作模式1相类似，在工作模式6结束时，电容Cd的电压达到反向最大值。

2 移相全桥ZVZCS变换器小信号模型分析

由于功率器件的非线性导致其构成的变换器也是非线性的，为了得到变换器的数学模型，需要对其做线性化处理，这里应用常用的小信号模型分析法来建立移相全桥变换器的模型［5，6］。认为:当变换器工作在稳态时，其电压和电流由稳定的直流分量和小信号的交流分量叠加构成［7］。移相全桥ZVZCS变换器是由BUCK电路衍生而来的，可借鉴BUCK电路的分析方法［8］，本文中只讨论滤波电感电流连续的情况。从以上分析可知在工作中出现了变压器副边绕组短路的情况，所以副边得到的有效占空比小于原边占空比，称为占空比丢失，由图2可知副边得到的有效占空比为

其中:T35=t5－t3，T34=t4－t3，T56=t6－t5，C1=C2=Cr，K 为变压器变比。

由上式可知，当电路结构确定后，变压器变比K、漏感 Llk、电容Cr都是固定不变的，并且电路的开关频率也是固定不变的，所以有效占空比可以写为原边占空比D、副边电感电流I0、输入电压Vin的函数，即

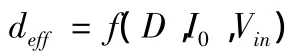
将上式在稳态工作点(D，I0，Vin)处展开为Taylor级数，并略去二次及以上高阶分量得到

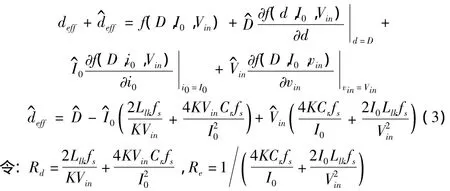
上式可简化为

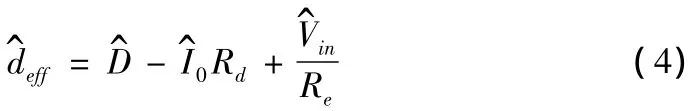
变压器副边传递函数为

BUCK电路滤波电感电流连续模式(CCM)小信号模型如图4所示。

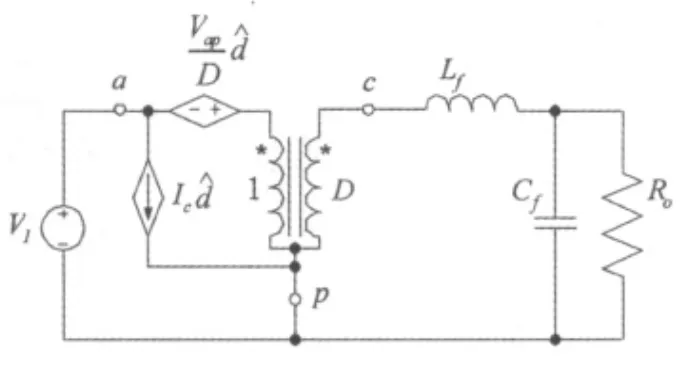
图4 BUCK电路小信号模型

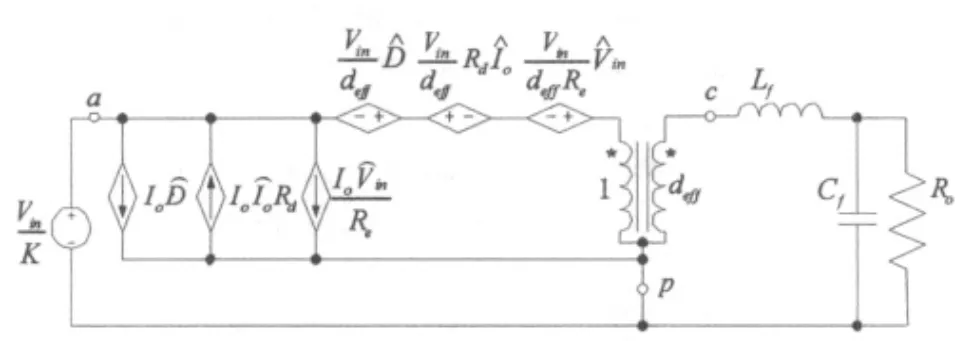
图5 移相全桥ZVZCS小信号模型

3 移相全桥ZVZCS变换器控制系统设计及仿真结果

电压环控制具有稳态性能好的优点，但不能保证变换器在负载突变时快速的响应，而电流控制则可以改善变换器的动态性能，结合这两种方法，移相全桥ZVZCS变换器采用输出电流和输出电压的双闭环控制系统，其结构框图如图6所示。

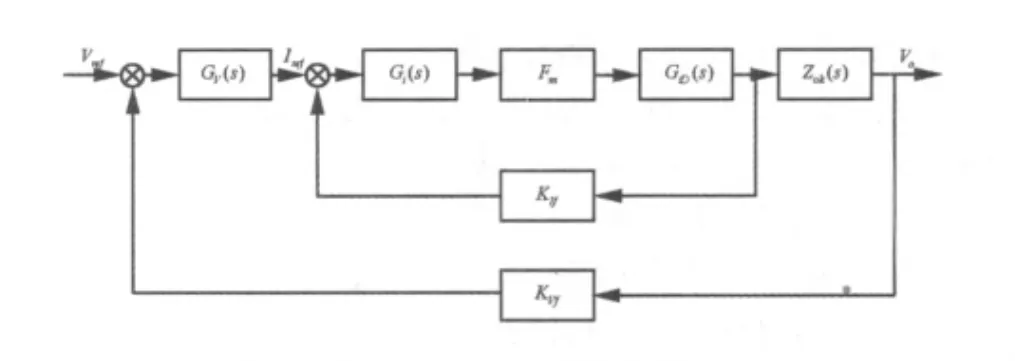
图6 移相全桥ZVZCS变换器双闭环控制系统

其中Gi(s)为电流环控制器传递函数，采用PI型控制器，GV(s)为电压环控制器传递函数，采用PI型控制器，Fm为比较环节增益，Zok(s)为负载与滤波电容的并联阻抗。

电流环闭环传递函数为

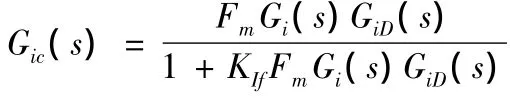
系统开环传递函数为

电路参数为:Vin=1500VDC，fd=10kHz，Cr=3.3×10－8F，Cd=1.1 ×10－5F，Llk=5 ×10－6H，Cf=1.02 ×10－2F，Lf=8 ×10－4H，R0=3.6Ω，V0=600VDC，变压器变比 K=4∶3。

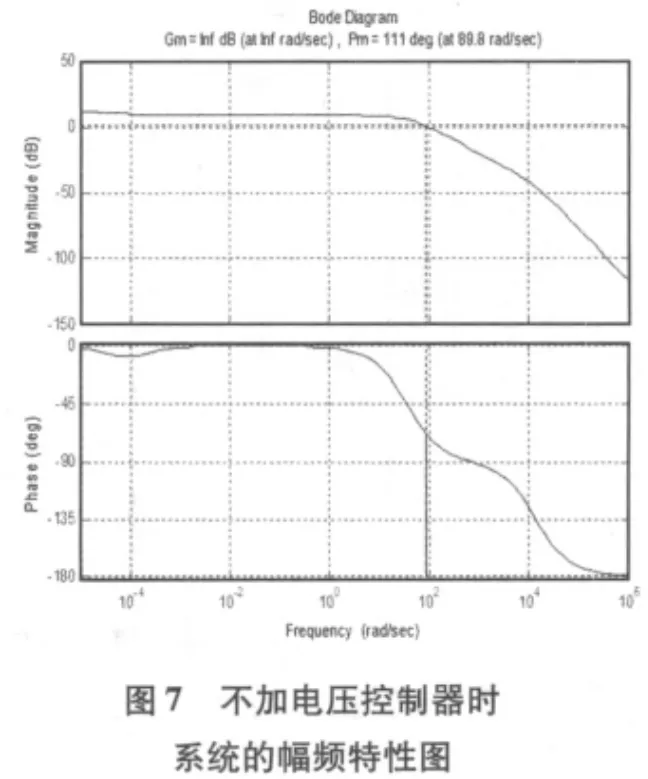
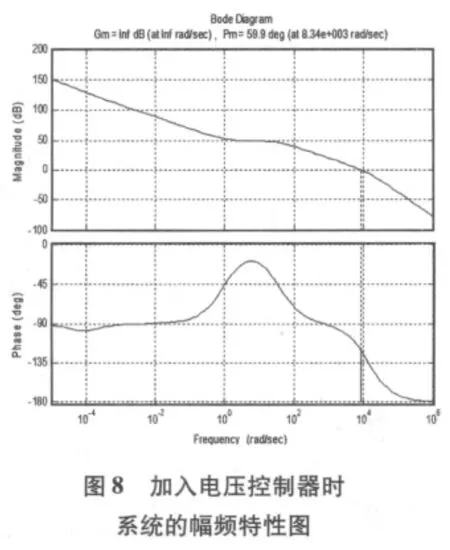
不加电压控制器时系统的开环幅频特性如图7所示，系统幅值裕度无穷大，相角裕度 111°，截止 频 率 14.3Hz，截止频率较低，系统的动态性能较差，当加入电压控制器后系统的开环幅频特性如图8所示，系统幅值裕度无穷大，相角裕度 59.9°，截止频率1.33kHz，截止频率的提高有效的改善了系统的动态性能。

在 MATLAB/SIMULINK仿真环境下搭建全桥变换器双闭环控制系统的仿真平台，实验结果如图9～图13所示。(注:在图12与图13中，为清晰地分辨超前桥臂与滞后桥臂的软开关效果，分别将IGBT驱动波形的幅值放大了1000倍和100倍)。

变换器带额定100kW纯阻性负载，在启动后经历约0.01s达到稳定，超调约为10V左右，在稳定工作阶段，输出电压正负波动在1V之内，如图9所示。

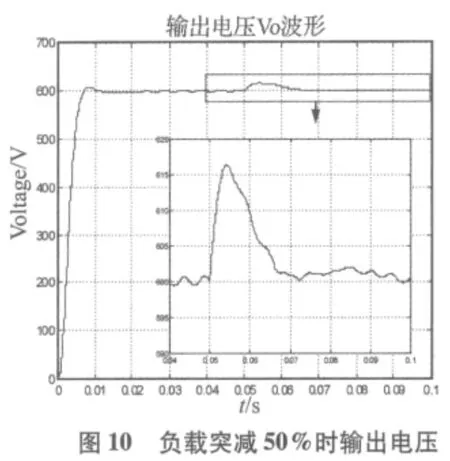
图10所示在0.05s时负载突减50%，变换器输出电压升高17V左右，在经历0.02s之后输出电压恢复正常值。图11所示在0.05s时负载突加100%，变换器输出电压降低30V，经历0.03s之后输出电压恢复正常值。

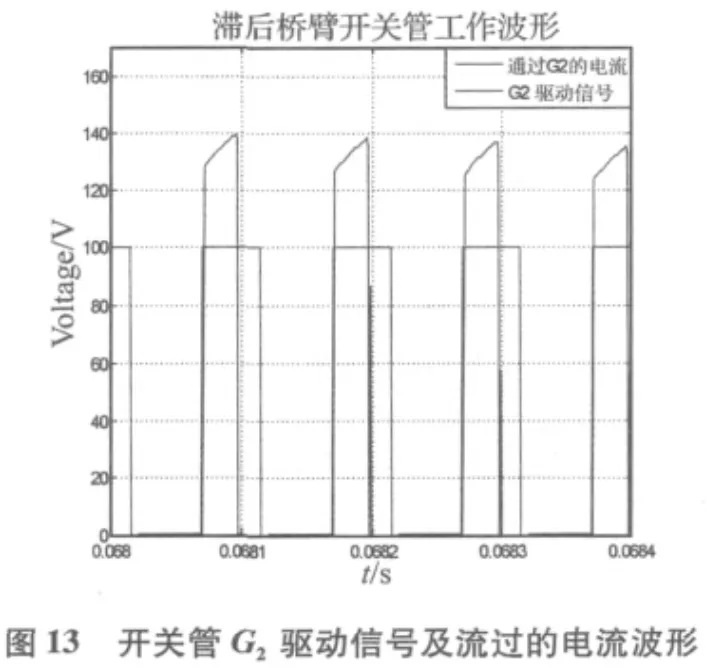
从图12中可以看出超前桥臂开关管G1在开通和关断的过程中都处于零电压的状态，而图13则证实了滞后桥臂开关管G2在开通和关断的过程中都处于零电流的状态，整个变换器实现了软开关工作。

4 结论

本文详细介绍了滞后桥臂串联二极管的零电压零电流全桥变换器的结构，分析了其工作原理，并在小信号数学模型的基础上建立了电压电流双环控制方案，从仿真的实验结果可以看出，该变换器拓扑能够实现开关管的软开关工作，应用文中提出的双闭环控制策略，变换器具有响应速率快，系统性能稳定的优点。

［1］ Jung-Goo Cho，Ju-Won Baek Jeong，Chang-Yong，et al.Novel Zero-Voltage and Zero-Current-Switching Full-Bridge PWM Converter Using a Simple Auxiliary Circuit［J］. IEEE Transactions on Industry Applications，1999，35(1):15－20.

［2］ Jung-Goo Cho，Ju-Won Baek，Chang-Yong Jeong，et al.Novel Zero-Voltage and Zero-Current-Switching Full Bridge PWM Converter Using Transformer Auxiliary Winding［J］.IEEE Transcations on Power Electronics，2000，15(2):250－257.

［3］ Eun-Soo Kim，Kim Y.A ZVZCS PWM FB DC/DC Converter Using a Modified Energy-Recovery Snubber［J］.IEEE Transactions on Industrial Electronics，2002，49(5):1120－1127.

［4］ Xinbo Ruan，Yan Y.A Novel Zero-Voltage and Zero-Current-Switching PWM Full-Bridge Converter Using Two Diodes in Series With the Lagging Leg［J］.IEEE Transactions on Industrial Electronics，2001，48(4):777－785.

［5］ Tiecheng S，Peng G，Hongpeng L.Equivalent switching modeling of ZVZCS FB PWM converter［C］//Systems and Control in Aerospace and Astronautics，2006:268－272.

［6］ TINGTING S，NIANCI H，LOINOVICI A.DC and small-signal analysis，and design of a novel ZVZCS three-level converter with reducedRectifier voltage stress［C］//Power Electronics Specialists Conference，2004.PESC，2004:4093－4099.

［7］ ERICKSON R W，Fundamentals of Power Electronics［M］.New York:Chapman and Hall，1997.

［8］ Application Report:Understanding BUCK Power Stages in Switch mode Power Supplies［R］.TI Literature Number SLVA057.